基于Levenberg-Marquardt算法的COVID-19预测研究分析

杨振民 孙燕 代忠豪 王深龙 苏金萍 李悦熙薇

摘  要：2019年12月，武汉市部分医疗机构陆续出现不明原因肺炎病人。武汉市持续开展流感及相关疾病监测，发现病毒性肺炎病例27例，均诊断为病毒性肺炎及肺部感染。至此，一种被世界卫生组织命名为2019-nCOV的全新的冠状病毒出现在人类的视野中。2020年3月12 日，世界衛生组织宣布，席卷全球的冠状病毒引发的病毒性肺炎（COVID-19）是一种大流行病。迄今为止，全球已有超过200个国家/地区报告了新型冠状病毒感染病例，且存在很多无症状感染患者。因此，对疫情的防控以及准确快速的发现无症状感染者的研究是非常有意义和必要的。

从人类发展到如今，流行病出现了很多次，但被世卫组织评为大流行病的只有2009年的H1N1以及如今COVID-19。我们根据近20年来影响力较大的4种传染病SARS、MERS、H1N1、COVID-19数据来作为界定“流行”与“大流行”的标准。首先对数据进行预处理，根据题中所给的指标进行定量分析，选出影响力较大的因子，之后通过BP神经网络模型对数据进行归一化处理，做出该数据序列未来发展趋势，根据最终输出的结果进行界定。

根据指标分析定性的去设计病毒检测抽样方案，对无症状感染者进行分布预测，我们可以对数据进行描述性分析，由于传染的过程需要时间，传染过程也需要一定的概率，为提高模型预测的准确性，本部分增加了更多的考量变量，同时采用精度更高的，基于遗传算法的神经网络模型，将整理后的数据集中，80%的数据用于模型求解，以确定变量指标的权值与阈值，将剩余的20%的数据通过残差计算用于模型精度检验。为进一步提高模型精度与计算效率，提出采用基于Levenberg-Marquardt算法求解。

关键词：新型冠状病毒;BP神经网络;遗传算法;Levenberg-Marquardt算法

1引言

国家卫生健康委决定将新型冠状病毒感染的肺炎纳入法定传染病乙类管理，采取甲类传染病的预防、控制措施。截至2020年1月7日21时，实验室检出一种新型冠状病毒。1月20日，习近平对新型冠状病毒感染的肺炎疫情作出重要指示，强调要把人民群众生命安全和身体健康放在第一位，坚决遏制疫情蔓延势头。2020年1月30日，世卫组织发布新型冠状病毒感染肺炎疫情为国际关注的突发公共卫生事件，强调不建议实施旅行和贸易限制。

主要症状感染病毒的人会出现程度不同的症状，有的只是发烧或轻微咳嗽，有的会发展为肺炎，有的则更为严重甚至死亡。该病毒致死率约为2%到4%，但这是一个非常早期的百分比，随着更多信息的获得可能会改变。同时，这并不意味着它不严重，只是说病毒感染者不一定人人都会面临最严重的后果。

2数据预处理

本研究的数据资料来自于国家卫健委及世界卫生组织发布的流行病疫情报告数据（截止到2020年4月15日）。

首先对这些数据进行预处理，依次排列，形成具有120个元素的全球单日报告发病率序列，计算公式为单日发病率=单日发病数/年均人口数*100000/100000.

3 BP神经网络模型的构建

在构建的BP神经网络模型中，假定神经网络中输入层为8个神经元，分别为人口数、感染数量、病死人数、疫情时间、经济状况、医疗条件、人口密度、防疫政策，隐含层为31个神经元，输出层为2个神经元，分为;流行和大流行。

4图标结果

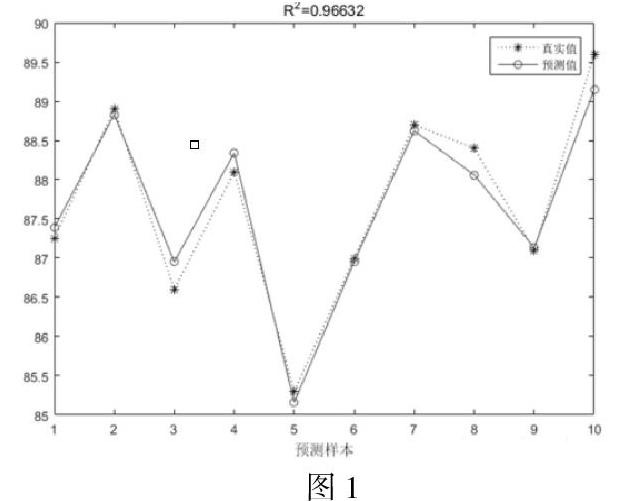
在对建立的神经网络模型进行调整以后，得到的神经网络回归图形。此时得到的权值和阈值是本神经网络模型在当前精度下的各层级之间的关系值，通过层级之间的权值和阈值，可以将剩下的20%的数据进行预测，同时检验本模型的精度。然后对训练后得到的10组结果进行反归一化后，再计算出结果与标准结果的相对误差，画出10组测试集所得出的结果与答案的相对误差的柱形图。从图中我们可以看出训练得到的结果是比较准确的，相对误差最大只为0.6%。然后再计算出决定系数，决定系数也称为拟合优度，决定系数越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。决定系数的范围在[0，1]之内，越接近1代表相关性越高，越接近0代表相关性越低。本次训练得到的模型计算出的结果的决定系数为0.966，可以很好的对结果进行预测。

最后画出真实结果与使用BP神经网络预测结果的对比图，从图1中我们可以看出，预测的结果与实际的结果是十分相近的，说明该模型具有较好的回归结果。

由上述可以得出流行病与大流行病的的标准在于万人感染数以及万人死亡数量与时间的关系，由此，我们可以得到中国疫情感染率为0.05/万人，死亡率为0.927%，湖北省死亡率为5.48%，基于政府管控干预下，其实际真实死亡率为0.762%;全球新冠肺炎传播增长时间已达到63天，感染率为2.86/万人，死亡率为6.572%，感染超过200个国家/地区。

SARS在全球传播增长时间为73天，其感染率为0.012/万人，死亡率为10.91%;MERS在全球感染率0.0016/万人，死亡率为37.8%;H1NI流感全球传播增长时间为146天，由于后期不在统计确诊率，因此通过模型估计判断出其感染率为2.14/万人，死亡率为1.34%。对最终数据进行分析，可以得到判断超过0.68/万人，死亡率高于1%，传播增长时间超过3个月，即界定为大流行病。

5 NSIR模型和动力学分析

含无症状带毒者的NSIR模型中，总人口被分成4种状态.  ，和R分别代表易感染者、感染者，无症状感染者（无症状带毒者），和恢复者（感染并治愈者和感染后无症状并自愈者）在时刻的t数量. 这4种状态之间的疾病传播流程图见下图，其中 。

首先感染者I和无症状带毒者 以 的几率传染未感染者S，使其成为发病感染者;以 的几率使其成为无症状感染者. 感染者I的痊愈率为 ，无症状带毒者恢复正常的速率为 . 易感染者的自然增长率为 ，无症状带毒者的自然增长率为 . 未感染者，无症状带毒者和恢复者的死亡率为 ，感染者的死亡率为 . 其中所有的参数都是正数.

实际上我们可以假设无症状带毒群体自愈的速度 高于感染者群体的康复速度 ，从而可推出不等式成立.

该定理的生物学意义是：如果方程中的参数满足上述不等式，则在新型病毒的感染的初期不会引起新型病毒的传播而自然消失，否則新型病毒将扩散传播。可以将其改写为：

可称 为增长指数. 由上式可以看出感染速率 和 都较低，则初期感染不会引起该传染病的传播而自然消失. 而 是易感者被感染成无症状带毒者的速率，由于无症状带毒者难于防控，因此 在流行病传播中也扮演着重要的角色.

因此新增感染的持续说明现行防控措施对有症状感染和/或无症状感染的阻断还需加强。

6中国四川新型冠状病毒疫情的模拟与预测

有关四川疫情的诸天现有确诊病例数据（感染者，不包括已治愈和病亡人数，下同）和治愈者数据见图. 数据显示在2月12日现有确诊的感染者数达到最高：298人，随后快速下降。相应的累计治愈者人数则从2月12日后快速上升。累计220现有确诊的感染者数目的总体变化并不是服从指数变化规律，但分段的数据可用指数曲线（log 标度时的直线）很好的近似拟合. 这一现象可解释为：在不同阶段采取了不同的医疗措施和防控策略。

综上所述，模拟曲线和最终结果似乎显示本文提出的NSIR模型能够定性的解释四川新型冠状病毒疫情中的一些现象和医学界对疫情结束期的估计。

7基于Levenberg-Marquardt算法的模型改进

为提高模型预测的精度与运算的速度，运用另一种算法用于BP神经网络模型求解，致力于减少残差和减少迭代次数。因此，引入Levenberg-Marquardt算法用于模型求解。

上文指出了无症状感染者的存在与数量是流行病传播的重要因素，有效的阻断是消除流行榜传播的重要措施. 传播指数刻画出了无症状感染者和有症状感染者的初始比值、感染速率和感染的阻断对传染病传播的重要影响.

针对无症状感染者，首先应该最这些人员采取隔离医学观察，并在隔离开始当天和解除前一天进行两次核酸检测。目前无症状感染者的报告、流行病学调查和密切接触者管理的要求和确诊病例要基本一致。各级各类医疗卫生机构一旦发现了无症状感染者，应当在两个小时之内进行网络直报，同时在24小时之内完成流行病学调查。对发现的无症状感染者，采取14天的集中医学观察，应该在连续两次标本核百酸检测阴性才可以解除隔离，这是对无症状感染者采取的一系列管理措施。为了进一步加强对无症状感染者的监测，还要进一步加大针对性筛查力度，将监测范围进一步扩大到已经发现的病例和无症状感染者的密切接触者、聚集性疫情、重点地区和重点人群的主动筛查。同时，还将发挥社区、发热门诊的监测作用，根据病例线索，做好传染源追踪管理，通过提高监测的敏感性，及时发现无症状感染者，并及时采取集中隔离措施。对发现的无症状感染者要及时开展流行病学调查，查清他们的来源，并公开透明地发布相关信度息。

8总结

根据上述的研究表明，可以明显看到COVID-19确实是一种大流行病，虽然死亡率比不过SARS以及MERS，但它具有高传染性和无症状携带者传播性。自武汉发现首例新型冠状病毒，迄今为止，全球超过200多个国家和地区均出现了新型冠状病毒感染者。人类在病毒面前是一个命运共同体，在此时刻，一定要互帮互助、同心协力！

参考文献

[1]  卢晓燕，郭立征. 一种新型冠状病毒--萨斯（SARS）病毒[J]. 中华预防医学杂志，2003，037（004）：281-283.

[2]  杨立平. 3例聚集性发病新型冠状病毒肺炎CT表现[J]. 中国医学影像技术，2020，36（2）.

[3]  范保星，解立新，田庆，et al. Serology and Pathogenesis of SARS Virus and Its Clinical Related Research%新型冠状病毒血清学和病原学的临床相关研究[J]. 中华医院感染学杂志，2005，015（001）：1-4.

[4]  徐建国. 新发传染病的现状与对策[J]. 中华流行病学杂志，2003，24（5）：340-341.

[5]  Jin Z . 传染病动力学的数学建模与研究[M]. 科学出版社，2004.

[6]  王陇德. 我国重大传染病控制中的问题与对策[J]. 中华医学杂志，2004，084（023）：1944-1947.

[7]  中华医学会传染病与，寄生虫病学分会，肝病学分会. 病毒性肝炎防治方案：中华医学会传染病与寄生虫病学分会、肝病学分会联合修[J]. 肝脏，2000，5（4）：257-263.

[8]  Gerald T Keusch. The History of Nutrition：Malnutrition，Infection and Immunity[J]. Journal of Nutrition，2003，133（1）：336S-340S.