Burgers-Sharma-Tasso-Olver 方程的孤子分子及其半周期扭结子解

陈 立，费金喜，施苏广

（丽水学院工学院，浙江丽水323000）

0 引言

由于孤子分子在光学系统[1-4]、Bose-Einstein凝聚态[5]、非线性光学等众多领域有广泛应用，研究人员一直在持续深入地研究孤子分子，并已经建立了一系列孤子分子的理论体系[6-7]。最近呼吸孤子分子在锁模光纤激光器实验中被观察到[8]，这进一步激发了大家探究孤子分子机理的兴趣。孤子共振理论被广泛应用于各种可积系统中，通过改变孤子的共振条件，我们可以得到多种类型的共振激发模式。在此基础上运用线性叠加原理和Bell多项式构造共振解[9]，并借助Hirota的直接方法和Backlund变换的手段，Lou等研究人员在Burgers方程和Sharma-Tasso-Olver（STO）方程中发现了孤波解的裂变和聚变[10]现象。结合速度共振机制，Lou等研究人员还得到了应用于流体系统、非线性光学领域、5阶KdV方程、KdV-Sawada-Kotera方程和KdV-Kaup-Kupershmidt（KdVKK）方程中的不同类型孤子分子，弄清了这些孤子分子的形成机理和发展过程。近年来也有不少学者从数学和物理不同维度出发，对不同耦合性Burgers系统和STO方程进行了广泛的研究，但是到目前为止，相关学者对（2+1）维BSTO方程的研究甚少。在本文中我们主要建立并求解了非耦合的（2+1）维BSTO方程的新型孤子分子，并找到半周期扭结子解。

1 （2+1）维BSTO方程和它的多孤子解

从（1+1）维 Burgers族方程[11-13]出发：

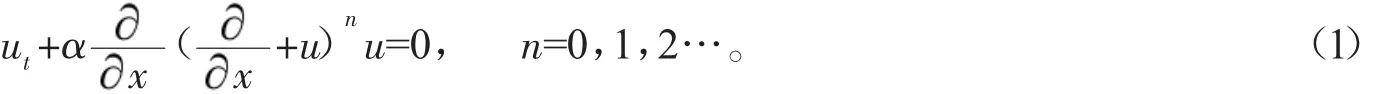
在文献［14］中，我们将（1）式推广到（2+1）维的形式：

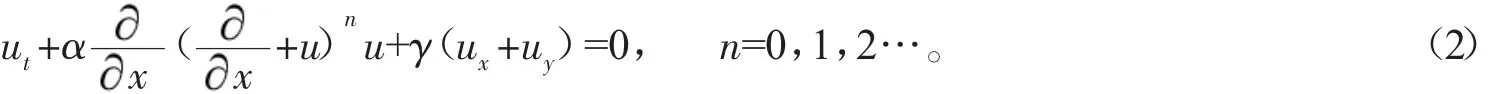
取 n=2 时，（2）式可转化为

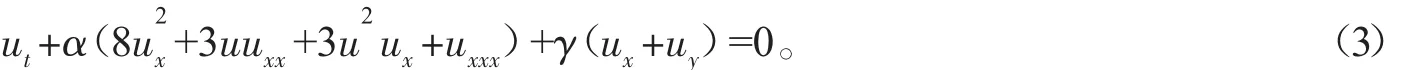
而（3）式的拓展形式即为BSTO方程：

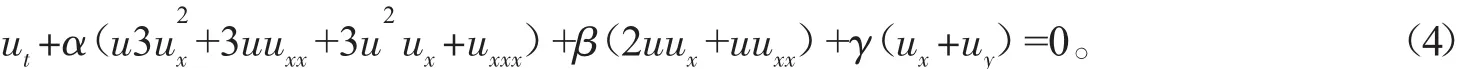
当系数 α，β，γ 取不同值时可以将（4）式转化成不同类型的方程。如当 α=0，γ=0 时，（4）式转化为（1+1）维Burgers方程；当 β=0，γ=0 时，（4）式转化为 STO方程；当 β=0 时，（4）式转化为（2+1）维 STO方程，如（3）式所示。

我们根据Backlund变换，得到方程(4)的解为

将（5）式代入（4）式得到

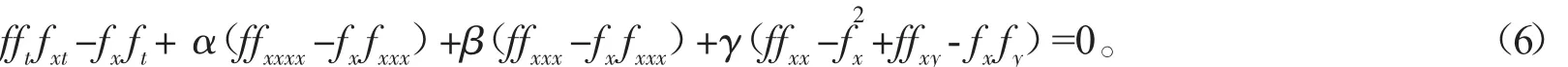
假定（6）式中奇性流形f满足

式中 ai为任意常数，ki、pi为波数，wi为频率，ηi为初相，波数、频率满足色散关系

将（8）式代入（7）式就得到BSTO方程的多孤子解

在这一章节中我们利用BSTO方程的多孤子解——式（9），求其在不同参数条件下的半周期扭结子解，并揭示它们的裂变和聚变现象。取N=2，并假定

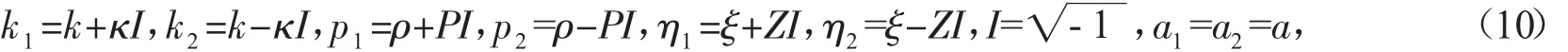
将（8）式和（10）式代入（7）式有

式中 Ω=ακ（κ2-3k2）-2βkκ-γ（κ-P），ω=αk（k2-3κ2）-β（k2-κ2）-γ（k+ρ），a、k、κ、ρ、P、ζ、Z 为任意常数。将（11）式代入（5）式得到BSTO方程的解为：

明显地，解（12）式存在奇点。为了消除奇点，我们利用共振条件，得到了BSTO方程的半周期解的简单形式

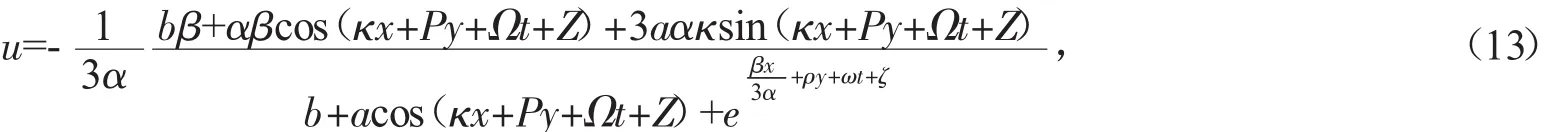
式中

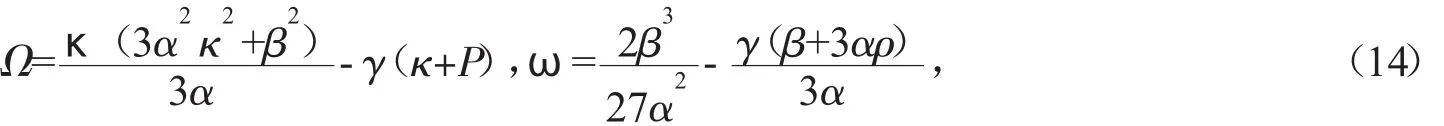
b为任意常数。

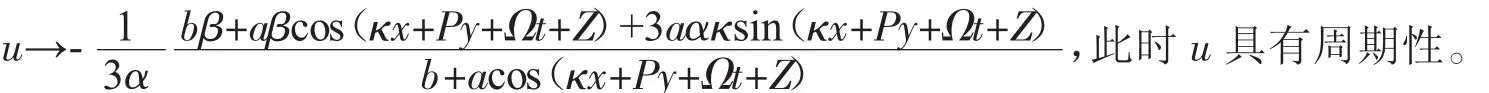
2 半周期扭结子解以及它们的裂变和聚变

图 1 （a）（b）（c）分别表示 t=-4，0，4 时的波形。

选取（9）式中合适的参数，可以得到孤子的裂变和聚变结果。如取N=4，则（9）式可转化为

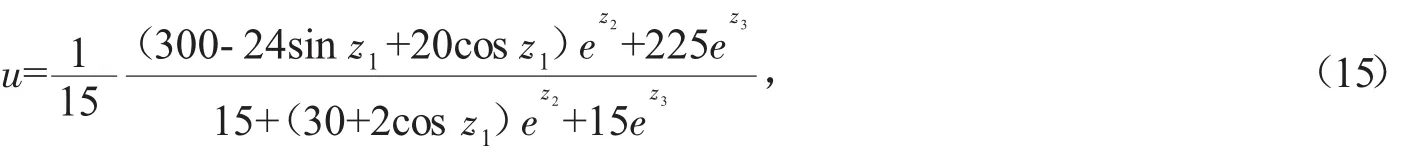
图2 （a）当t=0时，孤子裂变图；（b）当y=0时，孤子裂变图

图3 （a）当t=0时，孤子裂变图;（b）当y=0时，孤子裂变图

图4 （a）当t=0时，孤子聚变图;（b）当y=0时，孤子聚变图

图5是（18）式的孤子聚变三维图。比较图5（b）与图4（b）我们发现图5（b）清楚地显示了两个半周期扭结子聚变成通常的扭结子的现象。

图5 （a）t=0时孤子聚变图;（b）y=0时，孤子聚变图

3 BSTO方程的孤子分子

在这一章节中，我们利用速度共振条件，研究BSTO方程的孤子分子的特性。首先我们给出BSTO方程的波数、频率共振条件为

其次将（8）式代入（19）式得到波数 ki，kj关系式为

最后在 BSTO 方程的孤子分子式（9）中，取 N=2，且当 a1=a2=1，α=γ=1，β=-1，p1=2，p2=1，η1=0，η2=5时，再结合（8）式和（20）式，（9）式可转化为

通过模拟计算得到（21）式在势场ux中不同时刻的孤子分子图（如图6），演化过程表明两孤子所形成的孤子分子在传播过程中它们的相对位置在不同时刻始终保持不变。其内在原因在于两孤子的传播速度满足速度共振机制，即两孤子的传播速度相同。

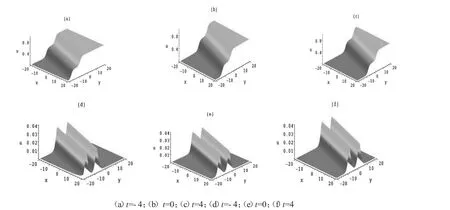
图6 当N=2时，（21）式在势场ux中不同时刻的孤子分子图

若我们选取 N=4，a1=a2=1，α=γ=1，β=-1，p1=2，p2=1，p3=-2，p4=-1，η1=0，η2=5，η3=0，η4=5，再结合（8）和（20）式，则（9）式可转化为

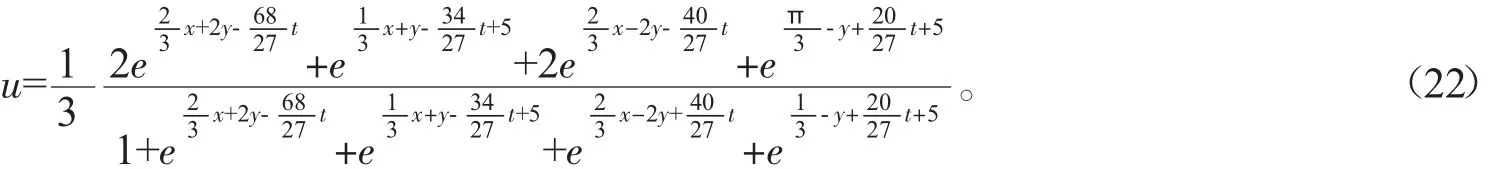
通过模拟计算得到（22）式在势场ux中不同时刻的四孤子分子图（如图7），演化过程表明四孤子也有在传播过程中它们之间的相对位置在不同的时刻始终保持不变的特性，这类同于N=2时的传播情形。

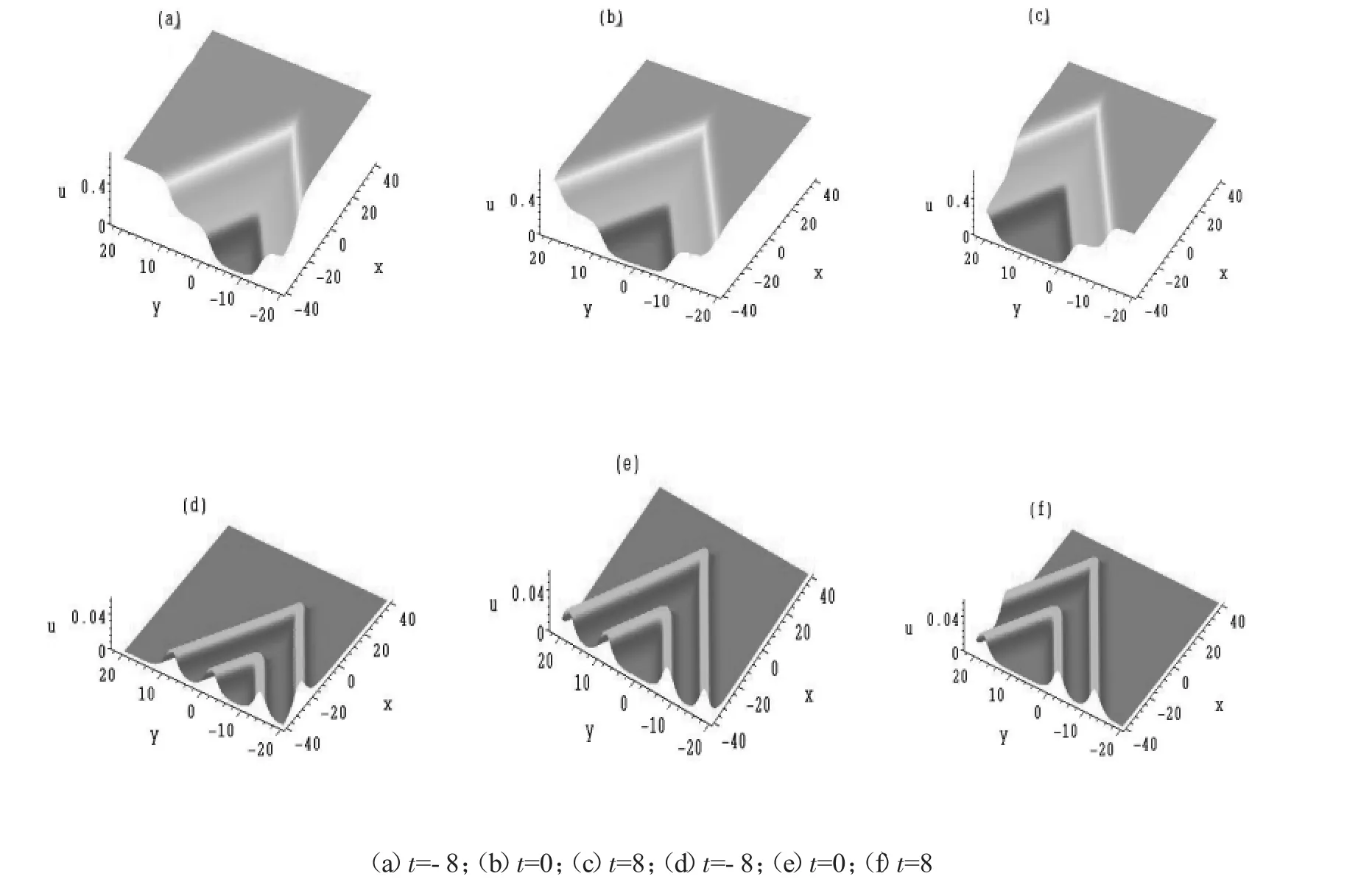
图7 当N=4时，（22）式在势场ux中不同时刻的孤子分子图

4 结语

本文利用速度共振机制，得到了（2+1）维BSTO方程的解即二孤子分子和四孤子分子，并分析了其特性。接着讨论了常规扭结子和半周期性扭结子之间的相互作用，即聚变和裂变现象。文中对孤子分子和扭结子的剖析为开展应用物理实验和理论研究提供了一个新的思路，具有一定的科学指导意义。