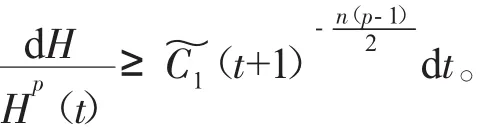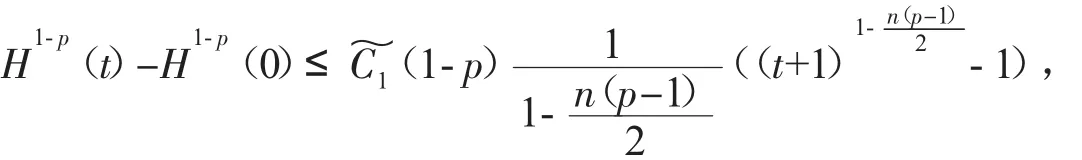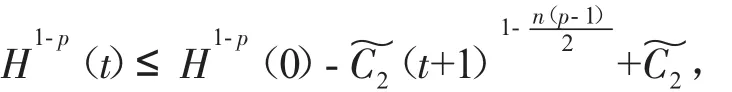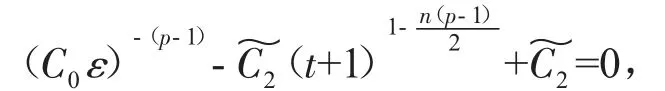半线性热传导方程Cauchy问题生命跨度估计
林银河,徐根海,杨姗姗
(1.丽水学院工学院,浙江丽水323000;2.浙江理工大学理学院,浙江杭州310018)
0 引言
根据定义,生命跨度T(ε)是指解的最大存在时间。当T(ε)=+∞时,表明解整体存在。Li和Chen[1]建立了如下形式的生命跨度下界估计:

其中C是一个与n,p有关的正常数,但与ε无关,不同的地方取值不一样。
现在研究以下n维半线性热传导方程的Cauehy问题:
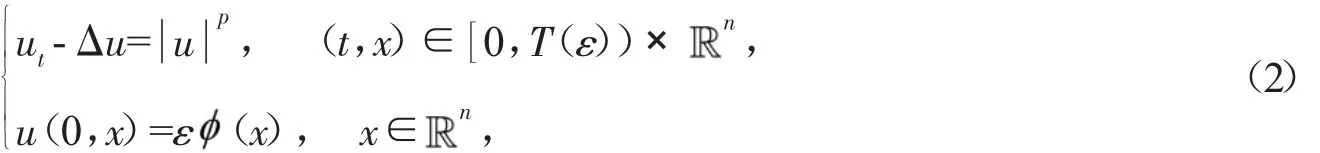
和

其中ε表示描述初值小性的参数。上述两个问题的方程都是反映扩散的方程,通常用于种群动力学和几何学中。这两个问题的主要区别在于非线性项,问题(2)中的非线性具有非负性,这有利于得出下界估计,而问题(3)的非线性不具有非负性。与上述两问题相关的更一般的非线性热传导方程模型为

其中u(t,x)表示化学反应中的温度,(f正)表示热源,可参考Hu[2]关于模型(2)的详细介绍。对Cauchy问题(2)的研究源于Fujita[3]于1966年的开创性工作。他证明了问题(2)存在临界指标p=pF(n)=(Fujita临界指标):即当时,对于任何非负且非平凡的初值,解将在有限的时间内破裂:而当p时,则存在小初值整体解。随后,文[4-7]研究了临界指标情况,并证明了该情形解也将在有限时间内破裂。另外,Hu在文[2]的第5章中用反证法证明了当1 有一个有趣的现象是以下小初值半线性耗散波动方程的柯西问题: 与(2)具有相同的临界指标,参见[8-14]及其中的参考文献。 引理1 热核E(t,x)的傅里叶变换为 证明 由傅里叶变换的定义可知 于是(8)得证。基于此,可以证明 E(t,x)的半群性质,即: 其中★表示卷积。 证明 由(8)式可知E(t,x)的傅里叶变换为 由此可得 对上式再作傅里叶逆变换便可得(10)式。 首先考虑定理1的证明。根据Diuhamel原理,问题(2)的解可以表示为 在这里我们使用了E(t,x)的半群性质。 令 和 则由 Ho¨lder不等式,可得 令 则有 代入(17)式,得 其中C0表示一个与ε无关的正常数。 注意到当 0≤τ≤t时,有 2(t+1)≥2t+1-τ≥t+1,则由 Ho¨lder不等式可以估计非线性项 N(t): 其中C1表示一个与ε无关的正常数。 结合(13)(19)(20)和(21),可得 令 则有 和 由此可得H(t),亦即F(t)的生命跨度上界估计: 积分上式,可得 即 整理后,可得 其中 进一步,可得 于是当 即当 时,有 从而 这样就证明了生命跨度上界估计为 从而完成了定理1的证明。 以下考虑定理2的证明。事实上,只需要证明解的非负性,则问题(3)就能转化为问题(2),从而就可以用上面的方法得到同样的生命跨度上界估计。下面证明问题(3)的解是非负的。首先考虑如下Cauchy问题: 由热传导方程基本解的正性(见(13))和初值的假设,可知 再由热传导方程解的唯一性,可知 这样就证明了Cauchy问题(3)解的非负性,从而问题(3)中的非线性项,故只需重复定理1的证明步骤即可证明定理2。

1 热核的半群性质






2 主要结论的证明