江苏省通南地区河网水量水质数值模拟研究
方浩川,许仁义,钱睿智,汪凌翔
(1.扬州大学 水利科学与工程学院,江苏 扬州 225009; 2.江苏水文水资源勘测局扬州分局,江苏 扬州 225000)
1 概 述
江苏省扬州市通南地区位于长江下游沿江地区,地势平缓,属于亚热带季风气候,四季分明,雨水充沛,年平均降水量为1 031 mm,但水文条件十分复杂,地表径流在空间和时间上分配很不均衡,具体表现为南部径流多于北部,丰水期降水值在年降水量中占了很大比重,而且由于许多河流河床都比较窄,城区实际往外(长江及周边河流)排水口较少,水流常常被堵在城区,排水效果不是很完善,导致在汛期常常可能发生洪涝灾害。在水质问题上,由于近些年扬州城市发展较为迅速,且在水污染整治问题上有所欠缺,导致水污染问题日益严重[1]。本文基于一维非恒定水流流动基本方程组及一维污染物对流-扩散方程,建立了扬州通南地区城市河网一维水量水质模型[2],模型采用隐格式[3]进行数值求解,从而模拟出水流过程及污染物输运扩散过程,为以后改善该地区的水质以及水生态打下了基础。
2 水量水质模型
2.1 水量模型
水流在平底、棱柱形明渠中一维非恒定流动的基本方程组—圣维南方程组[2]:
(1)
(2)
式中:A为过水面积,m2;Q为断面流量,m3/s;Z为水位,m;α为动量修正系数;K为流量模数;qL为旁侧入流,m2/s,入流为正,出流为负;vx为入流沿水流方向的速度,m/s。
2.2 水质模型
河网对流污染物输移问题的基本方程[4]为
(3)
式中:Ex为纵向分散系数;C为水流输送的物质浓度;Sc为与输送物质浓度有关的衰减项,Sc=KdAC,Kd为衰减因子;S为外部的源或汇项。
3 模型建立与验证
3.1 河网概化
本实验是对江苏扬州邵伯湖供水区通南地区所属河流进行河网水动力及水质数值模拟,其具体包括邵仙引河、老通扬运河、小涵河、顾圩河、白塔河、灰粪港、向阳河、红旗河八大主要河流,以及邵仙闸洞、宜陵地涵、通江闸、河口闸四大主要水利工程建筑物。根据通南地区各河流河床断面数据及过水情况分析,为符合工程计算要求,概化出扬州市通南地区河网平面图见图1。

图1 扬州通南地区河网概化图
3.2 断面概化
数模过程根据实测断面资料,选用等腰梯形断面布置。
3.3 边界条件
根据2016年5月30—31日扬州市通南地区各个测量点实测资料,以及流域内各水工建筑物工作情况,得出该段时间内除通江闸为关闭外,其余闸门都正常过流。水流从邵仙闸洞入流,途径老通扬运河,连小涵河与顾圩河,经宜陵地涵与白塔河相通,最后经小涵河、顾圩河及河口闸向外排出。结合河网边界条件给定条件,设定邵仙引河上游为流量进口边界,顾圩河、小涵河、河口闸给定水位出口边界。
3.4 时间、空间步长
由于天然河道河床高程沿着纵向不断变化,所以在构建数值模型时在空间步长的选择上需要贴合真实地形的需求。理论上而言,模型计算的时间、空间步长越小,计算结果的误差就会越小,但相对的产生的计算量就会变大,若时间和空间步长过大,容易产生过大的数值坦化,无法精确反映真实情况,因此权衡效率及误差是步长选择的根本。因此根据河网各河道断面实测数据,采用空间步长为800~1 500 m,时间步长则为200 s。
3.5 初始条件
模型的初始条件包括流量、水位及水质情况,设定初始条件的意义就是为了能更贴近真实河流水流情况,使模型开始计算时水流流速、水位及污染物浓度情况能与实际情况一致,使计算结果精确度更高,本次模拟水流上下游边界条件均采用31日10 h实测数据,内部水流情况为给定流速为零,水位统一为3.6 m,各污染物浓度给定其一个均值情况,并以在该边界条件下模型正常运行4 d之后,待其流速、水位情况基本达到稳定之后各河段水动力及水质情况为后续模型计算的初始条件[5]。
3.6 模型率定及验证
3.6.1 参数率定
本次模型选用2016年5月30—31日通南地区水文站实测资料进行模型参数率定,通过反复调整河床糙率数值以达到水位及流量计算值能与实测值尽量吻合,并根据查阅扬州市水质情况资料,在模型中加入点污染源,使得监测点的模型水质计算值更加贴合实测值。通过调整,得到各河流参数结果见表1。

表1 参数率定结果
3.6.2 计算结果
并根据2016年10月24—25日的实测值进行模型验证,验证结果如下:表2~3为河网内部各测量点水位及流量验证对比结果;表4~7为河网内部各测量点TN、TP、NH3-N及CODMn质量浓度验证对比结果。
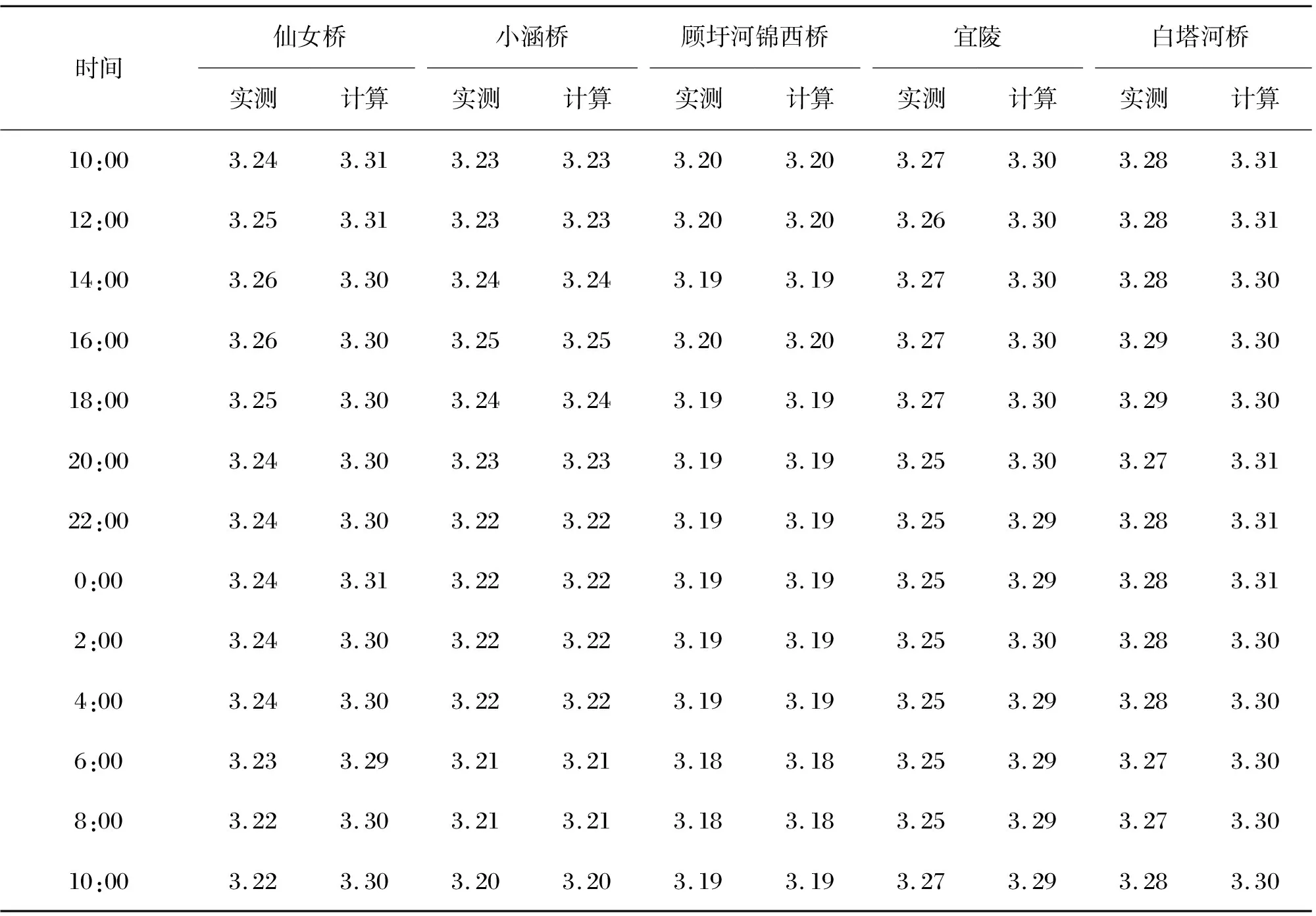
表2 模型水位模拟与实测对比 单位:m

表3 模型流量模拟与实测对比 单位:m3/s

表4 模型TN质量浓度模拟与实测对比 单位:mg/L

表5 模型TP质量浓度模拟与实测对比 单位:mg/L

表6 模型NH3-N质量浓度模拟与实测对比 单位:mg/L
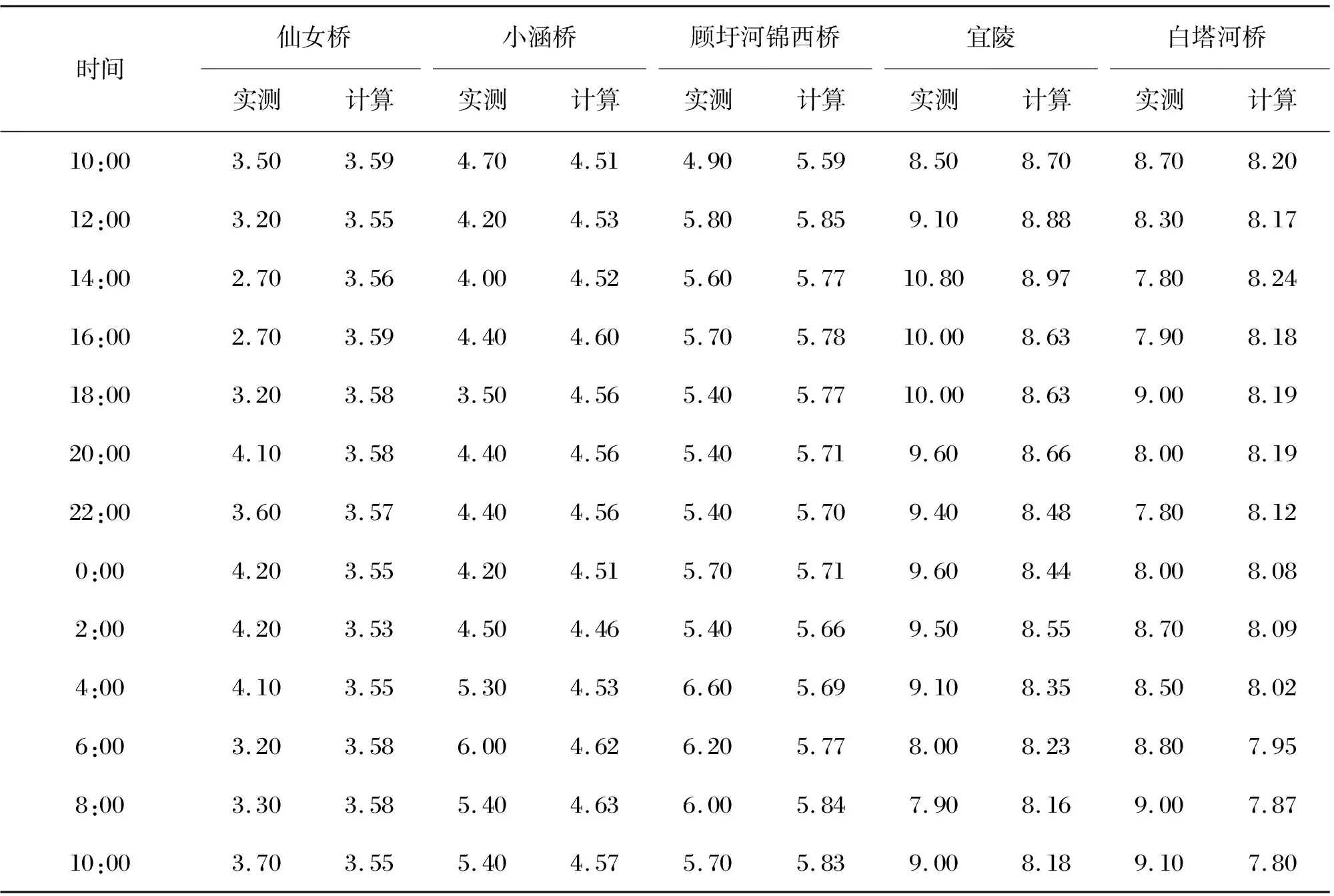
表7 模型CODMn质量浓度模拟与实测对比 单位:mg/L
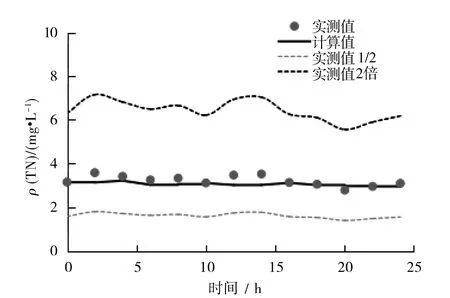
图3 宜陵处TN质量浓度计算与实测对比
通过观察表2~7或图 2~3可以发现,水位与流量的实测值与计算值曲线都较为接近,具体有所偏差原因可能是由于地下水及周边细小支流影响,但计算结果还是保证了在误差允许的范围内。在污染物浓度表现上,由于扬州水系支流十分发达,大部分工厂,房屋都是建在河流旁边,所以每天不同时刻都会有不定量的工业污水、生活污水排入河中,而这一部分的排入点污染浓度是无法精确到每一个时刻的,只能取一个近似的平均值,所以在计算结果上,相较于实测值的某时刻的突然变化,污染物浓度曲线所表现的就比较平缓,但也保证了计算值并没有超过实测值的2倍和1/2间的范围,且变化趋势也较为统一。模型率定结果表明,模型参数选取合理,所建立的模型能够模拟东区河道内的水流运动情况及水质变化,为改善东区水动力条件及水环境改善提供了技术支撑。

图2 宜陵处流量、水位计算与实测对比
4 结 论
本文通过对扬州市通南地区河网水动力及水环境经行数值模拟,建立了通南地区水动力-水环境河网数学模型,通过实测水文资料对模型进行了率定,并经水文站实测值与计算值验证对比情况可知,本模型无论在水位、流量及水质计算上都与实测值贴合程度都较好,计算结果有较好的精确度。因此,该模型能够用于分析在不同水资源调度情况下扬州内部河网水动力条件的情况和水质情况。且根据实测数据分析,邵伯湖供水去扬州通南地区河网水流从邵仙河引入后,绝大部分都从小涵河及顾圩河流出,其河网中部及南部地区水流流速都较慢,而且由于河流断面都较为狭窄,所以在该闸门控制现状下,如遇到大规模降雨会有洪涝灾害的可能。
——以莲花县为例

