考虑代理人两类过度自信行为的委托代理关系模型

陈克贵，任 亮，王新宇

(1.中国矿业大学经济管理学院，江苏 徐州，221116；2.武汉科技大学恒大管理学院，湖北 武汉，430065)

委托代理理论一直是经济管理研究的重点课题[1-2]。现实经济活动中，人的行为受情感和心理等多要素的影响，因而会表现出非理性行为，此时传统委托代理理论的“理性人”假设与实际情况并不相符。已有的行为学和心理学研究表明，不同决策者在各自的决策中存在不同观点，之所以出现这种情况，源于决策者在决策过程中表现出的过度自信行为[3-4]。作为一类非理性行为，过度自信引起了行为运作管理、行为经济和行为金融领域众多研究者的关注。Russo等[5]发现多数管理者都过高估计了企业的盈利能力和自身的经营能力。例如，柯达公司(Eastman Kodak Company)由于对自身技术水平的过度自信，忽略了对未来的规划，导致销售业绩下滑并最终衰败；前诺基亚首席执行官 Stephen Elop 坚持使用塞班系统，并且高估自己手机品牌的竞争力，他的过度自信行为是导致手机销量大幅下滑的重要原因，最终诺基亚被微软收购。

国内外研究者对过度自信行为下的委托代理关系进行了大量的理论和实践探讨，取得了一些成果。Moore等[6]回顾了与过度自信相关的研究文献并总结出三类过度自信行为：第一类是过高估计，主要是指过度自信者过高估计自身的能力、绩效和成功机会等；第二类是过高定位，指过度自信者相对于他人能力高估了自身能力；第三类是过度精确，指过度自信者相对于实际水准高估了自己的预测准确性。Fischhoff等[7]和Weinstein[8]分别证实了过度精确和过高估计两种过度自信行为的存在。Ren等[9]采用实验方法来研究报童模型中的过度自信行为(特别是过度精确)，证明其是导致报童模型实验中决策偏差的一个重要原因。Lu等[10]针对由理性的零售商和过度自信的供应商组成的供应链，探讨了不同库存管理模式下的决策问题，并分析了供应商的过高估计和过度精确两类过度自信行为对供应链的影响。周永务等[11]假设过度自信的零售商低估了随机市场的波动性却高估了商品需求的期望均值，并结合报童模型从供应链协调视角分析供应链契约机制和零售商的过度自信行为，结果表明过度自信会导致供应商决策偏差及零售商利润损失。方舟等[12]以低估自身的信息劣势作为做市商过度自信的表现(过度精确)，探讨其如何影响不对称信息下的金融市场。Keiber[13]，de la Rosa[14]、黄健柏等[15]和Chen等[16]分析了委托代理框架下过度自信行为对激励合同的影响。Ludwig等[17]研究表明，一定程度的过度自信倾向是有益的，可促使代理人提高努力水平，进而提高成功可能性。Sandroni等[18]探究了保险市场中代理人对风险水平的认知有过度自信倾向时的合同设计问题，进而分析了代理人过度自信行为和最优激励机制的关系。陈其安等[19]建立了过度自信行为下股份公司中的委托代理关系模型，分析了过度自信行为对委托代理关系的影响机理。庄新田等[20]在探讨动态激励契约设计问题时同时考虑了过度自信因素和监督机制。李娟等[21]针对委托人和代理人双方不同的过度自信组合问题，分析比较了过度自信行为下的线性激励合同和阈值合同。

本文在已有研究的基础上并结合传统委托代理理论，针对过度自信的代理人对自身努力效果以及产出方差两方面的预测偏差，探讨了委托人面对过度自信代理人的激励合同设计问题。不同于文献[11，16，22]仅用单参数描述过度自信行为，也不同于文献[23-25]仅单独考虑过高估计或过度精确等行为，本文同时采用不同的参数考虑代理人的过高估计和过度精确两类过度自信行为，分析其如何影响委托代理关系及参与双方的策略和收益，并通过数值算例对研究结论进行验证。

1 问题描述与模型假设

本文研究的问题是：在代理人过高估计和过度精确两类过度自信行为下，委托人如何设计有效的激励合同以激励代理人努力工作，进而最大化委托人效用。为了便于论述及必要的数学简化，作如下假设：

假设1理性的委托人雇佣过度自信的代理人，产出函数为：π=a+θ，其中a为代理人的努力水平，θ为随机因素并且服从正态分布，其均值为0、方差为σ2 [1-2]。完全理性的委托人能正确理解θ的概率分布，而过度自信的代理人不能对其正确认识，代理人对产出函数的均值及方差的估计量都有一定程度的偏差，即过度自信的代理人眼中的随机产出函数为[10]：

π0=μ(λ)a+ω(η)θ

(1)

式中：μ(λ)≥1，μ′(λ)≥0，μ(0)=1，且0<ω(η)≤1，ω′(η)≤0，ω(0)=1。ω(η)θ服从正态分布，其均值为0、方差为ω2(η)σ2，并且ω2(η)σ2≤σ2成立。λ>0和η>0分别表示代理人的过高估计和过度精确程度，当λ和η增大时，过度自信的代理人的主观期望产出会逐渐高于实际情形，而其眼中的产出方差则要越来越小于实际的产出方差，也就是说，λ和η同代理人的过度自信程度成正比关系，λ=η=0时，代理人完全理性。

假设2委托人可观测到产出π，但观测不到代理人的努力水平a，过度自信的代理人的报酬取决于产出，采用线性激励模式：s(π0)=α+βπ0，记为(α,β)，这里α表示固定收益，β为代理人从产出中得到的报酬。假设代理人的努力成本C(a)=ba2/2，b>0为努力成本系数[1-2]。

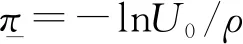
(IR) CE=α+βμ(λ)a-

(2)

假设4以上假设为委托人和代理人双方的共同知识。为方便起见，将努力成本系数b、风险规避程度ρ与产出方差σ2之积(A=bρσ2)称为传统因子。

2 代理人过度自信情形下的模型构建

根据模型假设，针对有过度自信倾向的代理人，风险中性的委托人的期望收益为：

E(πP)=a-α-βμ(λ)a

(3)

代理人相应的目标为实现其自身期望效用的最大化：

E[-exp(-ρ[α+β(μ(λ)a+ω(η)θ)-ba2/2])]

(4)

最大化代理人期望效用的问题可转化为最大化其确定性等值[1-2]：

CE=α+βμ(λ)a-ba2/2-ρσ2β2ω2(η)/2

(5)

委托人的激励合同设计问题是在代理人有过度自信倾向时，通过确定针对代理人的最优激励合同(α,β)来最大化其期望收益。委托人制定的激励合同必须满足两个条件：其一，该合同下代理人的期望效用不小于其保留效用，即满足IR约束(式(7))；其二，代理人选择的最优努力程度可最大化其期望效用，即满足式(8)的激励相容约束(incentive compatibility constraint, IC)。因此委托人的最优化激励问题可归结为：

(6)

s.t. (IR) CE=α+βμ(λ)a-

(7)

(8)

式中：上角标*表示各变量取得最优值情形。

由式(8)的一阶最优条件，可以得到过度自信代理人的最优努力程度为：

a*=μ(λ)β/b

(9)

通过求解模型式(6)～式(8)，可得到代理人过度自信情形下，委托人和代理人的最优决策和收益如以下定理所述。

定理1在代理人过高估计和过度精确的过度自信程度分别为λ和η的情况下，委托人制定的激励合同(α*,β*)以及代理人的最优努力程度a*的最优配置如下：

(10)

(11)

(12)

委托人的最优期望收益为：

(13)

证明：将代理人最优努力程度的一阶等价条件a*=μ(λ)β/b代入式(7)的IR约束，最大化问题是IR条件为等式，即

将上式以及IC一阶等价条件a*=μ(λ)β/b代到委托人的目标函数式(6)，消去α和a，则委托人的目标是制定激励系数β来最大化其期望收益E(πP)：

当代理人完全理性即λ=η=0时，可得到

相应的代理人的努力程度为

委托人的期望收益为

其中，下标HM代表Holmstrom & Milgrom模型[1-2](代理人完全理性时的模型)。也就是说，此情形的最优解与传统的委托代理理论和HM模型的结论完全一致，HM模型仅是本文模型的一种特殊情况。

3 模型分析与结论

本节在代理人有过度自信行为的前提下探讨以下问题：①最优激励合同呈现出的特征；②两类过度自信行为对委托、代理双方的决策和最终收益的影响；③委托人不考虑代理人的过度自信行为的后果。

结论1在均衡条件下，当两类过度自信程度λ和η逐渐增大时，代理人相应的最优努力程度a*也逐渐增加，并且最优努力程度a*随着因子A的增大而减少；当过度精确程度η逐渐增大时，最优激励系数β*也逐渐增加，并且β*随着因子A的增大而减少；当因子A足够大时，β*随过高估计程度λ的增大而增大；反之，当因子A较小时，β*随过高估计程度λ的增大而减少。

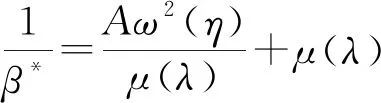
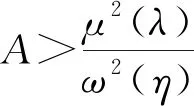
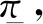
由结论1和结论2可知，代理人的最优努力程度a*和委托人的最优期望收益E*(πP)都随着传统因子A的增大而减少，表明最优努力程度a*和委托人的最优期望收益E*(πP)都随着努力成本系数b、风险厌恶程度ρ、产出方差σ2的增加而降低，与道德风险情况下HM模型[1-2]的结论是一致的。

通过结论1和结论2，还可得到如下的推论。

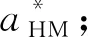
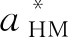
由式(11)可知，

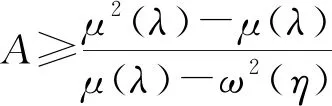
结论3当委托人忽视代理人的过度自信行为时，其实际的期望收益将减少。

证明：当委托人不考虑代理人的过度自信行为时，其实际的期望收益为：

考虑代理人的过度自信行为时，委托人的实际期望收益为：

E[πP(α*,β*)]=a-α*-β*μ(λ)a。

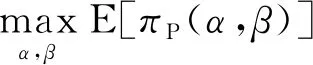
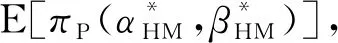
结论3表明，委托人在制定激励合同时，不可忽视代理人的过高估计和过度精确这两类过度自信行为因素的影响。

下面分析代理人的两类过度自信程度如何影响其实际期望效用。

代理人过度自信时的信念期望效用是指过度自信代理人根据其对将要实现的信念产出π0的判断做出努力程度a*的决策所确定的期望效用值CE(α*,β*)；而过度自信代理人的实际期望效用是指根据实际的产出π以及各自的决策所确定的期望效用[26-27]。

结论4代理人过度自信时的实际期望效用要低于代理人完全理性时的实际期望效用，并且两者之间的偏差Δ会随着代理人的两类过度自信程度λ和η的增大而逐步增大。

证明：代理人有过度自信倾向时的信念期望效用为：

CE(α*,β*)=

α*+β*μ(λ)a*-ba*2/2-ρσ2β*2ω2(η)/2，

过度自信代理人的实际期望效用为：

CE(actual)=α*+β*a*-ba*2/2-ρσ2β*2/2，

二者之差为

Δ=CE(α*,β*)-CE(actual)=

即CE(actual)≤CE(α*,β*)成立。

结合式(9)可知：

结论4表明，A足够大时，两类过度自信行为将导致代理人实际期望效用的损失，并且随着代理人两类过度自信程度λ和η的增加，期望效用的损失量也会加大。

由结论1、结论2和结论4可知，当A足够大时，代理人的过高估计和过度精确两类过度自信行为对委托人和代理人双方的决策和收益的影响是一致的，也说明这两类过度自信行为对双方的决策和收益的影响是相互替代的关系。

4 数值分析

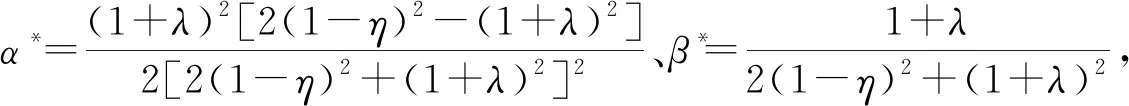
在其他参数不变的情况下，当代理人的过高估计程度λ和过度精确程度η均在[0,1]内变动时，分析a*、β*和E*(πP)等变量的变化趋势，如图 1 ～图 3所示。为了对比分析，文中还给出参数b=1、ρ=1、σ2=1，即A=bρσ2=1时，β*随λ和η的变化趋势，如图4所示。

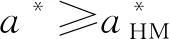
图1 代理人过度自信程度λ和η对其最优努力程度a*的影响

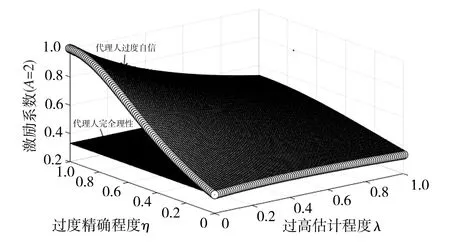
图2 代理人过度自信程度λ和η对最优激励系数β*的影响(A=2)

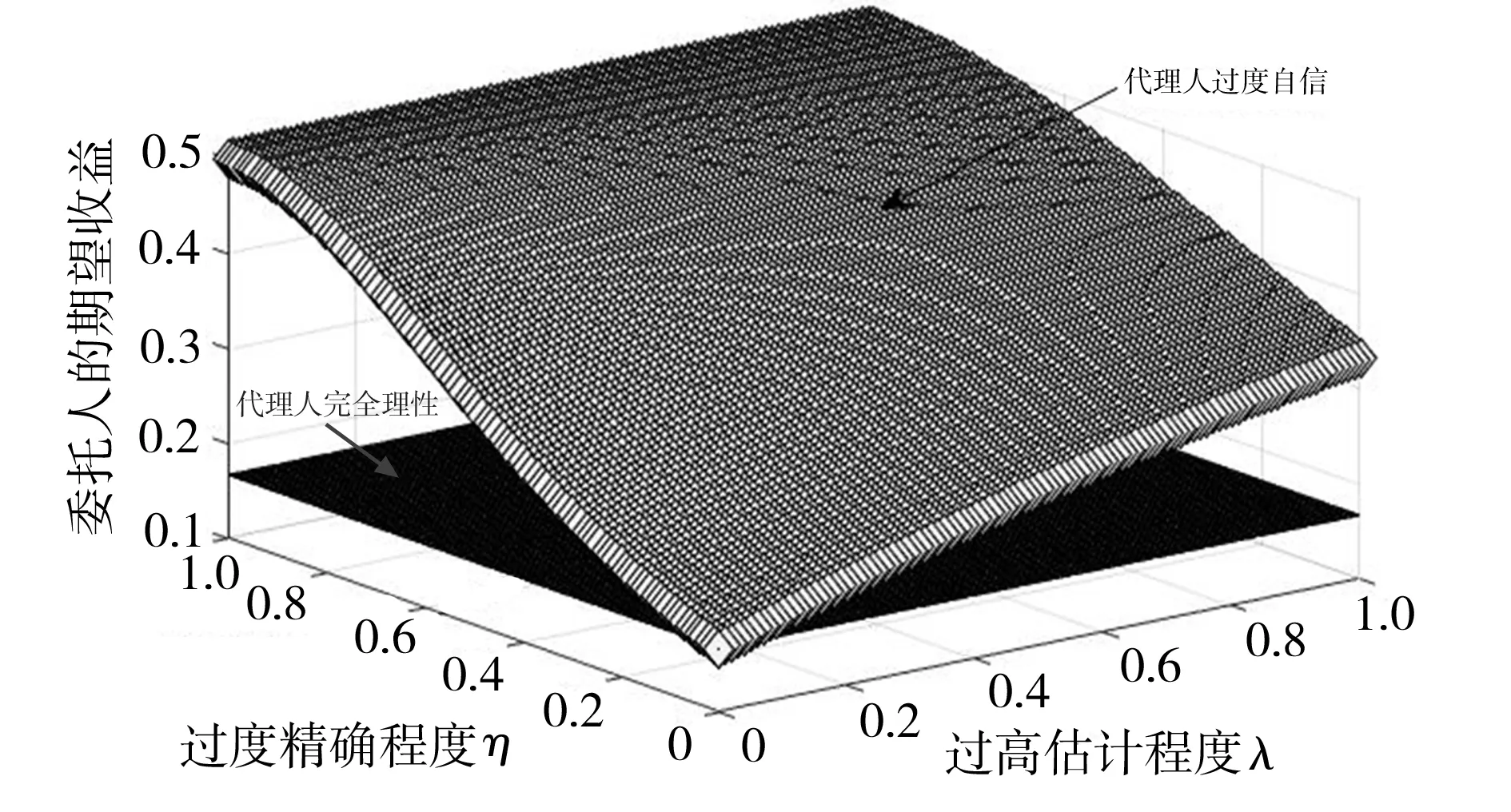
图3 代理人过度自信程度λ和η对委托人最优期望收益E*(π P)的影响

图4 代理人过度自信程度λ和η对最优激励系数β*的影响(A=1)

5 结语

本文基于代理人过度自信行为建立委托代理关系模型，同时用双参数考虑了代理人两方面的过度自信行为：过度精确和过高估计，并从理论上分析了代理人的两类过度自信行为对委托代理关系的影响。研究表明，随着代理人过度自信程度的增加，委托人相应的期望收益和代理人的努力程度都将增大，而代理人的实际期望效用却要低于理性代理人所获得的期望效用，并且当两类过度自信程度增大时，两者间的偏差也会加大，即实际期望效用越来越偏离代理人理性时的期望效用；当委托人忽视代理人的过度自信行为时，其实际的期望收益将减少；在一定程度的过度自信下，两类过度自信行为对代理人和委托人双方的影响是一致的。数值分析也验证了上述结论。

本文研究还存在着局限性：①仅考虑了代理人过度自信下的线性合同，没有同时考虑代理人和委托人双方的过度自信行为以及其他类型的激励合同(如对代理人设定目标产出的阈值合同)对参与双方的决策和收益的影响；②将代理人的两类过度自信行为假设为双方的共有信息，而在实际中，代理人可能会隐藏其真实的过度自信信息，即代理人的过度自信程度属于其私有信息；③仅考虑了单代理人模型。

下一步的研究方向为：针对代理人的两类过度自信行为是非对称信息时的最优激励合同设计问题，并同时考虑参与双方的其他非理性行为，还可考虑多代理人时的机制设计以及过度自信的代理人对自己相对于其他代理人能力的过高定位行为。