基于叶尖定时的失谐叶片-轮盘振动参数辨识仿真
(辽宁工业大学 机械工程与自动化学院,辽宁 锦州 121001)
叶片在长时间工作时容易产生裂纹、折断等现象,这大大降低了叶片的工作寿命,产生此现象的主要原因是叶片振动,因此,对叶片进行振动分析至关重要,而叶片在旋转工作的过程中,存在升速与降速的情况,不考虑转速的影响对叶片轮盘系统进行建模仿真,会导致测量结果不准确,而目前大多数的分析方法都是在不考虑转速影响的情况下进行,因此本文在考虑转速影响的情况下,对叶盘系统进行建模仿真与振动参数测量,使得出的结果更加符合实际。
本文采用叶尖定时法[1-4]的测量原理对叶片振动进行仿真分析,原因在于该方法应用广泛,与频率调制法[5]、激光全息法[6]、激光多普勒法[7-9]和声发射多普勒法[10]等其他测量方法相比,其容易安装,不会对叶片的原有材料属性造成影响,而且能够测量出较多叶片的振动参数。然而,叶尖定时法不能直接测量出叶片的全部振动参数,因此,为了解决这一问题,需结合双参数法[11]、自回归法、均布法[12]、速矢端迹法[13]等参数辨识算法辨识出叶片的全部振动参数。然而,以上所述的各种算法均不是很成熟,都存在各自的缺点,国内外很多研究者对其缺点研究与改进,提出了更加完善的参数辨识算法。如欧阳涛[14]提出了一种多传感器参数辨识算法,该方法应用多支叶尖定时传感器,并任意分布在叶轮一周。其原理是通过检测叶片顶端经过叶尖定时传感器的时间,计算其时间差值,利用叶片半径、叶片转动角速度等参数计算叶片振动位移。这种方法的适用范围广,其优点在于对传感器的安装角度、布局方式没有固定要求。因此本文利用该种参数辨识算法对恒速下叶片同步振动进行参数辨识,证明在考虑转速时对叶盘系统进行振动分析的仿真结果正确。因此,本文对考虑转速影响时的叶片轮盘振动系统进行振动仿真测量,为叶片振动测量提出了一种更加贴合实际的振动参数测量方式。
1 建立叶尖定时测振系统
本文所采用的整个叶片轮盘系统具有8 个叶片,并将整个轮盘系统看成是刚体。由此建立8 叶片振动系统模型,如图1 所示。
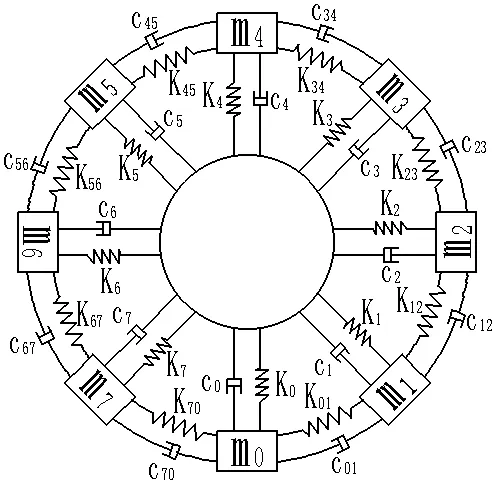
图1 8 叶片振动系统模型
由该8 叶片振动系统模型,可以得到如下公式。
整体阻尼矩阵:

整体质量矩阵:

整体刚度矩阵:
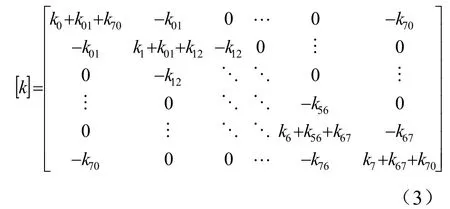
通过振动理论可列出该叶片轮盘系统的振动微分方程,其方程如下式(4)所示:

式中:{y}为振动位移,{F(t)}为外部激振力,将式(1)、式(2)和式(3)代入式(4),化简得到下式(5)。因该叶盘系统为8 叶片结构,所以i的取值为0,1……7,且令0-1=7,7+1=0。

式(5)为单叶片与单轮盘振动系统方程,由此建立单叶片振动系统模型与单轮盘振动系统模型。如图2、图3 所示。

图2 单叶片振动系统模型
为了方便测量,将激光转速传感器J0 安装在旋转轴一侧,在旋转轴上设置检测标记,使激光转速传感器能够准确捕捉到转速信号,并将此作为基准传感器,即安装角度设置为0 度,另外采用电涡流传感器采集叶片顶端到达传感器的时间信号,为了确保测量精度,将数量设置成 4 支,编号为TIP0~TIP3 传感器,将其与基准传感器形成一定的夹角分别安装在传感器安装支架上。由此传感器布局图,如图3 所示。

图3 传感器布局图
在Simulink 中模拟叶尖定时测量原理,如图4 所示,令叶片旋转到激光转速传感器J0 时的t=0,即该时刻为初始时间。转子角速度ω=2πfv(fv为转子转速频率),因为叶片旋转为周期性运动,可用正弦函数关系表述,所以,当电涡流传感器可以检测到某个叶片的振动信号时,等式αi=2πfv*t成立,因此用sin(2πfv*t)=sin(αi)的成立与否来断定叶片顶端经过电涡流传感器的时间,当上述等式成立时,叶片顶端到达电涡流传感器,图4 中的YTIP=y,若等式不成立时,说明叶片顶端没有到达传感器,此时令电涡流传感器输出值YTIP=0。最后将图2、图3 与图4 相关联,本文采用的叶盘结构具有8 个叶片,且采用4 支电涡流传感器对叶片振动进行测量,由此可建立8 叶片测振系统模型,如图5 所示。

图4 叶尖定时测振原理模拟图
2 失谐叶盘动频分析与参数拟合
2.1 失谐叶片-轮盘动频分析
由图1 的8 叶片-轮盘振动系统模型可知,本文采用的叶盘系统为8 叶片-轮盘结构,因此编号8个叶盘分别为NO0~NO7。在谐调叶盘系统结构为叶盘系统中各叶片材料、几何参数均相同。而对于失谐叶盘系统结构,可通过改变叶盘系统中各叶盘的材料、几何参数,使各叶片材料、几何参数不相同,即为失谐叶盘系统,由此,本文通过改变叶盘的弹性模量使8 叶片-轮盘系统达到失谐的目的,所设定的材料及材料参数如表1 所示。
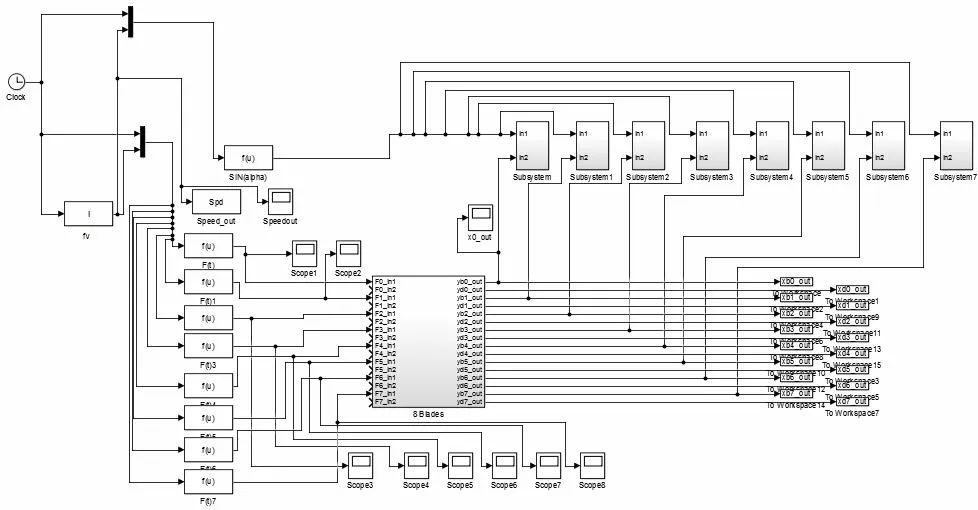
图5 8 叶片测振系统模型
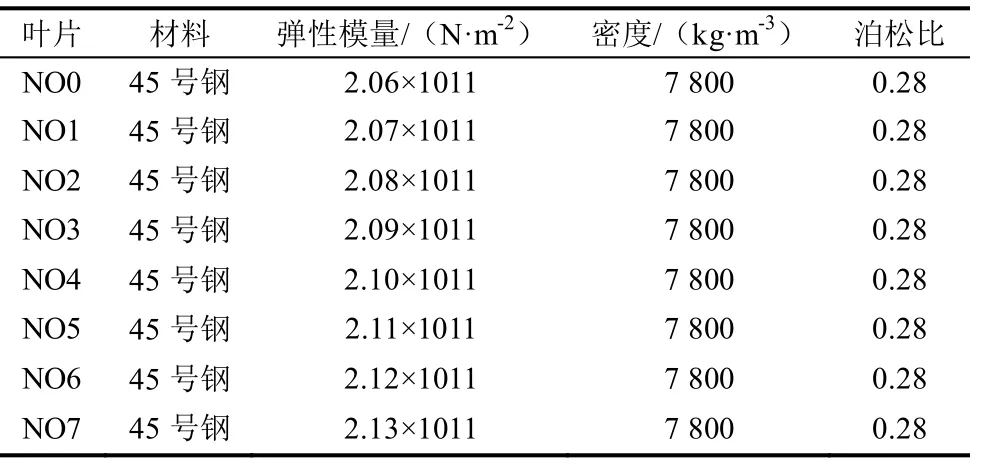
表1 叶片轮盘材料及材料参数
建立8 叶片-轮盘系统的有限元模型,并利用有限元对其进行不同转速下的动频分析,转速频率设置为0~200 Hz,为确保进行曲线拟合时的计算精度,令转速频率步长为40 Hz,进行有限元动频分析后NO0 号叶片在不同转速下的叶片振动阵型图。如图6 所示。通过此图,可以获取NO0 号叶片在不同转速频率下的固有频率。


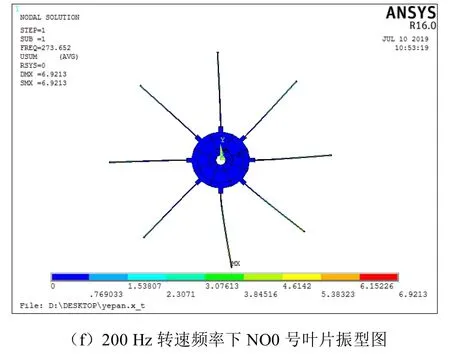
图6 不同转速频率下NO0 号叶片振型图
同理,根据上述做法,可以得出另外7 个叶片,即NO1~NO7 号叶片在0~200 Hz 转速频率下的叶片振动振型图,据此,将NO0~NO7 号叶片在不同转速频率下的固有频率汇总,可得出8 叶片在不同转速频率下的动频,如表2 所示。
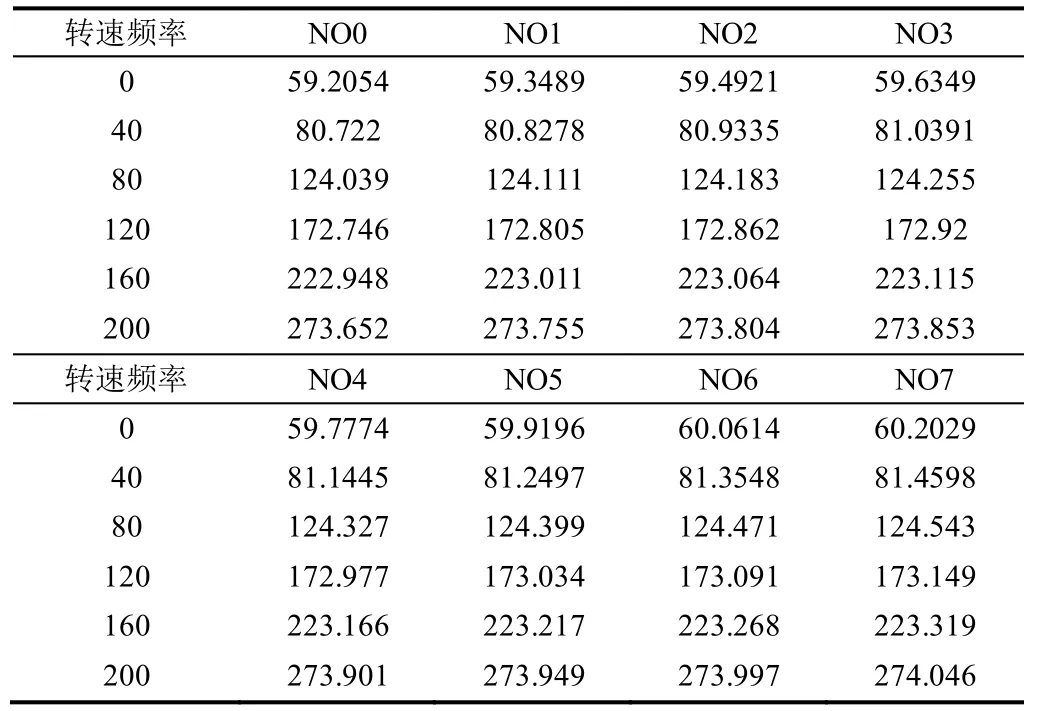
表2 8 叶片在不同转速下的动率 (Hz)
2.2 数据拟合
根据表2 的NO0~NO7 号叶片在不同转速频率下的动频,通过MATLAB 数据拟合功能拟合出叶片动频fi(i=1,2,…7)随转速频率fv变化的公式。如式(7)所示。

根据上述数据拟合结果,可绘制NO0 号叶片振动坎贝尔图,如图7 所示。

图7 NO0 号叶片振动坎贝尔图
从中可以看出,当激励倍频为1 时,NO0 号叶片不会发生共振现象,当激励倍频为2、3、4 时,NO0 号分别在转速频率为44.77 Hz、23.4 Hz、15.96 Hz 时会发生共振现象。
3 信号仿真分析与参数辨识
3.1 恒速时叶片同步振动信号仿真分析

查阅资料,取该叶片材料45 号钢的阻尼系数为0.005,由此可以求出c0=c1=…=c6=c7=0.287 N·s/m,叶片的质量为m0=m1=…=m6=m7=0.287 kg,在本文所采用的的叶盘系统模型中,相邻叶片之间无任何部件连接,叶片之间无耦合,即k01=k12=…=k67=k71=0,c01=c12=…=c67=c71=0。叶片发生同步振动时,满足f=Nefv,Ne为激振倍频,且Ne为正整数,因此在8 叶片叶尖定时测振系统模型中,叶片受到的激振力为F(t)=FAcos(2πNεfvt+φ)。令Ne=2,初始相位角φ0=0,恒偏量C=0,激振力幅值为FA=0.163 N。将TIP0~TIP3 四支叶尖定时传感器按照0°、14°、29°和43°分布安置,从上述图7 的坎贝尔图可知,当振动激励倍频为2 时,NO0 号叶片在44.77 Hz 转速频率时发生共振现象,因此,将转速频率设置为44.77 Hz,仿真时间5 s,利用8 叶片测振系统模型进行仿真,求解后可以得出恒速时NO0号叶片同步振动响应图与各传感器测得的NO0 号叶片同步振动位移图,如图8、图9 所示。

图8 恒速下NO0 号叶片同步振动响应
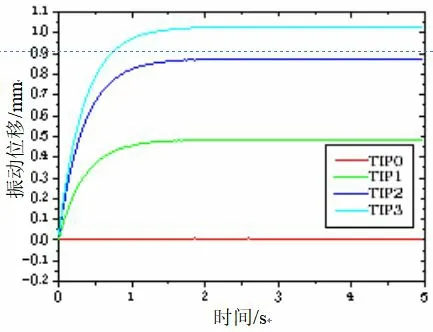
图9 恒速下各传感器测得NO0 号叶片同步振动位移
从图8 中可看出当叶片振动趋于稳定时,其振动位移为1.03 mm,而从图9 可以得出各传感器测得NO0 号叶片振动位移,其稳定振动位移参数如下表3 所示,其结果用于恒速下叶片同步振动参数辨识。

表3 各传感器测得振动位移
3.2 恒速下叶片同步振动参数辨识
将传感器数量设置为n,旋转叶片顶端经过叶尖定时传感器的时刻为ti,且叶片同步振动的振动频率ω=NeΩ,因此,恒速下不同传感器测得的叶片同步振动位移表达式为:

令采用叶尖定时传感器的数量设置为n,因此在式(9)中,i=0,1,2…n。
叶片顶端经过TIP0 传感器的时刻设置为t0=0,则4支电涡流传感器与TIP0电涡流传感器之间的安装角度差为αi=Ωti,则TIP0 电涡流传感器安装角度α0=Ωt0=0°,将αi代入到上式(9)中,可以得到:

将式(10)展开后可写成:

结合采用的传感器数量,可将n支电涡流传感器测得的叶片同步振动位移改写为:

将式(12)写成矩阵形式Y=BX,分别令其表达式如下:

由公式Y=BX中B、X 的矩阵表达形式可知,该计算公式中含有Ne、A、φ和C4 个振动参数未知,因此在Y的表达式中至少需要4 支叶尖定时传感器测得的叶片振动位移值。将Ne设定取值范围,将其在取值范围内进行倍频遍历,将可能的Ne取值代入到公式Y=BX中,通过最小二乘法求得其对应的解向量Xk:

将Nek作为遍历倍频,且Nek=1~20,因此当残差的方差Sk取得最小值时,叶片振动遍历倍频与实际倍频相等,即Nek=Ne*,从而可求得相对应的X*,对此,为得出实际激励倍频Ne*,需求得计算出的位移结果与测量的位移值之间的残差,并计算其残差的方差Sk,计算方法与求得公式如下:
将Xk代入到Y=BX中,计算其与测得的振动位移Y之间的残差Ek:

在式(17)中,Ek是由eki组成的列向量,即Ek=(ek0ek1ek2…ekn-1)T。
用残差Ek的方差Sk来表示遍历结果与测量结果的误差:
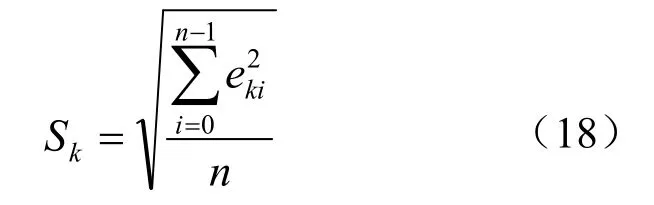
综上所述,可以列出恒定转速下叶片同步振动参数的计算公式,其公式如下所示:
振幅A:

初相位φ:

恒偏量C:

将 TIP0~TIP3 四支叶尖定时传感器按照α0=0°、α1=14°、α2=29°、α3=43°的角度差进行布置,利用表3 的恒速下4 支叶尖定时传感器测得的NO0 号叶片振动位移结果,对NO0 号叶片的同步振动参数进行参数辨识,遍历倍频取1~20,得到其参数辨识曲线如图10 所示,其中1~10 遍历倍频下的参数辨识结果如表4 所示。

图10 恒速下NO0 号叶片同步振动参数辨识曲线
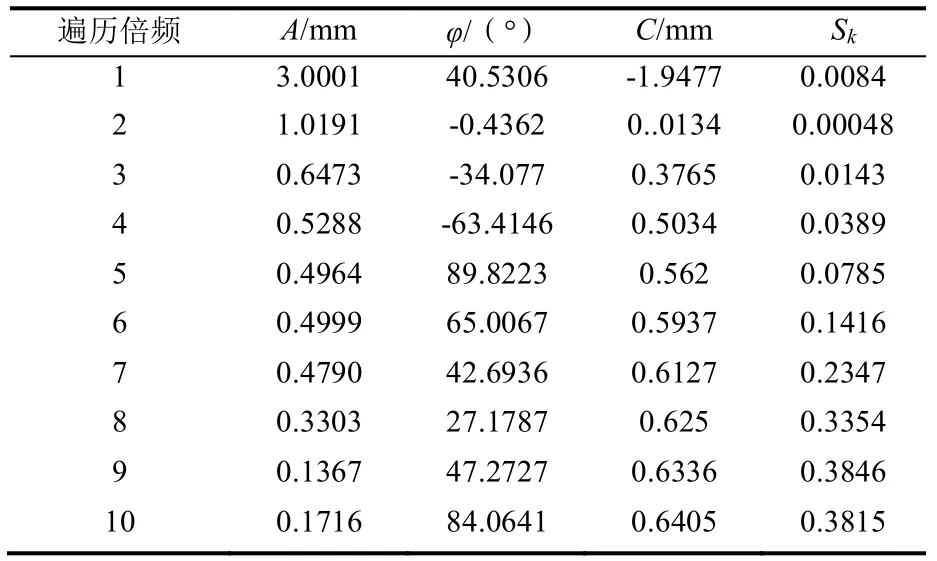
表4 参数辨识结果
由图7 的NO0 号叶片同步振动参数辨识曲线可知可以看出,Sk的最小值为0.00048,且当Sk取得最小值时,激励倍频Ne=2,因此实际振动激励倍频为2,这与恒速下叶片同步振动信号仿真时设定的激振倍频一致,由该种辨识算法计算后得到的振动参数为:振幅A=1.0191 mm,初相位φ=-0.4362°,恒偏量C=0.0134 mm。在恒速下叶片同步振动信号仿真时的振动参数为:振幅A=1.03 mm,初相位φ=0°,恒偏量C=0 mm。将此两组参数进行对比,振幅的绝对误差为0.0109 mm,恒偏量的绝对误差为0.00134 mm,初相位的绝对误差为0.4362°,各参数之间绝对误差均极小,说明利用考虑转速影响的叶盘系统仿真模型得出测量结果的准确性。
5 结论
通过对叶片振动进行理论推导,并结合叶尖定时测振原理与传感器的布置方式,建立8 叶片叶尖定时测振系统模型;对失谐叶盘系统进行有限元动频分析,得出动频随转速频率变化的关系式,据此计算出叶片刚度,绘制NO0 号叶片振动坎贝尔图,通过坎贝尔图可知,当转速频率为44.77 Hz 时,NO0号叶片会发生共振现象;因此,在恒定44.77 Hz 转速频率时对NO0 号叶片进行叶片同步振动信号仿真分析,得出叶片振幅值与各传感器测得的振动位移;由此进行恒速下叶片同步振动参数辨识,得出较为全面的叶片振动参数,将辨识结果与恒速下叶片同步振动信号仿真得到振动参数进行对比,两者相差极小,说明该种考虑转速影响对叶片振动系统进行建模仿真的测量方法是准确的,因此,该种考虑转速影响对叶片轮盘系统进行振动仿真分析的方法,为叶片振动测量提供了一种更加贴合实际的测量方式。

