深证综指的ARMA-GARCH 模型实证分析
王 莉
(南京财经大学应用数学学院,江苏南京210023)
波动性研究从Fama 建立随机游走模型,第一次用动态模型来刻画股价的波动开始。 后来被人们更广泛应用的是自回归条件异方差(ARCH)模型,由Engle 于1982 年首次提出,Engle 开辟性地运用时间序列模型来描述和预测股指以及其他金融资产指数的波动聚集性。 但ARCH 模型在实际应用中也显露出局限性,它只适用于短期自相关的异方差函数,于是Bollerslev 在ARCH 模型基础上提出一种广义自回归条件异方差(GARCH)模型,此模型在对时间序列的波动性研究领域中颇受欢迎,尤其在金融方向。 Surya 和Wibowo 通过对东盟地区的油价波动和股票收益建立GARCH 类模型来进行实证分析。 文章以深证综指为例,结合ARMA 模型和GARCH 模型对其进行描述分析。 首先,简要分析了对数日收益率序列的基本统计特征,并检验其平稳性、自相关性和ARCH 效应;建立 ARMA-GARCH 和 ARMA-EGARCH 两个模型分别对深证综指对数日收益率序列进行拟合、描述分析,进而发现我国股票市场的波动特征。
一、 实证研究设计
(一)数据选取及基本的描述统计
文章选取了1991-04-03 至2020-01-10 共7062 个深证综合指数数据进行实证分析。 数据来源于Wind 数据库,所用软件版本为EViews7.2。 为了保证所研究的序列具有稳定性,对样本数据进行如下处理,这里,Rt代表对数日收益率,Yt代表日收盘价。

由EViews 对序列Rt的基本描述性统计结果可知,其峰度远大于正态分布的峰度3;偏度大于0,故Rt序列的分布呈“尖峰右长拖尾”状,P值为0.00000,拒绝服从正态分布的原假设,因此不能随意地用正态分布来拟合深证综指对数日收益率的分布,需要对这一序列做进一步的实证分析。
(二)平稳性及自相关性检验
1. 平稳性检验
检验序列是否平稳和非随机是对其进行建模和分析前所必做的第一步。 文章使用 ADF 检验(augmented Dicky-Fuller test)来检测Rt序列的平稳性,得到ADF 检验的t统计量值为-25.08870,在1%、5%、10%的显著性水平下,均低于临界值-3.431099、-2.861755、-2.566927,P值为0.0000,故拒绝序列存在单位根的原假设,即认为Rt序列具有平稳性。
2. 自相关性检验
文章通过对自相关函数的分析来完成对Rt序列的自相关性检验。 由检验结果得,无论是序列的自相关系数(AC)还是偏自相关系数(PAC),它们的值都接近于0,Q统计量值也随着滞后阶数的增加而增大。 由于P值均为0.000,故拒绝原假设。 因此认为该序列为非随机序列,即序列值之间存在自相关性,且是长期自相关。
又Rt序列的AC 和PAC 值在滞后一期后开始递减,后面虽有波动现象,但总体是递减的,且根据AIC 判断准则,结果发现ARMA(1,1)模型拟合效果最佳,建立的均值方程如下:

其中,εt为随机误差项,参数η、λ分别为AR(1)项和 MA(1)项,由ARMA(1,1)模型拟合结果,可以写出估计的均值方程为:
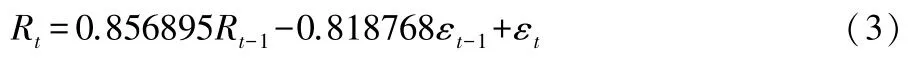
(三) ARCH 效应检验
现检验ARMA(1,1)模型拟合的均值方程(3)的残差项是否具有ARCH 效应。 由滞后1 期的ARMA(1,1)拟合模型残差项的ARCH 效应检验结果可知,其P值为0.0000,于是得出:在显著性为1%、5%、10%的水平下,都应拒绝原假设,即认为模型中存在ARCH 效应。 因此对深证综指对数日收益率Rt序列可以考虑建立GARCH 模型继续深入分析。
二、 实证研究与结果分析
(一)GARCH 模型
GARCH 模型因为具有记忆时间长和滞后结构灵活等优点,被广泛运用于描述和预测金融市场波动性。 在对波动性进行实证研究的过程中,一般选取GARCH(1,1)模型进行拟合。
由拟合结果可知,当显著性水平为0.05 时,ARMA(1,1)和GARCH(1,1)两个模型拟合的所有系数的P值均为0.0000,具有较高的显著性,在这方面可以认为,ARMA(1,1)-GARCH(1,1)模型拟合效果较好,得到的均值-方差方程分别为:

在方差方程中,可算得GARCH 项(ht)和ARCH 项(ε2t)系数之和为0.994969,小于1,满足参数约束条件。 且由于系数之和接近于1,表明当深证股市市场受到冲击时,带来的动荡虽然会衰减,但影响会较持久。
由ARMA(1,1) -GARCH(1,1)拟合模型残差项的ARCH-LM 检验结果可知,其P值明显大于显著性水平0.05,应接受原假设,故可以认为残差项中不存在ARCH 效应,由此表明ARMA(1,1)-GARCH(1,1)模型明显地消除了序列的异方差性。
(二)EARCH 模型
由于EARCH 模型对参数值的要求可正可负,适用于非对称性的描述,故文章运用EARCH 模型进行辅助验证,以便可以更好地说明我国深证股市市场风险的波动状况。
由模型的参数估计结果可知,各参数估计的Z 统计量检验都较显著。 EARCH(1,1)模型中,非对称项的系数C(5)=-0.023654,小于0,表明序列Rt存在着杠杆效应,即在其他条件相同的情况下,利空消息对深证股市的影响大于利好消息对其的影响。 根据非对称效应参数C(4)+C(5)=0.187495可知,当市场出现利好消息时,其对序列Rt的条件方差的影响为0.187495 倍;同理,C(4)-C(5)=0.234803,即利空消息对Rt序列的条件方差会造成0.234803 倍的冲击。 拟合后的ARMA(1,1)-EARCH(1,1)模型其均值-方差方程分别为:
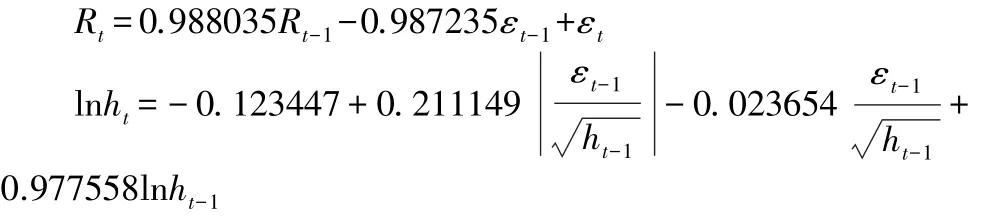
其中,ht为t期的预测方差项。 检验 ARMA(1,1) -EARCH(1,1)模型是否存在条件异方差性,结果显示,在显著性水平为1%时,ARMA(1,1)-EARCH(1,1)模型的残差可以认为已经消除了异方差性,但效果并不显著。
现比较两个模型的评价标准,结果如表1 所示。

表1 模型评价标准的比较
比较表中的数据可知,两组模型的评价标准值相差很小,但是 EGARCH(1,1)模型的 AIC、SC 和 HQC 值全部小于GARCH(1,1)模型对应的值,即相较 ARMA(1,1)-GARCH(1,1)来说,ARMA(1,1)-EGARCH(1,1)模型拟合得相对较好。 但 ARMA(1,1)-EGARCH(1,1)模型的异方差效应远小于 ARMA(1,1)-GARCH(1,1)模型,故综合考虑,ARMA(1,1)-GARCH(1,1)模型更适合对对数日收益率Rt序列进行拟合与分析。
三、 结论
基于以上实证分析,文章可以得出如下结论:①深证综指对数日收益率具有波动聚集性。 其均值大于0 而接近于0,表明股票市场的投资回报率较低。 又偏度大于0,说明深证综指对数日收益率分布是右拖尾的,说明我国深证股票市场已趋于相对成熟。 ②对深证综指对数日收益率建立的ARMA(1,1)-GARCH(1,1)模型较好地消除了序列中的ARCH 效应。 ③基于GARCH 模型估计的方差方程中,ARCH项和GARCH 项的系数之和小于1 且接近于1,表明深证综指的冲击波动随时间会衰减,但以后冲击可能持续较多期。④综合对比分析 ARMA(1,1)-GARCH(1,1)和 ARMA(1,1)-EGARCH(1,1)两组模型,可以发掘出深证综指对数日收益率的更多特征,且研究发现对深证综指对数日收益率建立ARMA(1,1)-GARCH(1,1)模型效果更好。 ⑤深证综指对数日收益率具有较明显的负向非对称性,即等额度的利空消息比利好消息对深证股市市场的冲击更大。

