我国区域经济发展差异的全要素生产率分析——基于DEA模型的Malmquist指数视角

张 朝

（工业和信息化部中国电子信息产业发展研究院，北京100846）

一、引言

1.研究背景

在党的十九次全国代表大会上，习近平总书记提出全新论断，“我国社会主要矛盾已经转化为人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾”。我国当前发展的不平衡不充分，一个突出的表现就是区域经济发展不平衡。我国不同区域间经济存在的巨大差异一直是困扰经济社会发展的一大障碍，尤其是20世纪90年代以来，差距扩大愈加明显（王小鲁、樊纲，2004），已成为亟待解决的重要问题。

造成区域经济差异过大的原因有很多，例如地理位置、资源禀赋、生产要素、制度环境等。过去，学界主要将造成区域发展不平衡的因素归结为资源禀赋以及生产要素的投入等，但随着研究的持续深入，不论是国内还是国外的相关研究，越来越多的学者将区域经济差异化的主要原因，从资本、劳动等生产要素的投入，转移到全要素生产率上。有的学者认为应当有更多针对于全要素生产率的测算(Easterly，Levine，2001)，用以解释区域经济发展差距。有的学者对新古典增长模型进行了修正，研究后发现对于任何资本变量的任何修正，都不能解释不同区域，尤其是不同国家之间存在的巨大收入差距，所以得出结论只有全要素生产率才能解释差距产生的原因(Prescott,1998)。与Prescott持相同观点的，还有Hall &Jones(1999)、Klenow&Rodriguez-Clare(1997)。与国外的研究类似，我国对于区域经济差异化的研究，重心也从生产要素的投入逐渐转向各地区不同全要素生产率的分析。也有越来越多的国内学者认为，全要素生产率的差异才是造成我国区域间巨大差异的主要原因（彭国华，2005；李静等，2006；郭庆旺等，2005）。

文章在对我国省际数据进行整理分析的基础之上，利用基于DEA模型的Malmquist指数法，测算出2000年我国区域协调发展政策正式实施以来，各地区全要素生产率的变化情况。然后以东部、中部、西部和东北部为单位，分析其经济技术效率以及全要素生产率变动情况，最后根据模型得出的结论，给出相应的对策建议。

2.模型选择

目前，基于全要素生产率的测算主要有索洛余值法、隐性变量法和Malmquist指数法。

（1）索洛余值法

索洛余值法也是目前测度全要素生产率使用较多的一种方法。索洛认为，全要素生产率可以用产出增长率减去要素投入增长率即资本、劳动后的贡献来表示。设总量生产函数为柯布-道格拉斯生产函数：

其中，Yt为实际产出，At为技术水平，Lt为劳动投入，Kt为资本投入，α，β分别是劳动和资本的产出弹性。全要素生产率增长率表示为：

对方程(1)两边取自然对数：

对α、β做正规化处理：

在Yt、Lt、Kt已知的条件下,由方程式(3)可以计算出α、β，带入方程式(2)，求出全要素生产率，即：

其中，a为全要素生产率增长率，y为实际产出增长率，l为劳动增长率，k为资本增长率。

索洛余值法更关注函数的相关性质，且计算简便，易于操作，因此这一计算全要素生产率的方法具有广泛的适用性，但索洛余值法也具有明显的缺陷。在索洛模型中，技术进步的贡献率只是简单的用产出增长率减去劳动、资本增长率来表示，这样的计算明显过于简单，因为索洛余值中包含了除劳动、资本以外的所有因素，显然不仅仅是技术进步贡献率。

（2）隐形变量法

隐性变量法强调全要素生产率是一个不可观测的变量，因此应当在数据平稳性和协整检验基础之上，选用状态空间模型做极大似然估计来测算全要素生产率。假定规模报酬不变，设定柯布-道格拉斯生产函数：

其中，lnTFPt表示全要素生产率的增长率。假设lnTFPt是一个隐形变量，且遵循一阶自回归过程，则有：

其中，ρ为自回归系数，满足|ρ|＜1，μt为白噪声。利用状态空间模型，通过极大似然估计法，同时估算出状态方程和观测方程，最后估算出全要素生产率。

隐形变量法的优点在于将全要素生产率作为一个独立的状态变量从残差中分离出来，相对于索洛余值法更加精确，但是隐形变量法在理论上仍然是建立在新古典理论基础之上，采用柯布-道格拉斯生产函数，且假定规模报酬不变，所以虽有改进但本质不变。

（3）基于DEA模型的Malmquist指数法

Malmquist指数最初由Malmquist(1953)提出，他利用缩放因子之比构造了消费数量函数。随后Caves等(1982)将Malmquist的思想运用到生产分析中，通过距离函数构建生产率函数，并称其为Malmquist生产率指数，但初期由于缺乏测度距离函数的具体方法，所以当时Malmquist指数更多的是作为一种理论指数存在。

直到Charnes等(1978)因为提出数据包络分析法(DEA)，使得距离函数的测度方法得到了极大的拓展，并逐渐成为生产分析过程的重要方法。数据包络分析(DEA)是一种非参数估计方法，与前两种测算方法相比，其优点在于不用提前设定具体的函数形式来得到前沿函数。随后基于数据包络分析法，Fare(1989、1994a)将Malmquist指数应用到生产率研究领域，并将Malmquist指数从理论指数变成了实证指数，具体形式如下：

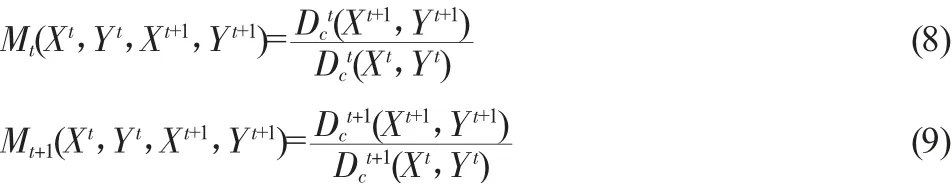
其中，Dct和Dct-1分别表示以t时的技术水平为参照，在规模报酬不变的条件下，t和t+1时期的距离函数，(Xt，Yt)、(Xt+1，Yt+1)分别表示t和t+1时期的投入和产出向量。Malmquist指数可以表示为：

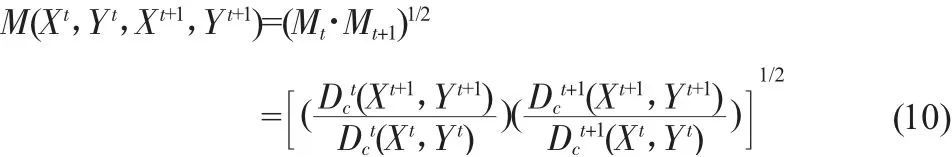
如果测算后该指数小于1，表明从t时期到t+1时期，全要素生产率是下降的。如果该指数大于1，则表明从t时期到t+1时期，全要素生产率是上升的。Malmquist指数可以分解为技术进步指数(TC)和技术效率变化指数(EC)。技术效率变化指数（EC)又可进一步分解为规模效率指数(SEC)和纯技术效率指数(PEC)。具体形式为：

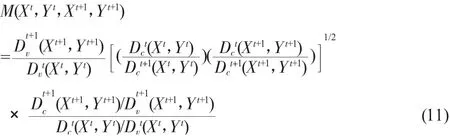
在这其中，

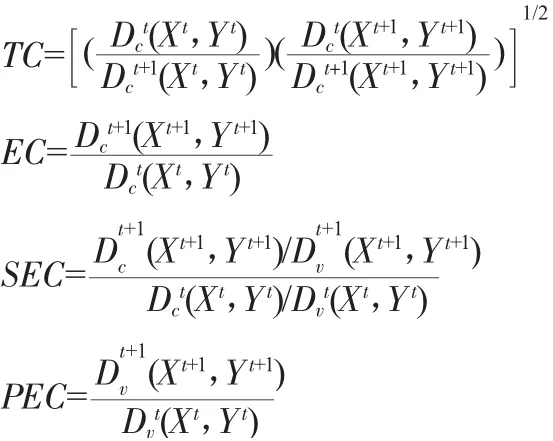
其中，Dc(X，Y)为规模报酬不变条件下的距离函数，Dv(X，Y)为规模报酬可变条件下的距离函数。

在数据包络分析方法中引入Malmquist指数法具有以下优点，一是不需提前设定具体的函数形式，限制较少；二是可以对资源配置效率和全要素生产率进行再分解，从而找出影响资源配置效率和全要素生产率变化的最主要因素。基于以上原因，此方法已被越来越多的学者采用。因此，本研究也选用基于DEA模型的Malmquist指数法来测度全要素生产率的变化率。

二、模型的变量选择与数据来源

1.变量选择

基于DEA模型的Malmquist指数法不需提前设定具体的函数形式，但需有投入变量、产出变量以及距离函数。目前大多数学者都选用劳动、资本作为投入变量，总产出作为产出变量。文章选取劳动力水平、资本存量作为投入指标，国内生产总值作为产出指标，以31个省区市作为决策单元，探究各地区的全要素生产率变化水平，为了处理方便，研究参考李国彰等(2010)、章祥荪等(2008)的处理办法，为保持口径一致，将重庆纳入四川省的统计范畴。最后，为保证研究的稳定性和连续性，文章选择各地区2000-2017年相关的面板数据作为样本数据。之所以选择2000年以后的数据主要基于以下两方面原因：一是一般情况来说，我国在1999年以后工业化逐渐趋于成熟，并进入稳定增长阶段。二是我国推进区域发展的各项国家战略，如西部大开发、中部崛起、振兴东北老工业基地战略等，均在2000年以后正式提出，可以通过文章结论，检验我国区域发展战略的实施效果。

（1）产出指标

一般而言，产出水平的衡量一般选用国内生产总值，这也是目前国际上的通行做法，因此文章也采用各省区市的国内生产总值来衡量我国的区域产出水平。由于各年度的价格水平不同，不加处理会对模型的结果产生影响，因此文章选用各地区GDP平减指数，以2000年为基期进行指数平减，以得到各地区当年的实际GDP。

（2）劳动投入

对于劳动投入这个变量的选取，目前普遍采用的是就业人员数量。文章也按照这个标准，用就业人员数量来衡量各地区的劳动投入，具体则以按三次产业分的从业人员数量来表示。

（3）资本投入

对于资本投入变量的选取，目前普遍采用资本存量来表示，而资本存量的计算方法较多，经常使用的是Goldsmith(1951)提出的永续盘存法。永续盘存法主要涉及三个变量，即基期资本存量、当年投资额以及折旧率。文章选用学界普遍使用的全社会固定资产投资来衡量各地区的资本投入，公式为：

Kt为各地区t时期的全社会固定资产总值，Kt-1为各地区t-1时期的全社会固定资产总值，δ为折旧率，It为t时期的固定资产投资额。

文章参照大多数研究省级资本存量的文献，采用张军、吴桂英(2004)等测算的各省区市2000年的资本存量作为基期数值，折旧率也采用9.6%，固定资产投资指数采用各地区数值并以2000年为基期进行平减，固定资产投资额选用当年固定资本形成额。

2.数据来源

各省区市2000-2017年的国内生产总值、国内生产总值指数、固定资本形成额和固定资本投资价格指数的数据来自国家统计局，就业人员数据来自中国人口与就业统计年鉴以及各省历年统计年鉴，部分省份以及年份有数据缺失者以wind数据库以及各省相应年份的统计年鉴数据补齐。

三、我国区域经济发展差异的实证分析

1.区域经济技术效率的差异分析

（1）测算结果

基于CCR模型和BCC模型，选用面板数据测得我国2000-2017年的经济综合技术效率、纯技术效率和规模效率，表1给出历年的测算结果。

（2）差异分析

技术效率是指以考察当期所确立的生产前沿为参照，经过计算而得的，所以此值是当年既定生产技术条件下的技术效率水平。如果效率值等于1，说明在当年的技术水平下，投入产出效率达到最优。如果效率值小于1，则说明当期的有效产出仍可扩大一定比例或者投入要素仍可缩减一定比例。根据数据运行结果，只有北京、广东、天津三省市数值为1，说明仅就技术效率而言，只有上述三个地区投入产出效率达到最优。进一步分析表1的测算结果，可以得出如下结论：

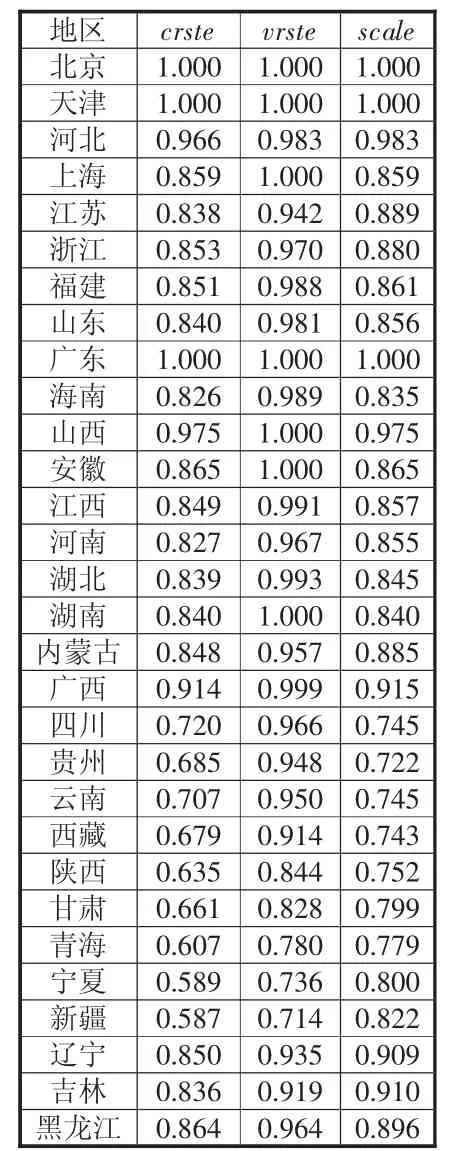
表1 2000-2017年各省区市经济技术效率及构成测算结果

第一，2000-2017年间，我国区域经济效率仍是大致呈现自东向西阶梯递减的区域分布特征，其中东部地区综合技术效率为0.903，纯技术效率为0.985，规模效率为0.916；中部地区综合技术效率为0.866，纯技术效率为0.992，规模技术效率为0.873；东北地区综合技术效率为0.85，纯技术效率为0.939，规模技术效率为0.905；西部地区综合技术效率为0.694，纯技术效率为0.876，规模技术效率为0.792。就综合技术效率而言，东部地区最高，其次是中部地区，东北地区高于西部地区，西部地区的综合技术效率水平在四大区域中居于末尾，所以就资源利用效率而言，东部地区最高，中部其次，东北部第三，西部地区最低。就纯技术效率和规模技术效率而言，基本呈现与综合技术效率类似的区域分布特征，东中部地区高于东北部和西部地区。

第二，具体来看，综合技术效率排名前10位的省区有6个位于东部地区，2个位于中部地区，东北部和西部地区各只有1个，而排名后10位的省区有9个位于西部地区，1个位于东部地区，其中超过0.8的中高效率省份有21个，东部地区占比为48%，中部地区占比为29%，东北部地区占比为14%，西部地区占比为10%。因此，从静态的区域经济技术效率来看，东部和中部地区明显领先于东北部和西部地区。总体来看，东部地区处于全国最高水平，市场机制对要素的配置效率、使用效率最高，中部和东北部地区居中，西部地区则处于最低水平，要素配置效率和使用效率均需进一步改善提升。

2.区域全要素生产率的差异分析

（1）测算结果

根据投入导向模型以及各省区市数据，采用面板数据测得我国2000-2017年的技术进步变动指数、技术效率变动指数、纯技术效率变动指数、规模效率变动指数和全要素生产率变动指数，表2给出了各个地区以及全国平均的测算结果。

（2）差异分析

经测算，2001-2017年我国全要素生产率变化率为0.963，说明全要素生产率增长率总体是负值，与武鹏测算（2001-2010年）、章祥荪等测算（2001-2005年）、张煜等测算（2001-2012年）的结论（小于1）保持一致。从构成上看，技术效率指数为1.001，纯技术效率变动指数为1.0001，规模效率变动指数为1.0005，均大于1，技术效率保持增长态势，说明我国投入要素利用率、生产规模等因素提高了生产中的效率，技术进步变动指数为0.963，是我国全要素生产率变化率小于1的主要原因，这意味着我国技术所涵盖的各种知识的积累和改进以及新技术的使用不足，在技术进步方面仍具有较大的发展潜力。实证结果再次验证，自2000年以来，中国经济增长主要不是依赖新技术的研发，而是靠不断提高现有技术的利用效率以及规模效益，所以我国自主研发能力亟待提升。具体分析如下：

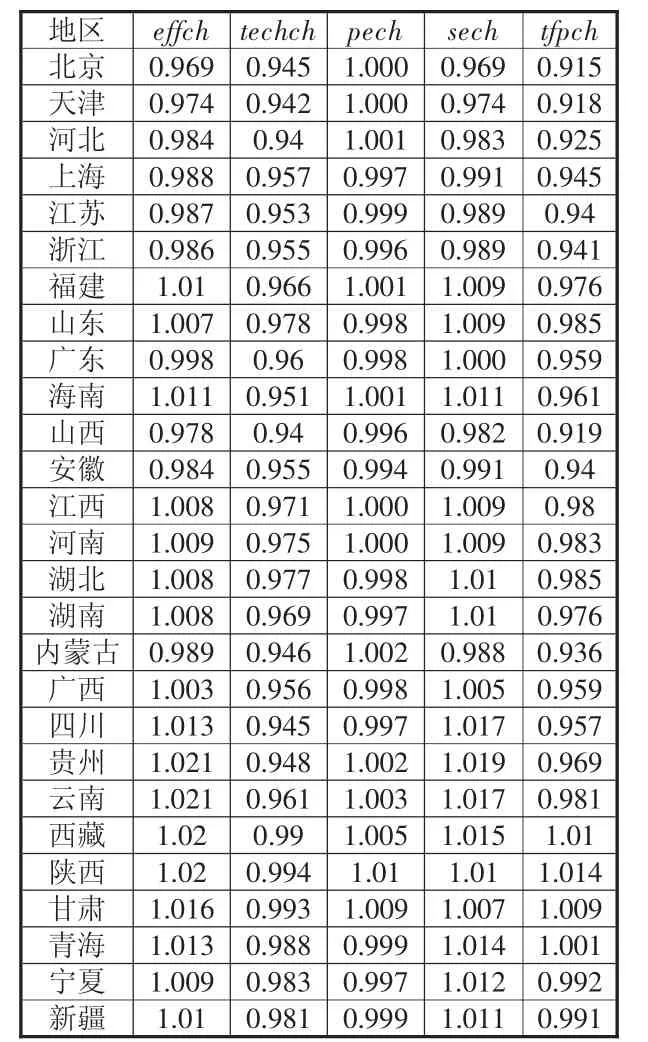
表2 2000-2017年各省区市Malmquist生产率指数及构成测算结果

第一，从考察期来看，我国全要素生产率增长率与经济技术效率不同，大致呈现自东向西阶梯递增的区域分布特征。东部地区全要素生产率变动指数为0.9465，技术效率变动指数为0.9914，技术进步变动指数为0.9547；东北地区全要素生产率变动指数为0.9493，技术效率变动指数为0.991，技术进步变动指数为0.9573；中部地区全要素生产率变动指数为0.9638，技术效率变动指数为0.9992，技术进步变动指数为0.9645；西部地区全要素生产率变动指数为0.9835，技术效率变动指数为1.0123，技术进步变动指数为0.9714；就全要素生产率增长率而言，西部地区最高，其次是中部地区，东北地区高于东部地区，东部地区全要素生产率增长率在四大区域中居于末尾。技术进步变动情况与全要素生产率增长率变动一致。

第二，具体来看，全要素生产率变化率排名前10位的省区，7个位于西部地区，2个位于中部地区，1个位于东部地区，而排名后10位的省区有6个位于东部地区，2个位于中部地区，西部地区和东北部地区则各有1个，其中增速为正的省区有4个，全部位于西部地区。技术效率排名前10位的省区有8个位于西部地区，2个位于东部地区，而排名后10位的有6个位于东部地区，2个位于中部地区，西部地区和东北部地区则各有1个，其中增速为正的省区有18个，西部地区占比为56%，东部地区占比为22%，中部地区占比为22%。技术进步指数排名前10位的省区6个位于西部地区，3个位于西部地区，1个位于东部地区，而排名后10位的省区有5个位于东部地区，3个位于西部地区，东北部地区和中部地区各有1个，对于技术进步指数而言，增长均为负。因此，从全要素生产率变动来看，与静态的经济技术效率相反，西部地区明显领先于其它地区，东部地区居于末尾。

四、结论与政策建议

1.结论

我国区域经济发展不均衡，已日渐成为困扰我国经济平稳健康发展的巨大障碍。为了解决这一难题，自2000年以来，我国相继提出西部大开发战略、中部崛起战略以及振兴东北老工业基地战略。习近平总书记在十九大报告中也指出，要“实施区域协调发展战略，建立更加有效的区域协调发展新机制”。因此，转变经济增长方式，实施创新驱动战略，提升我国全要素生产率，培育经济增长新动能，促进区域协调均衡发展成为必然选择。文章基于DEA模型的Malmquist指数法，测算了2000-2017年间，我国经济技术效率与全要素生产率增长率，并将经济技术效率分解为纯技术效率和规模效率，全要素生产率增长率分解为技术进步变化率、技术效率变化率、纯技术效率标化率和规模经济效率，得出基本结论：从经济技术效率来看，东部地区处于全国最高水平，中部和东北地区居中，西部地区处于最低水平。从全要素生产率增长率来看，与静态的经济技术效率相反，西部地区处于全国最高水平，中部和东北地区居中，东部地区最低。这也是由于我国改革开放初期即实施东部沿海开放战略，与2000年开始实施的其他地区战略相比时间较早，所以增速较低。具体来看：

第一，在经济技术效率方面，从地理区域而言东部、中部、东北部、西部地区依次递减，与我国区域经济发展状况基本吻合。东部地区是我国改革开放的前沿阵地，体制机制改革快于其它地区，各种资源要素不断集聚，人才技术等方面优势明显，经过改革开放四十多年的积累，资源配置效率、生产管理水平等方面均处于全国最高水平。西部地区相比于中部地区和东北地区，虽然具有资源优势但其产业发展基础较中部和东北部地区更为薄弱，发展起点更低，从考察期来看，其经济技术效率指数也均低于中部和东北部地区，资源配置效率全国最低。

第二，从全要素生产率增长率来看，与经济技术效率相反，呈现东部、东北部、中部、西部地区依次递增状态，即西部地区全要素生产率增速全国最高，其次是中部地区地区，东北地区位于第三，这说明我国区域协调发展政策成效已经显现。东部地区由于改革开放的前二十年增速较快，改革红利已逐渐得到释放，2000年以后增速降低。起自2000年的西部大开发战略，2003年的振兴东北老工业基地战略，以及2004年的中部崛起战略，开始逐渐显现出政策效果，落后地区全要素生产率得到了提升，相对于东部地区，西部、中部与东北部地区由于起点较低，所以相对增速较快。值得注意的是，导致区域全要素生产率增长率较低的主要原因是技术进步指数较低，这说明我国各区域对于新技术的引进与研发不足。

2.政策建议

第一，我国东部地区市场机制对资源配置的效率相对最高，西部地区最低。西部地区虽然在西部大开发战略推进下迅速发展，但由于体制机制改革相对滞后，其改革力度远远落后于东部地区，限制了其资源配置效率，造成要素使用效率的损失。因此应当进一步深化体制机制改革，尤其是对于东北地区和西部地区，坚决破除体制机制障碍，确立企业的市场主体地位，依托市场配置资源，形成一个同市场经济对接的体制机制。相关政府部门可以采取更加积极有效的方式，因城施策、因地制宜，注重合理缩小区域间劳动力成本的差距，通过引导人才等生产要素跨区域合理流动等方式，扭转当前不平衡的经济发展局面，进一步缩小区域经济差距。相信随着我国各项区域发展战略的深入推进，地区发展不平衡不充分的问题必将得到有效缓解。

第二，我国西部地区全要素生产率增速最快，其次是中部地区和东北地区，东部地区最低。所以西部地区虽然资源配置效率较低，但在考察期内，西部地区和中部地区包括技术效率指数、纯技术效率指数、规模效率指数以及全要素生产率变化率等指标基本都居于东北部和东部地区之上。这说明落后地区的经济增长动能逐渐得到激发，因此应当进一步深入推进振兴东北老工业基地战略、西部大开发战略和中部崛起战略。增长速度放缓之际，正是经济结构调整、转型升级的契机。我国大部分地区全要素生产率增速较低，主要是由于技术进步指数的影响，说明目前我国对于新技术的引进与研发仍然不足。因此在当前一方面应当继续大力引进国际先进技术，另一方面也要提高自主创新能力，加快自身创新体系的建设，在资源节约、环境友好的基础上不断提升新知识、新技能、新发明以及新的组织结构或管理在经济活动中的应用，提高人们的经济活动水平，最终促进各区域经济的创新协调发展。