全应变梯度挠曲电纳米梁有限单元法研究

陈玲玲， 杨 旭， 刘 洋， 王炳雷

(山东大学 土建与水利学院工程力学系，济南 250061)

1 引 言

压电效应是最常见的力电耦合效应,是应变ε和电极化P之间的线性耦合[1]。虽然在生活中有着广泛的应用,但压电效应不是普遍存在的。因为它只存在于非中心对称介电材料中,并且其激发还受限于居里温度Tc。

不同于压电效应,挠曲电效应是一种普遍存在的力电耦合效应,是应变梯度∂ε/∂x与电极化P之间的线性耦合。理论上,挠曲电效应存在于所有的电介质材料中,如液晶、聚合物和脂质双层膜等[2-4]。它在能量收集、传感和驱动、高级显微镜、人工肌肉和微创手术方面有广泛的应用前景[5,6]。挠曲电效应的激发没有温度限制,并且其在纳米尺度下会变得更加显著(即存在尺寸依赖性),这是因为随着结构尺寸的减小,应变梯度会相应地增大。

近些年,挠曲电效应引起了人们的广泛关注,主要原因有两个。(1) 铁电陶瓷的挠曲电效应试验表明,一些高介电常数的材料可以获得比预期更强的挠曲电特性[7]；(2) 随着先进的纳米技术和小型化趋势的发展,纳米结构材料得到了广泛的开发。挠曲电效应最重要的应用之一就是利用其尺寸依赖性而制成的俘能器[8]。同时,挠曲电效应还可以显著提高纳米梁的压电性,这为其在微纳机电系统中的应用提供了新的途径。

Kogan[9]为了在理论上解释电介质中的挠曲电效应,首次提出了挠曲电理论,并估计了挠曲电系数的取值范围。申胜平等[10]从电焓学的角度出发,同时考虑了挠曲电效应、表面效应和静电效应,严格推导出了纳米电介质的控制方程。周亚荣等[11]给出了考虑挠曲电效应的纳米欧拉梁的理论框架。王炳雷等[12]研究了考虑挠曲电效应的揉皱电介质薄膜的能量俘获机制。

应变梯度是引起挠曲电效应的直接原因,为了准确地描述微构件中的挠曲电效应,必然要引入应变梯度理论。应变梯度理论的发展已有半个多世纪,应变梯度理论最先由Mindlin[13]提出,除了 2个 Lamé常数之外,对于各向同性材料还需要额外的16个独立的材料尺度参数。Mindlin等[14]对其之前的理论进行了简化,使材料尺度参数从 16个 减少到了5个，但仍很难通过实验确定。周慎杰等[15]提出了全应变梯度弹性理论,通过对两组应变梯度张量进行正交分解,严格证明了只有3个材料尺度参数是独立的。这3个材料尺度参数l0,l1和l2分别与膨胀梯度张量、拉伸梯度张量和转动梯度张量相关。

另一方面,在挠曲电理论模型中必须考虑电极化P和应变梯度u之间的耦合,然而对于总能量来说,应变梯度弹性项(U～u·gu/2)也是至关重要的一项。但有些研究并未考虑这一项的影响。邓谦[16]的研究表明,以往的研究低估了应变梯度弹性项的影响。纳米尺度下,其影响是不可忽视的。挠曲电的尺寸效应只表明了随着结构的特征尺寸减小,其挠曲电响应会增强,却没有给出在什么条件下这种增强现象会减弱,而应变梯度弹性项可以抑制这种现象。因此,为了考虑应变梯度弹性项的影响,本文采用全应变梯度弹性理论[15]。

然而,挠曲电问题中的高阶偏微分方程常给理论求解带来困难。为此,人们开始寻求有效的数值方法。其中，有限单元法一直是解决边值问题的有效方法。王凯等[17]建立了考虑应变梯度理论的二维及三维问题的自然邻近混合伽辽金法。邓峰等[18]提出了四种二维混合有限单元来研究挠曲电效应,随后又创建了三维混合有限单元法,用来模拟挠曲电球壳和截棱锥的力电耦合行为[19]。与理论研究和实验分析相比,有关挠曲电效应的数值研究相对较少,并且挠曲电效应的有限单元法也需要高阶的有限单元来满足其连续性。

因此,为了求解纳米欧拉梁的挠曲电问题,本文提出了一种基于全应变梯度弹性理论的包含3个独立材料尺度参数的有限单元法,并通过一个简单的欧拉简支梁算例,来研究挠曲电效应和应变梯度弹性项在挠曲电问题中的影响。

2 基本理论

根据全应变梯度弹性理论,在本构关系中,除了2个经典的拉梅常数外,还引入了3个独立的材料尺度参数[15]。因此,考虑挠曲电效应的线弹性材料的内能密度函数可以表示为

(1)

在传统的电焓密度中引入挠曲电理论,则得到新的电焓密度H的表达式为[20]

(2)

式中e0=8.85×10- 12F/m为真空介电常数,Φ为电势,z为梁的厚度方向。

在整个电介质结构中,考虑挠曲电效应的哈密顿变分原理为

(3)

式中δW为外力功的变分。

3 纳米欧拉梁的理论模型

考虑一个长度为L、厚度为h、宽度为b的压电纳米简支梁中的力电耦合响应,如图1所示。以梁未变形前的中心轴为x轴,建立笛卡尔坐标系,z轴沿着梁的厚度方向。在梁的上下表面(z=±h/2)施加一个外加电压ΔV,在梁的中点处(x=L/2)施加一个集中力F。当施加电压ΔV时,简支梁会在z方向产生机械变形；当施加集中力F时,简支梁会在z方向产生电极化。在下面的推导中,坐标(x,y,z)由(1,2,3)表示。

设弯曲梁的z向位移为w(x),则欧拉梁中任意一点的位移可以表示为

u1(x,z)=-z(∂w(x)/∂x)u2(x,z)=0u3(x,z)=w(x)

(4)

图1 简支梁力电耦合响应

the simply supported beam

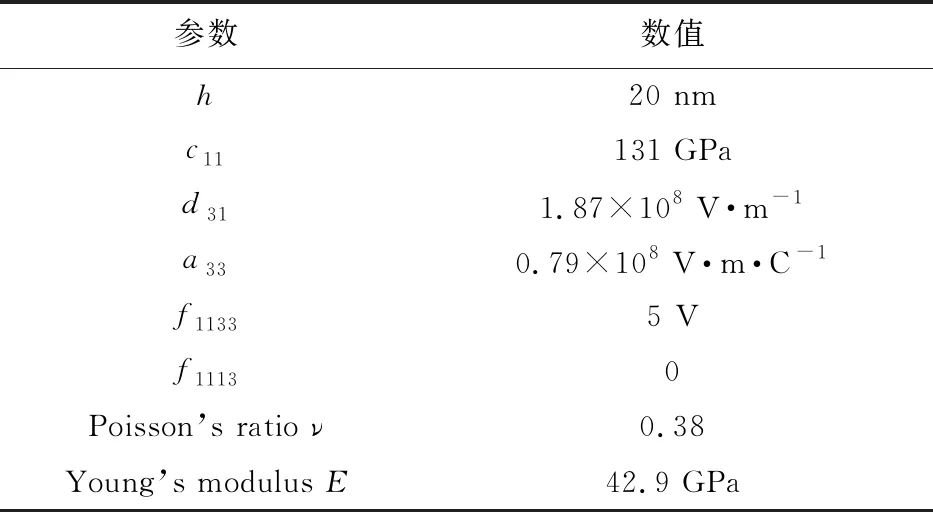
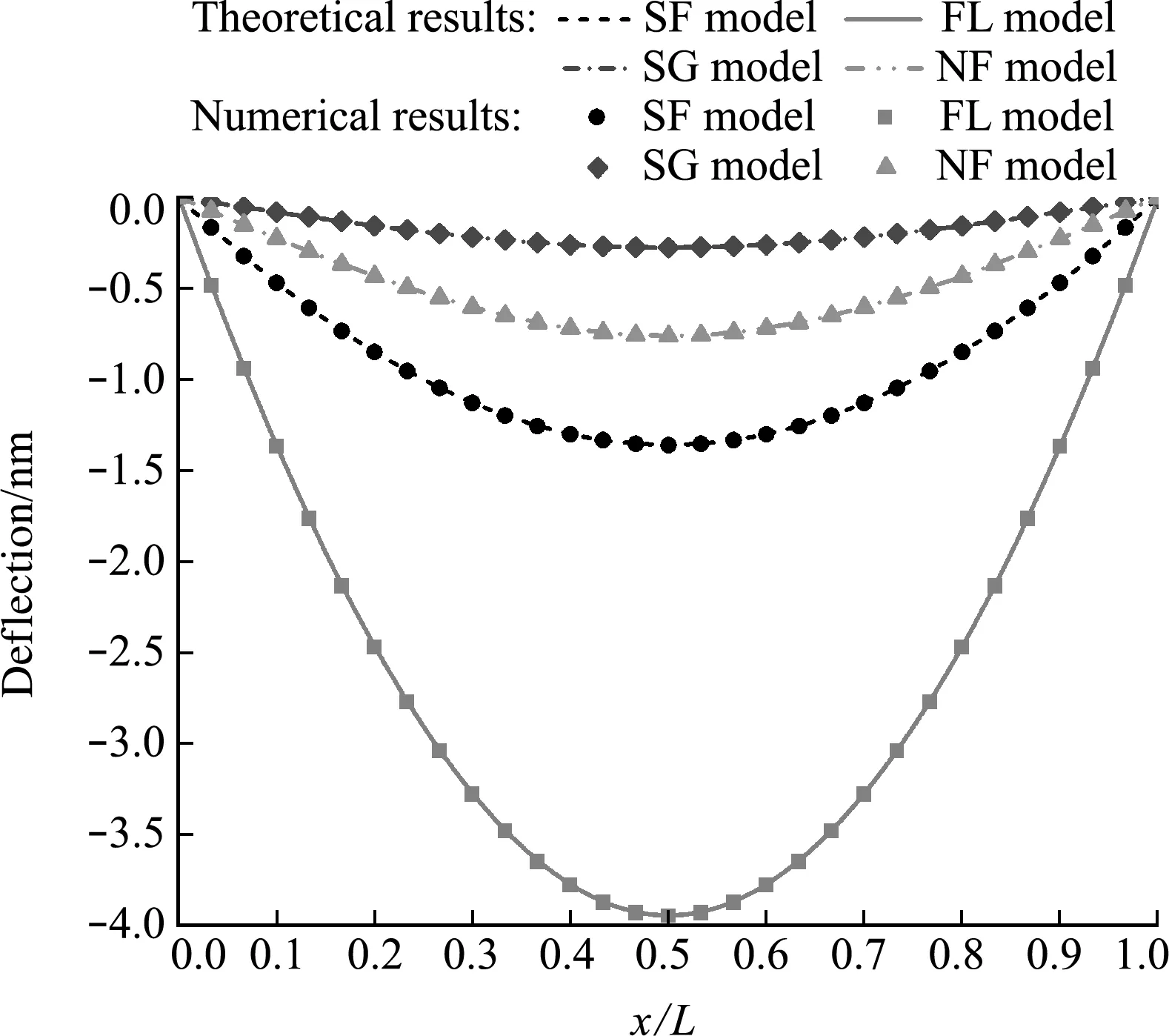
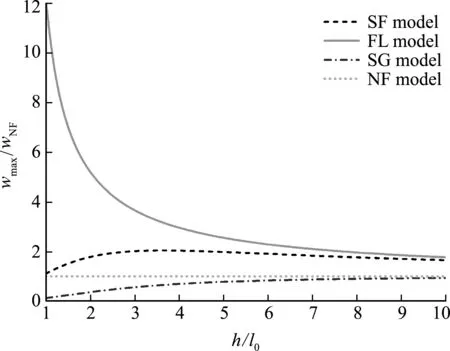
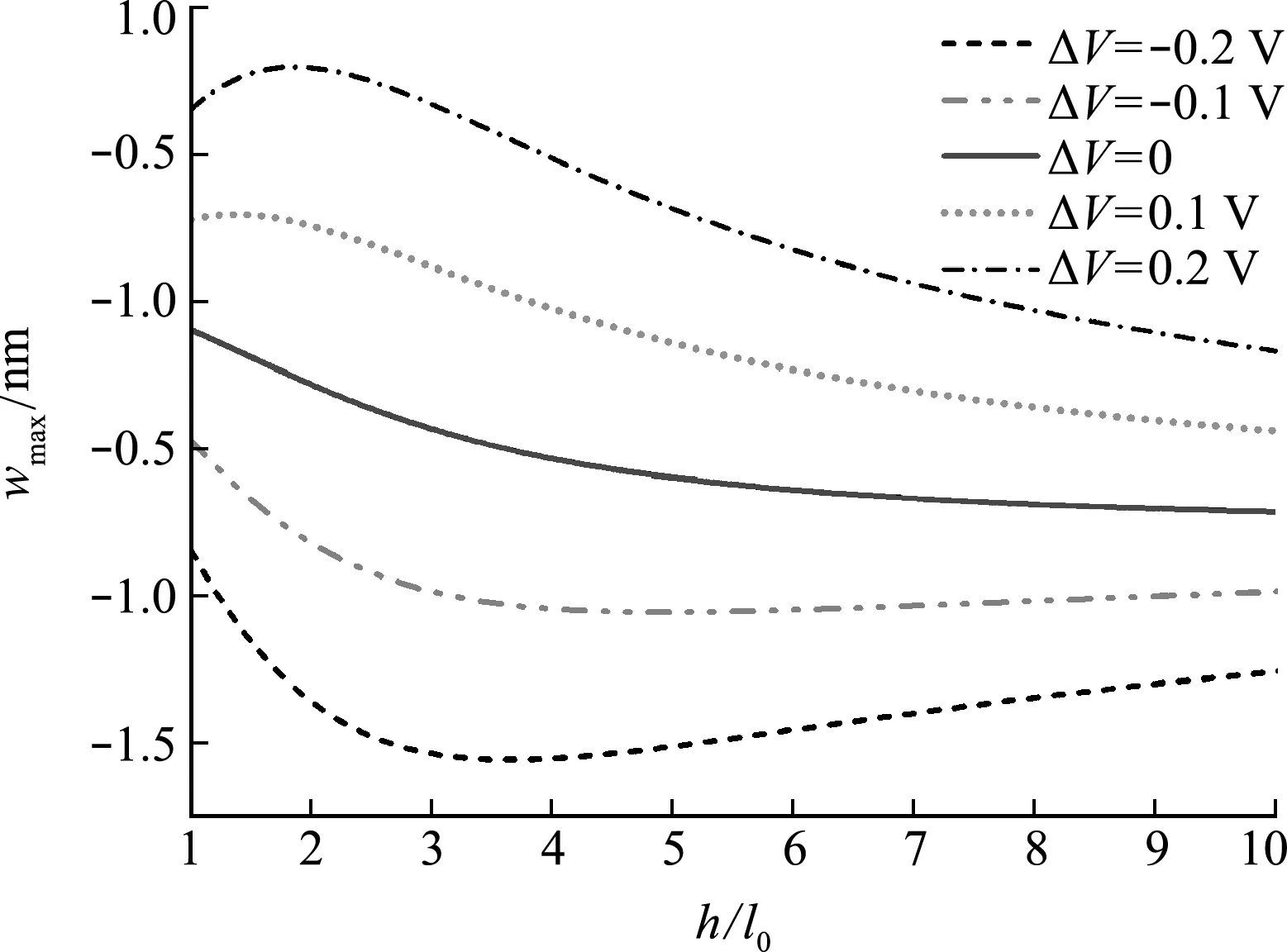
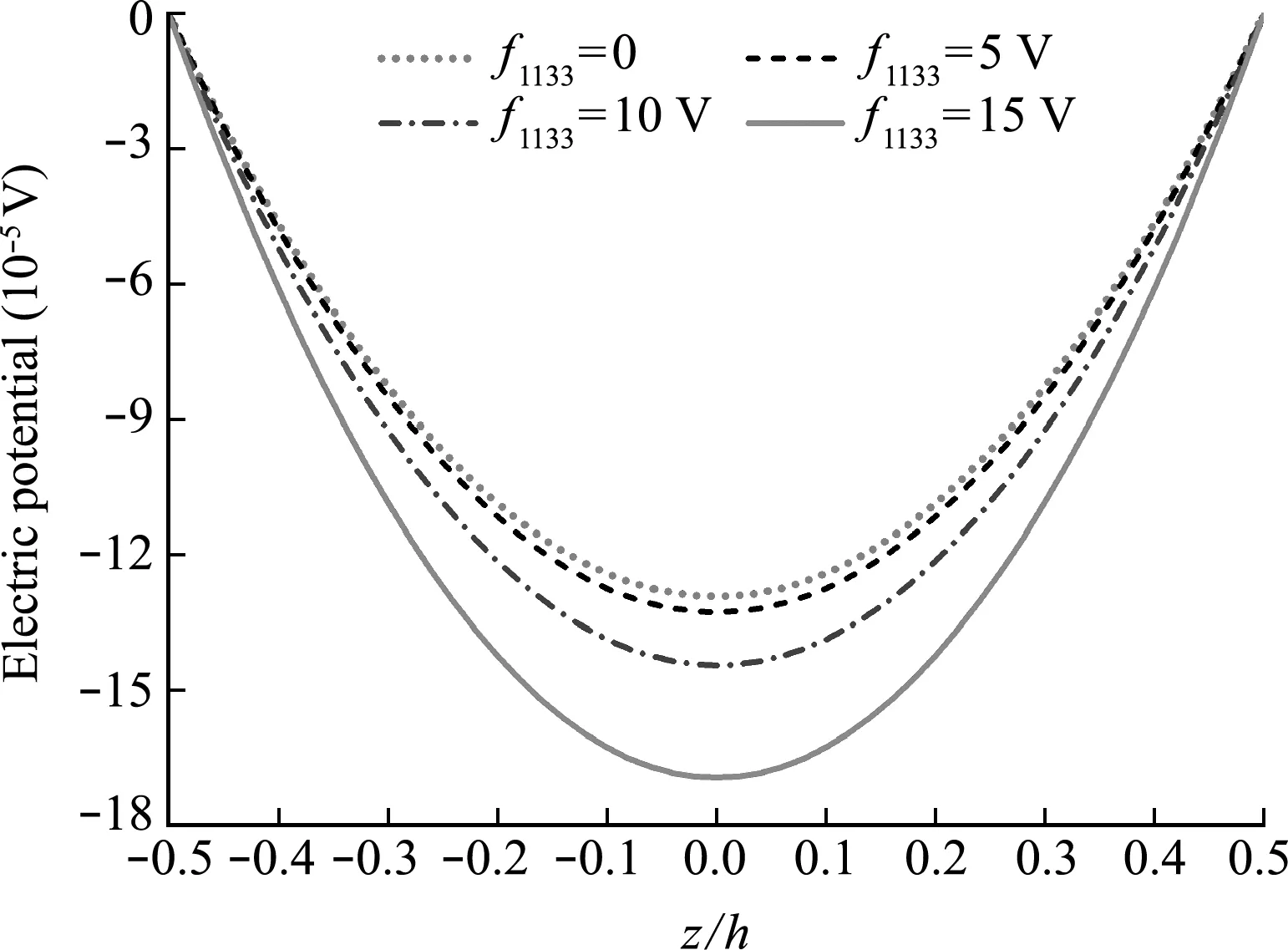
从图1可以看出,简支梁的模型和载荷关于x=L/2对称,故可取梁的一半(0

(5)

(6)

式中I和A分别为梁的极惯性矩和横截面积。

考虑到电极化和电势只存在于z方向,并结合式(5)的后两个式子以及式(6)的最后一个边界条件,可得电极化和电势的表达式为

(7)

(8)

将式(7)代入式(5)的第一个式子,可得压电纳米简支梁的挠度控制方程以及在x=0和x=L/2处的边界条件

(9)

(10)

(11)

由挠度控制方程及边界条件求解得到挠度的表达式为

w=C1+C2x+C3x2+C4x3+C5eS0x+C6e-S0x

(12)

式中

(13)

令控制方程(9)和边界条件(10)有关电学的项为0,即令f1133=f1113=0,d311=0,ΔV=0,再令λ1=2,λ3=2,λ5=1,便可以得到基于Lam等[22]的应变梯度理论的简支梁挠度表达式

(14)

4 纳米欧拉梁的有限元模型

基于有限单元法理论,建立纳米欧拉梁的有限元模型以研究纳米梁的力电耦合特性。首先根据有限元理论,将简支梁的控制方程(9)变换为弱形式方程

(15)

式中M*=-[f1133ΔV/(a33h)]A相当于作用在梁两端的等效弯矩。

由式(15)可以看出,弱形式方程包含w的三阶导数,因此,本文将欧拉纳米梁离散成两节点六自由度,满足C2弱连续的新欧拉梁单元,该单元包含三个独立的材料尺度参数,可以表征尺寸效应。

欧拉纳米梁的挠度w可以由一组含有待定参数的试函数表示为

w=Na

(16)

N1=1-10(x/L)3+15(x/L)4-6(x/L)5

N2=[x/L-6(x/L)3+8(x/L)4-3(x/L)5]L

N4=10(x/L)3-15(x/L)4+6(x/L)5

N5=[-4(x/L)3+7(x/L)4-3(x/L)5]L

(17)

将挠度试函数(16)代入弱形式方程(15),就可以得到新的纳米欧拉梁单元的单元刚度矩阵Ke,

(18)

式中le为每个单元的长度。

集合单元刚度矩阵Ke形成结构的总体刚度矩阵K,最终得到有限元的求解方程

Kw=F

(19)

式中K，F和w分别为整体刚度矩阵、整体载荷向量和整体位移向量。

由式(18)可知,不同于传统的欧拉梁单元,新的欧拉梁单元包含3个独立的材料尺度参数,因此它可以表征尺寸效应。并且,传统的欧拉梁单元只满足C0连续,而新的欧拉梁单元可以满足C1连续和C2弱连续。

5 算例分析

5.1 参数设置

以纳米欧拉简支梁为例,分析和讨论其挠曲电响应。所选材料为BaTiO3。梁的几何形状设定为L=20h和b=3h。悬臂梁自由端的集中力为F=3 nN,梁上下表面的外加电压为ΔV=-0.2 V。3个独立的材料尺度参数设定为l0=l1=l2=10 nm。其他详细参数设置列入表1。

5.2 收敛性分析

无量纲化的挠度、转角和弯矩表示如下

(20)

为确保本文研究方法的收敛性,下面利用新的欧拉梁单元进行有限元计算。在x=L/3处的无量纲化的挠度、转角和弯矩的理论计算结果分别为3.279707,5.226900和-29.795157,表2给出了相应的有限元计算结果。可以看出,本文计算方法收敛且收敛速度非常快。再对比理论计算结果和有限元计算结果可以看出,有限元计算结果最大误差为0.09%,说明本有限单元法的计算精度足够高。由表2可知,30个单元已经足以满足本文的精度要求,因此,在本文将采用30个单元进行计算以及结果分析。

5.3 方法验证

为了验证本文有限单元法的精确度,图2给出两种模型的理论与数值结果对比。一种是基于Lam等的应变梯度理论的简支梁模型,式(14)给出了其理论结果。一种是基于全应变梯度理论的简支梁模型,即为不考虑电学相关项(f1133=f1113=0,d311=0,ΔV=0)的本文研究模型。从图2可以看出,数值结果与理论结果相拟合,本文有限单元法具有很高的精度。对比两种模型的数值发现,以往的应变梯度理论模型可能低估了梁的等效刚度。

表1 梁的材料参数和几何尺寸

表2 x =L /3处的无量纲化挠度和转角

5.4 结果讨论

为了方便讨论,在接下来的结果分析中将给出4种模型。(1) SF模型，同时考虑挠曲电效应和应变梯度弹性项,此为当前的研究模型;(2) FL模型，只考虑挠曲电效应;(3) SG模型，只考虑应变梯度弹性项。(4)NF模型：既不考虑挠曲电效应,也不考虑应变梯度弹性项。

图3为四种模型的挠度曲线。首先对比FL，SG和NF模型的挠度值,可以看出挠曲电效应可以明显地增大梁的挠度,即考虑挠曲电效应后梁的等效弯曲刚度减小,而考虑应变梯度弹性项后,梁的挠度减小,即梁的等效刚度增加。在当前结构尺寸设定下,挠曲电效应和应变梯度弹性项对梁的变形的影响是相反的。这一点可以从梁的等效弯曲刚度k2看出,挠曲电效应会减小梁的等效弯曲刚度,而应变梯度弹性项则会增大梁的等效弯曲刚度。同时,因为挠曲电效应,外加电压相当于在梁的两端施加了等效弯矩M*,这相当于增加了外加载荷,从而使梁的挠度增大。再来看SF模型,相比挠曲电效应和应变梯度弹性项皆不考虑的NF模型,SF模型梁的挠度有所增大,但挠度值还是小于FL模型,这说明应变梯度弹性项对挠曲电效应存在一定的抑制效果,但在当前模型尺寸下挠曲电效应还是起主导作用的。最后,图3的数值结果与理论结果拟合良好,再次验证了本文有限单元法的有效性。

图2 两种模型的理论与数值结果对比

图3 四种模型的简支梁的挠度

令简支梁的材料参数不变,几何尺寸和外加集中力F进行等比例缩放,计算可得四种模型归一化的最大挠度,如图4所示。wN F为NF模型下梁的最大挠度。可以看出,SF模型归一化的最大挠度值随着结构尺寸的减小先增大后减小,存在极值点。而FL模型和SG模型归一化的最大挠度值则分别随着结构尺寸的减小单调递增和单调递减。对于传统的NF模型,随着尺寸的减小,其归一化的最大挠度值不变。从图4可以看出与图3一致的结论,即考虑挠曲电效应之后,梁的挠度会增大,而考虑应变梯度弹性项后,梁的挠度会减小。同时图4还可以看出，挠曲电效应和应变梯度效应都存在尺寸效应,结构尺寸越小,其作用越明显。而对于SF和FL模型,当结构尺寸比较大时,SF模型的归一化的最大挠度值是趋向于FL模型的,说明此时挠曲电效应起主导作用,应变梯度弹性项的作用不明显。随着几何尺寸减小,FL模型的挠度值会迅速增大,而SF模型会出现拐点,说明此时应变梯度弹性项对挠曲电效应的抑制作用增强。当几何尺寸与材料尺度参数相当时,两者的作用几乎相互抵消,所以此时SF模型梁的最大挠度趋近NF模型。

图4 四种模型简支梁的最大归一化挠度

图3～图5为纳米简支梁的力学响应,接下来将讨论其电学响应。图6为外加电压为0,仅有外加集中力作用下时,SF模型在x=L/3处沿厚度方向的电势。由电势的表达式(8)可知,沿梁厚度方向的电势为二次函数,外加电压为0时,梁的上下表面的电势为0,与图6曲线一致。如图6所示,随着挠曲电系数的增大,梁中产生的电势也会随之增大。f1133=5 V时的电势相较于f1133=0时增大了2.6%,f1133=15 V时的电势相较于f1133=10 V时增大了17.4%,这说明挠曲电系数越大,电势增长越快。因此在挠曲电效应的应用中,应当优先选择挠曲电系数大的材料,以保证获得更高的能量转化效率。

最后,图7给出了在只施加集中力时,SF，FL和NF三种模型在不同挠曲电系数情况下的归一化的能量效率deff/dB。能量效率定义为施加在梁上的每单位力载荷产生的电荷量,表示为deff=Q/F,其中Q=∬P(x)dxdy为产生的电荷量,F为外加的集中力。dB=1.05×10-12为NF模型的能量效率。如图7所示,随着梁几何尺寸的减小,FL模型的能量效率持续增高,这验证了挠曲电效应存在尺寸依赖性,而SF模型的能量效率则是先增大后减小,也存在与图4和图5中相似的极值点,这再次说明应变梯度弹性项对挠曲电效应具有抑制作用,并且尺寸越小,其抑制作用越明显。因此,在纳米尺度的研究中,应变梯度弹性项的影响非常显著,不可忽略。当梁的尺寸足够大时,SF和FL模型的能量效率趋于相同。此外,对比不同挠曲电系数的能量效率曲线可以发现,更大的挠曲电系数有助于获得更高的能量效率,与图6的结论一致。

图5 不同电压下SF模型的最大挠度

图6 x =L /3处不同挠曲电系数的电势

图7 不同模型的能量效率

6 结 论

本文基于全应变梯度弹性理论,利用能量法推得了考虑高阶项的纳米欧拉梁的控制方程和边界条件。并且在传统欧拉梁单元的基础上,创建了一种新的满足C2弱连续的欧拉纳米梁单元。这种新的梁单元包含三个独立的材料尺度参数,有2个节点,6个自由度。而后,从新的欧拉梁控制方程出发,根据有限元理论推得弱形式方程,继而推得梁的刚度方程。最后,用有限单元法求解本文算例简支梁的力电响应。通过分析挠度、电势和能量效率,得出如下结论。(1) 挠曲电效应和应变梯度弹性都存在尺寸依赖性,尤其是当结构的特征尺寸接近材料尺度参数时,二者的作用效果都将变得非常显著。(2) 外加电压相当于在梁的两端施加等效弯矩,电压的正负决定等效弯矩的方向。(3) 应变梯度弹性项对挠曲电效应以及能量的转化存在一定的抑制作用,因此在挠曲电问题中,其影响不可忽略。