改进的特征线方法及过载对水锤效应影响分析

马 康， 顾振杰， 白长青*，2

(1.西安交通大学 航天航空学院 机械结构强度与振动国家重点实验室，西安 710049； 2.陕西省先进飞行器服役环境与控制重点实验室，西安 710049)

1 引 言

输流管路系统在飞行器燃油系统、环控系统和液压系统中应用十分广泛，其动力学特性对系统的安全可靠运行具有重要影响。管路运行过程中，会由于阀门突然启闭等作用引起水锤效应，使压力产生急剧变化[1]。由于流固耦合作用，管道内压力的剧烈变化易诱发管道冲击振动，甚至导致管道及其附件的损坏[2]。

目前，应用于有压管道水锤的数值分析方法主要包括特征线方法MOC和有限体积法FVM等。其中，有限体积法FVM可直观地对流体结构和流动机理进行分析[3]，文献[4]基于UDF方法对阀门变速关闭过程的水锤压力进行了计算研究，席志德等[5]利用CFX软件对空间管路的水锤效应进行了数值模拟，Nikpour等[6]基于实验模型对管路水锤进行了CFD仿真，并对不同湍流模型的影响进行了比较分析。但是，该方法需要占用较多的计算资源和较长的模拟时间，对于输流管路系统设计而言效率较低[7]。

MOC方法能够将水锤偏微分方程转换为常微分形式，对整个流体系统进行快速水锤效应分析[8]，可以精确模拟水锤最大和最小压力值，获取水锤发生瞬间的极端参数(压力和流速变化等)，计算精度较高[9]。该方法针对系统各节点建立相应低维非线性代数方程组，能对各种边界条件进行处理，并且只需较少的计算存储容量，计算效率高[10]。20世纪60年代，随计算机模拟技术的快速发展，MOC法已经广泛应用于水锤工程问题。Wylie等[11]在有限差分法基础上发展了MOC法，证明了瞬态流动中MOC法可以较好地反映水锤波的传播及衰减特性。然而，飞行器管路系统还需要面临加速、减速及急速转弯等机动过载的情况。目前，特征线方法对过载作用下水锤效应的分析具有局限性，且其影响机理尚不明确。

基于此，本文在引入过载效应和动态摩阻项的基础上，提出改进的特征线方法，并分析过载作用对水锤效应的影响机理。

2 改进的特征线方法

根据瞬变流基本微分方程，当水平管受到沿管的轴向过载aX和垂直于管轴向的横向过载aY时，推导得到过载作用下的水锤方程表达式。

运动方程：

(1)

连续方程：

(2)

式中H和V分别为测压管水头和平均流速，A，g，τ和D分别为水锤波速、重力加速度、管壁剪切应力和管径。

考虑动态摩阻项的影响，壁面剪切应力为拟稳态摩阻τw s和非恒定项摩阻τw u[12,13]，即

(3)

式中f为Dancy-Weisbach摩阻系数，k为Brunone摩阻系数。

考虑动态摩阻，推导得到修正的水锤波速为

(4)

引入动态摩阻，得到过载作用下水锤方程，

(5)

(g+aY)(∂H/∂t)+a2(∂V/∂x)=0

(6)

根据式(5，6)求解出相应的特征值，

(7)

由式(7)可得改进的常微分方程形式为

(8)

(9)

式中g′=(g+aY)。

对恒定摩阻项进行ε近似求解[14]，化简如下，

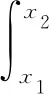
(10)

在特征线C+和C-上进行差分，网格如图1所示，其中C+和C-为2条特征线。

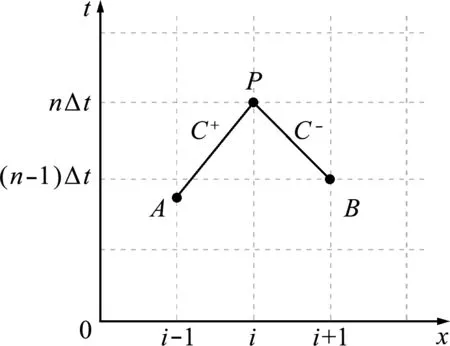
图1 特征线网格

有限差分方程为

(11)

(12)

令B=a/g′，R1=fΔx/(2g′D)，R2=aXΔx/g′。

相容方程为

(13)

(14)

式中

下标i为节点的位置，上标n为计算时间。

边界条件的设置和管道入口处于恒压水头分别如下，

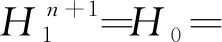
(15)

出口端为阀门，定常流动时阀门孔口的压力降ΔH0与流量[15]的关系为

(16)

式中Cd为阀门的流量系数，AG为流通面积，ΔH为瞬态阀门引起的水头损失。

定义阀门的无量纲开度为

τ=CdAG/(CdAG)0

(17)

联立式(13)，令CV=(V0τ)2/(2ΔH0)，流速为

(18)

根据特征线理论，阀门节点的压力水头为

(19)

3 改进的特征线方法验证

选取文献[16]的水锤效应实验系统作为算例，验证本文提出的改进特征线方法，该系统相关参数列入表1。取阀前管路L1=5880 mm，阀后管L2=170 mm，DN32球阀为计算域，对流场划分网格，在阀芯及连接管道进行网格加密，同时进行了网格无关性验证，如图2所示。网格总数约为894150，最小网格单元尺寸为0.52 mm，网格满足计算要求且合理。

数值模拟采用Realizablek-ε湍流模型求解，管道进口为压力入口，总压恒为12500 Pa，管道出口设置压力出口，静压为3000 Pa。利用滑移网格及UDF控制阀芯转动，修改材料属性及过载动量源项，以1 g过载为例，CFD速度云图如图3所示。

有无过载时，改进的特征线方法计算结果与CFD数值仿真结果的最大压力峰值列入表2，相应的压力波动对比如图3所示，其中也给出了无过载时文献[16]的实验数据。

由表2可知，无过载时改进MOC的最大压力峰值为61.41 kPa，与CFD和实验数据的相对误差为 4.42% 和7.28%；管横向和轴向1g过载作用下改进MOC的最大压力峰值为97.52 kPa和208.21 kPa，与数值模拟的相对误差为5.35%和3.85%；当过载量Δg继续增加至2g和3g时，改进MOC水锤峰值计算结果与数值模拟结果的相对误差在7.7%以内，计算精度较高。

表1 实验系统相关参数

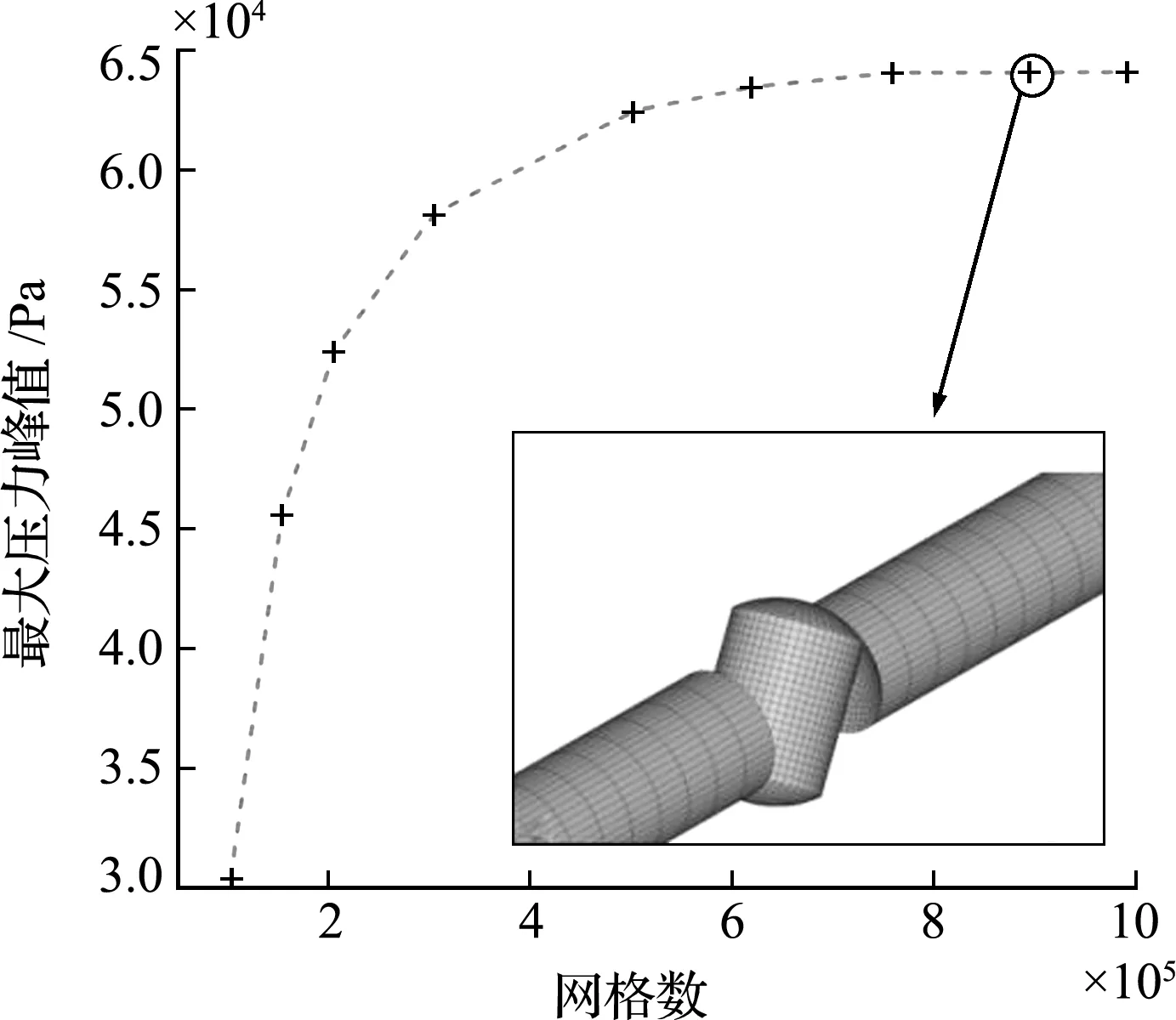
图2 流场网格及无关性验证

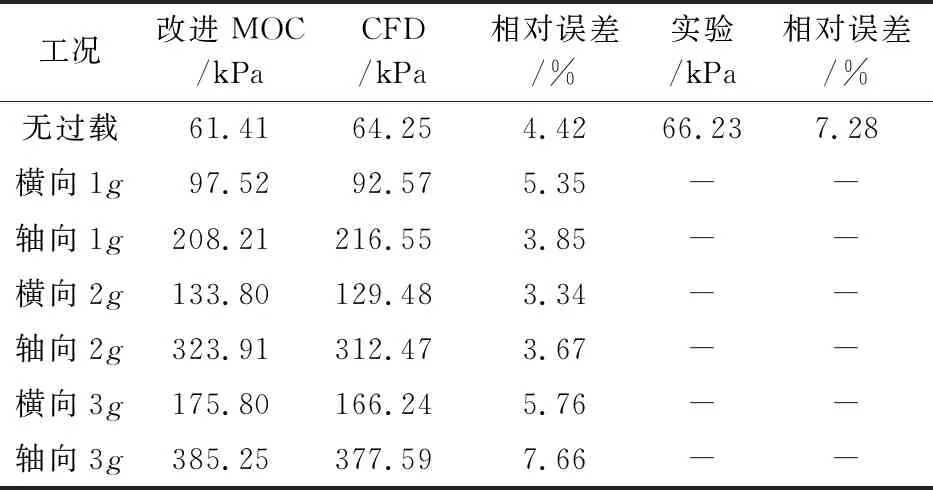
表2 不同过载量下最大压力峰值对比

从图4可以看出，改进MOC和CFD及实测值在无过载时，压力峰值和衰减特性均一致；在不同横向和轴向过载下，改进MOC与CFD结果吻合较好。

4 水锤效应的影响因素分析

4.1 过载量对水锤效应的影响

在恒定过载量作用下，管横向和轴向过载下的具体各周期压力峰值变化的相对系数定量分析列入表3和表4，水锤压力波动对比如图5所示。

图3 最大压力峰值时刻阀门附近的流速(单位：m/s)

pressure peak(unit:m/s)

图4 不同模型下阀门位置压力对比

different models

由表3、表4及图5定量分析可知，恒定过载下，管横向过载对水锤压力的影响小于轴向过载。横向过载量Δg为1g，2g和3g时，阀门位置的水锤最大压力峰值分别为97.52 kPa，133.8 kPa和175.8 kPa；压力峰值的相对系数为1.47，2.02和2.65。而轴向过载量Δg为1g，2g和3g时，最大压力峰值分别为208.2 kPa，323.9 kPa和385.3kPa；压力峰值的相对系数为3.14，4.89和5.82。水锤压力峰值的相对系数在第1和第2周期先增大，在第3～第5周期之后保持基本恒定。

表3 横向过载下各周期压力峰值及相对系数

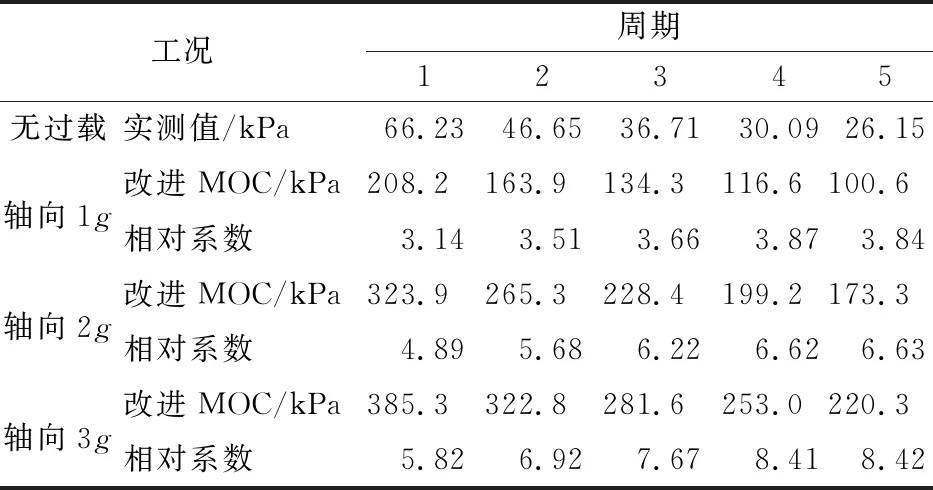
表4 轴向过载下各周期压力峰值及相对系数

图5 不同过载量下水锤压力波动对比

当瞬时过载作用在关闭球阀过程时，以过载量Δg=1g为例，计算管横向和轴向过载下各周期压力峰值及相对误差，结果列入表5，瞬时过载对水锤压力峰值的影响如图6所示。

由表5及图6定量分析可知，作用在关阀过程的瞬时过载对第1周期的水锤压力峰值影响显著，而对第2周期之后的水锤波传播和衰减的影响较小。管横向1g过载下，第1周期的水锤压力峰值为92.16 kPa，第2～第5周期压力峰值与实测值的相对误差保持在7.6%以内；管轴向1g过载下，第1周期的水锤压力峰值为172.41 kPa，第2～ 第5 周期压力峰值的相对误差保持在6.7%以内。

4.2 关阀特性、流体密度和管径对水锤效应的影响

关阀特性主要以关阀时间的变化为例，不同关阀时间下，阀门位置的最大压力峰值随过载量的关系如图7所示，流体密度的影响如图8所示。可以看出，当关阀时间增加时，水锤最大压力峰值减小，过载量Δg越大，峰值减小越显著，压力峰值的变化随密度变化呈正相关性；同时，压力峰值随管径变化呈负相关。

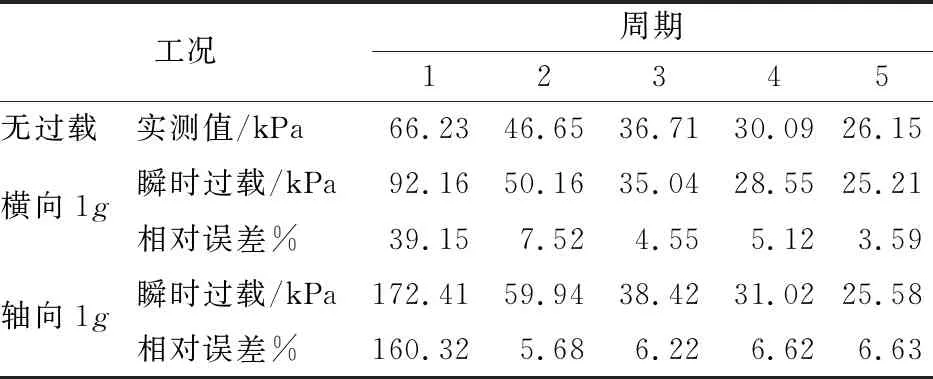
表5 瞬时过载下各周期压力峰值及相对误差

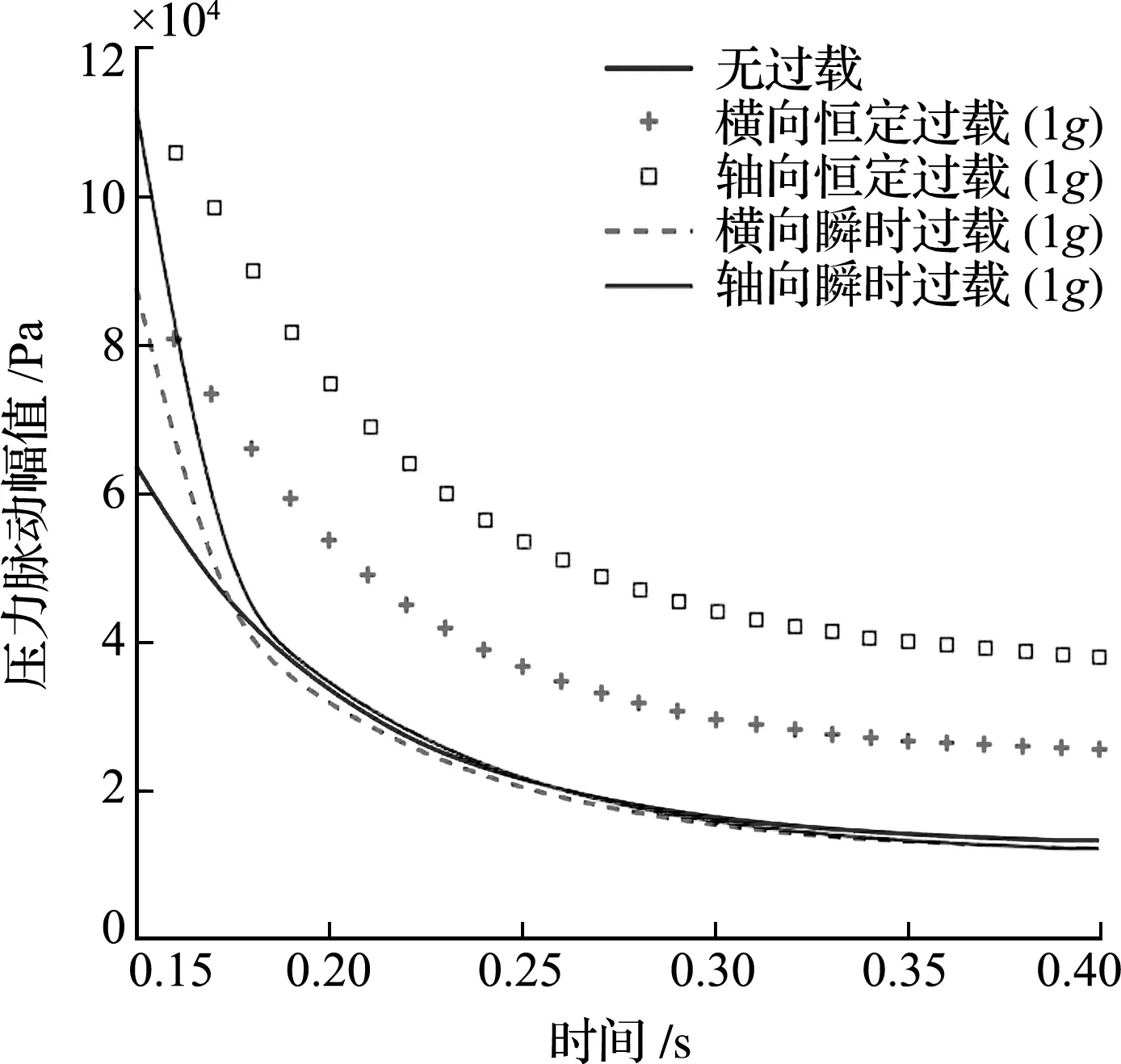
图6 瞬时过载对水锤压力峰值的影响

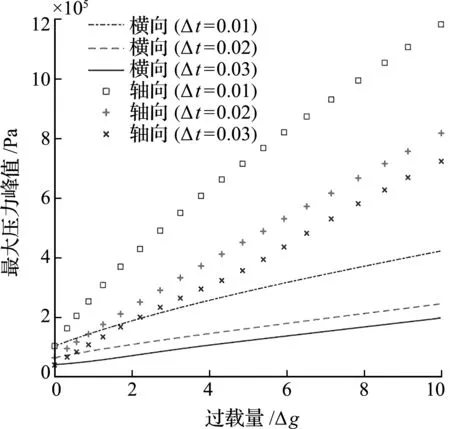
图7 阀门特性对流体压力的影响

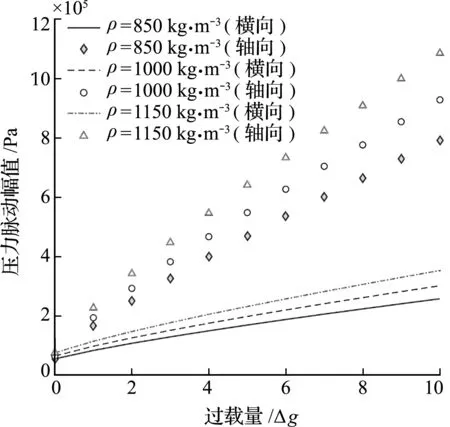
图8 流体密度对流体压力的影响

5 结论

本文在引入过载效应和动态摩阻项的基础上，提出改进特征线方法，给出了改进MOC水锤计算的具体解法，得出以下结论。

(1) 改进MOC在压力峰值和衰减特性上能准确地与CFD数值模拟结果吻合，表明该方法能精确地模拟水锤波动过程，并有效应用于飞行器管路在管横向和轴向过载作用下的水锤计算。

(2) 在恒定过载时，阀门位置的最大压力峰值随过载量的增加而增大，且管横向过载的影响小于轴向过载，最大压力峰值的相对系数在第1和第2周期增大，在第3～第5周期及之后保持基本恒定。

(3) 作用在关阀过程的瞬时过载对第1周期的水锤压力峰值影响显著，而对第2～第4周期及之后的水锤波传播和衰减的影响较小。

(4) 从图7和图8可以看出，当关阀时间增加时，水锤最大压力峰值减小，过载量Δg越大，峰值减小越显著，压力峰值的变化随密度变化呈正相关；同时，压力峰值随管径变化呈负相关。