基于三维接触有限元分析的管片等效抗弯刚度和错台研究
冉春江, 付 强, 杨海天
(大连理工大学 工程力学系,工业装备结构分析国家重点实验室,大连 116024)
1 引 言
盾构法是目前穿越江海大型隧道建设的主要施工方法[1]。作为盾构隧道的主要承力结构,管片衬砌的力学行为直接影响着整个隧道的安全与使用[2]。管片接头部分是盾构管片衬砌环的薄弱部位,其受力/变形状态是设计中必须计及的重要因素之一[3],其相关研究一直受工程界和学者们关注[4-9]。
越江海隧道防水设计尤为重要,防水失效可引起隧道渗漏和隧道不均匀沉降,影响到隧道结构的安全及运营。大量工程实践表明[10],盾构隧道的渗漏主要发生在管片接缝处,而接头张开与错台[11]是导致接缝防水性能下降的重要因素[12]。相关研究表明[11,13],当接头张开量大于6 mm,或者接头错台量大于8 mm时,接头抗渗性能会受到较大影响。此外,管片错台可导致错台处内力显著增加,李宇杰等[11]对已有10 mm纵缝错台管片进行三维有限元分析,得到管片错台轴力最大增加幅度为281%,弯矩最大增加幅度为275%。
本文从两方面对接头张开与错台开展研究。
(1) 管片结构计算中常采用梁-弹簧模型,其在接头处以旋转弹簧模型来等效接头对管片抗弯刚度的削弱作用[4],但弹簧等效抗弯刚度的取值一般很难确定[14],不仅与管片和接头处螺栓以及衬垫部件的几何尺寸、材料性质、接头的构造形式和螺栓预紧力等因素有关,还与接头处的内力存在非线性关系[4,5,15-17]。这些因素不仅增加了相关实验研究的经济与时间成本,也使得目前各种接头刚度的理论分析模型和经验公式都难免有一定的局限性[1]。本文利用高精度有限元数值解模拟实验结果,借助基于挠度等效的反问题求解,提出了一种确定管片接头等效抗弯刚度的新方法。另一方面,利用不同轴力-弯矩组合下反演的结果,建立了基于Kriging代理模型的轴力-弯矩-等效抗弯刚度的非线性关系,提出了由此关联的管片结构非线性问题的数值求解方法。
(2) 李宇杰等[11]指出,通过有限元计算得到的错台量较一些现场监测和室内试验结果偏小,这可能是由有限元仿真中施工情况模拟不充分所致。而作为影响管片接头错台重要因素[18]的螺栓孔间隙和橡胶衬垫变形,在已有的数值模型[9,11,19-25]中考虑不够充分,文献[19-21]直接将螺栓简化为梁单元,将橡胶衬垫简化为法向弹簧单元处理,文献[9]则将衬垫作为垫片单元处理,文献[11,22-25]虽然将螺栓和衬垫考虑为三维实体单元,但并没有考虑螺栓孔间隙和衬垫变形对接头错台的影响。为此本文建立了考虑螺栓/螺栓孔间隙以及橡胶衬垫的三维有限元接触计算模型,通过数值分析,着力探讨了螺栓间隙及衬垫对管片接头错台的影响。
2 管片接头等效抗弯刚度的反演模型
本文基于目前模型实验和数值仿真中常采用的直管片-接头模型[4,9,15,26-28]进行研究,如图1所示。管片一端为固定铰支座,另一端为可水平移动的铰支座,两端施加轴向荷载N,在距两端a=L/2处施加竖向荷载P。
在梁-弹簧模型中,接头处的等效抗弯刚度kθ定义为在给定轴向压力作用下,相邻管片在接头处产生单位相对转角所需要的弯矩[4]。
kθ=M/θ
(1)
目前,接头等效刚度的确定主要有两类方法,(1) 通过试验或三维有限元数值仿真,获取如图2所示的接缝转角,或通过张开量计算相应的转角,再利用式(1)计算等效抗弯刚度[4,9,27,28]; (2) 通过假定管片接缝处的受力形态[14,25,29-33]或将管片接头面的相关部分简化为弹簧和刚性板或梁等结构[8,34-36],利用接头处的平衡和变形协调关系[5]导出弯矩-转角的关系,从而得到管片接头抗弯刚度的显式或隐式表达。
以上处理方法的优点是物理意义明确,便于直接操作,但利用信息比较局部。另一方面,由于接头处的情况比较复杂,如何将这些信息有效地等效为与梁-弹簧模型相适应的转角是一个值得进一步深入探讨的问题。
准确预测等效刚度的最主要目的,是为了使梁-弹簧等效模型更有效地等效三维管片-接头问
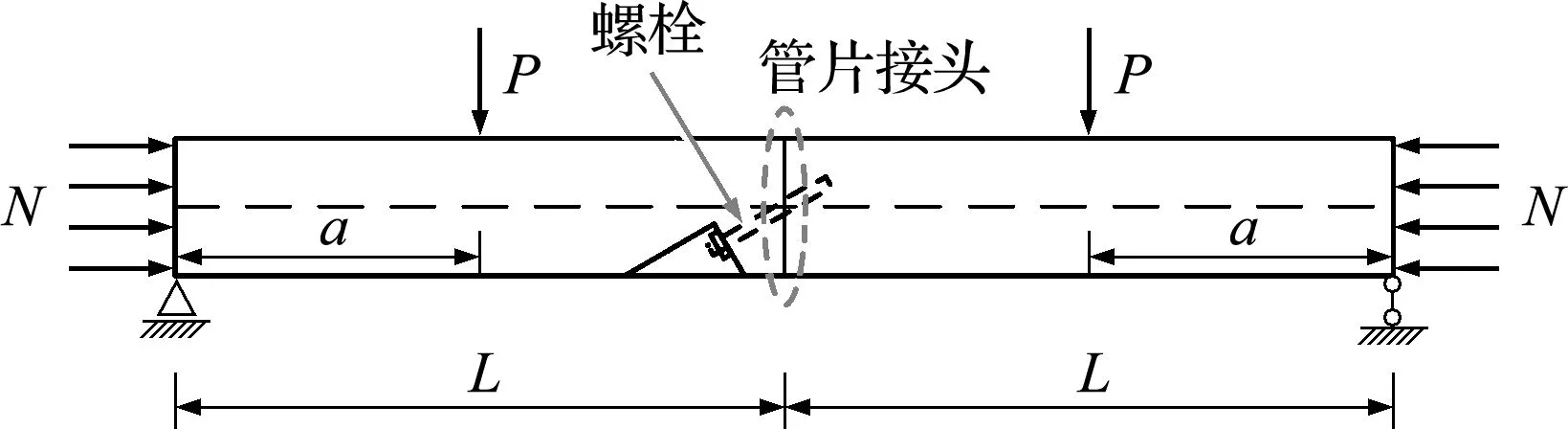
图1 管片接头受载示意图
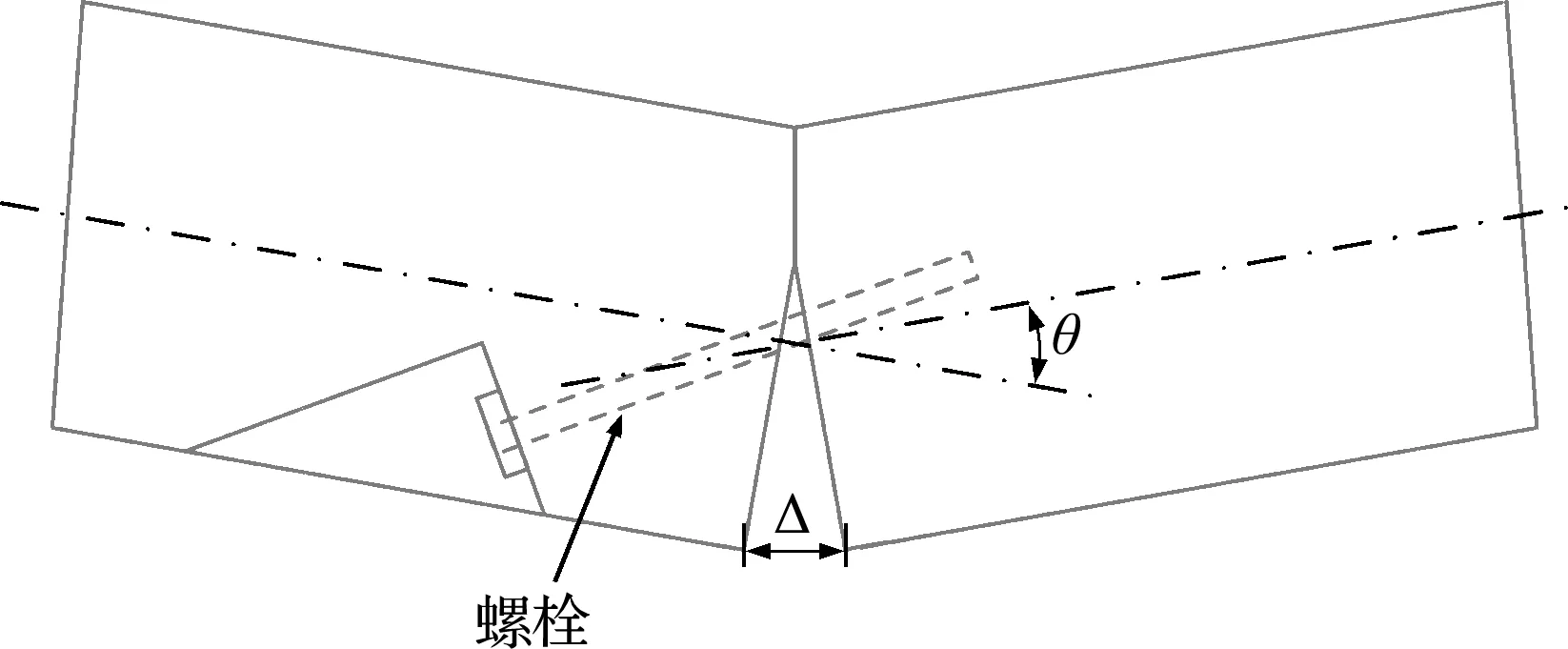
图2 管片接头变形示意图
题的变形和受力分析。为此,本文基于三维管片-接头模型与梁-弹簧模型的整体挠度等效,建立了一个确定等效抗弯刚度的反问题求解方法。
将图1所示模型按梁模型等效,管片在接头处位移(挠度)连续,接头处的转角-弯矩关系为M=PL/2=kθθ(本文限于θ为有限值),由此可得梁的挠度曲线方程为
(2)
式中x为梁的轴向坐标,θ是未知的并与载荷相关的相对转角。
若将三维管片-接头有限元分析获取的位移,作为参数θ未知的梁弹簧模型的挠度测量信息,则θ的确定可以看作一个参数辨识反问题,并可通过下列以式(2)为约束条件的优化问题求解。
(3)
式中wθ(x,θ)由式(2)给出,w*由三维管片-接头有限元分析给出。
本文利用ANSYS对图1的结构进行三维接触有限元分析,将其相关结果作为等效梁弹簧模型的纵向挠度,利用MATLAB软件中的fminsearch函数实现式(3)的极小化。θ值确定后,由式(1)计算相应的kθ作为管片接头的等效抗弯刚度。
3 管片接头的三维接触有限元模型
图3为直管片接头的三维有限元模型,单个直管片的长度为4 m,宽为2 m,厚度为0.7 m。管片主体部分选用8节点空间六面体单元,螺栓孔和手孔附近采用4节点四面体单元,六面体单元和四面体单元连接处采用5节点五面体单元过度;管片部分的有限元模型包含64622个单元和38113个节点。两管片间由三颗M36螺栓连接,螺栓有限元模型包含16986个8节点六面体单元,每个螺栓中间添加了PRETS179预紧力单元,并通过SLOAD命令施加了150 kN的预紧力。

图3 管片和螺栓的有限元网格
两管片之间,以及管片与螺栓之间存在接触关系,如图4所示。其中A处采用的是面-面接触单元模拟,用单元高斯积分点来判断接触状态,接触类型为粗糙;不考虑螺栓螺纹的影响,螺栓与管片混凝土在B处考虑为绑定接触;螺栓与螺栓孔壁有2 mm的间隙,在C处螺栓与螺栓孔壁间设置了接触单元以处理可能发生的接触;由于预紧力的存在,螺帽与管片之间不会发生滑移,故D处考虑为绑定接触。
混凝土管片和螺栓考虑为线弹性材料,弹性模量分别为37.5 GPa和210 GPa,泊松比分别为 0.17 和0.30,建模不考虑管片配筋的影响。
为确保数值结果对网格的稳定性,将网格数量加密到原来的两倍后,以轴力10000 kN和偏心距为4000 kNm试算,两种网格下中点位移仅相差 2.61%,表明采用的网格尺寸可以保证数值结果的稳定性。
4 反演结果及接头刚度的Kriging代理模型
利用以上反演模型,对164组载荷组合进行等效抗弯刚度预测。轴力N取10000 kN,20000 kN,30000 kN和40000 kN四组,每组轴力下弯矩M取41组,弯矩=偏心距×轴力,偏心距在-0.4 m~0.4 m 以间隔0.02 m均匀取值。
图5(a)为不同轴力下等效抗弯刚度-偏心距曲线。图5(b)为不同轴力下接头端面张开量随偏心距的变化,张开量为三维有限元模拟所得的两个管片接头端面上的最大张开距离。
从图5可以看出,(1) 等效抗弯刚度是载荷相关的。在相同轴力作用下,当偏心距小于0.18 m时,弯矩的效应很小,整个接缝面几乎都处于受压状态,因此接头端面的张开很小,从而导致接头等>效抗弯刚度变得很大;当偏心距大于0.18 m后,随偏心距的增加,弯矩的效应逐渐增强,接缝面张开也随之增大,从而导致等效抗弯刚度减小。(2) 轴力对等效刚度的反演影响较小,如图5所示,四条曲线虽然轴力变化很大,但反演得到的接头刚度变化却很小,说明等效刚度的变化主要是轴力偏心引起的弯矩所致。
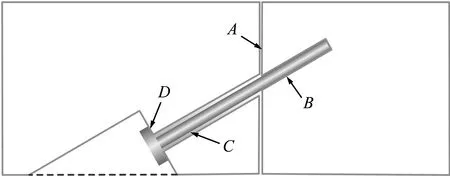
图4 接触面
为建立抗弯刚度与载荷之间关系,本文利用以上164组计算结果作为测量信息,应用DACE工具箱[37]提供的Kriging模型来近似(代理)接头刚度和接头张开量与轴力及偏心距(弯矩)之间的近似非线性关系。Kriging代理模型作为估计方差最小的无偏估计模型,在解决非线性程度较高的问题时较易取得理想的拟合结果[38]。
所建代理模型的性态如图6所示。表1给出了样本点以外的四种载荷组合下反演的等效刚度与代理模型预测值之间的比对,表明Kriging 模型代理可提供精度合用的代理预测。
在后续的计算分析过程中,若给定接头处的轴力和弯矩,可通过代理模型便捷地获取相应的接头抗弯刚度。

图5 不同轴力下等效刚度和接头端面张开量随偏心距变化
5 管片-接头的非线性分析
借助以上建立的Kriging代理模型,可进行基于梁-非线性弹簧模型的管片衬砌结构的计算分析,计算流程如图7所示。
取管片截面厚为0.7 m,宽为2.0 m;管片外径为15.5 m,内径为14.1 m,计算模型包含一环管片衬砌,由十片管片构成;管片材料为C70混凝土,弹性模量取37 GPa,泊松比取0.17,密度取2300 kg/m3;载荷采用水土合算,水深为80 m,埋深为40 m;土层容重为19600 N/m3;侧压力系数为0.65,土层抗力系数取5000 kN/m3;螺栓预紧力设为150 kN。所建代理模型包含了算例中轴力和偏心距的变化范围。
三维管片-螺栓-接触有限元计算所得管片位移云图如图8所示。可以看出,管片环变形最大的地方在衬砌底部和顶部,其次是衬砌的两侧,变形最小的地方在衬砌的上下左右45°位置,整个衬砌变形后呈上下压扁的椭圆形状。
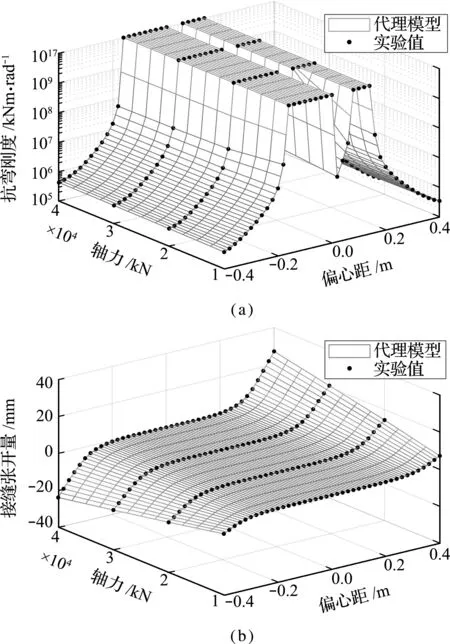
图6 代理模型性态

表1 等效抗弯刚度比较
图9~图12分别是梁-非线性弹簧模型计算得到的管片轴力、弯矩、剪力和位移与三维有限元计算结果的对比,表2是轴力、弯矩、剪力和位移结果的最大偏差。三维有限元分析的内力计算结果,由相关截面上的应力通过数值积分得到。
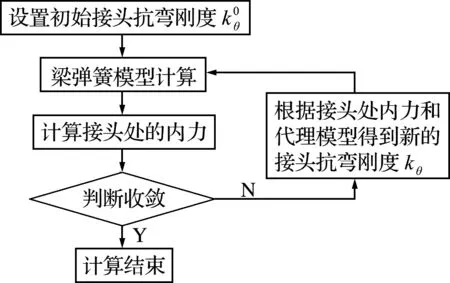
图7 迭代计算流程
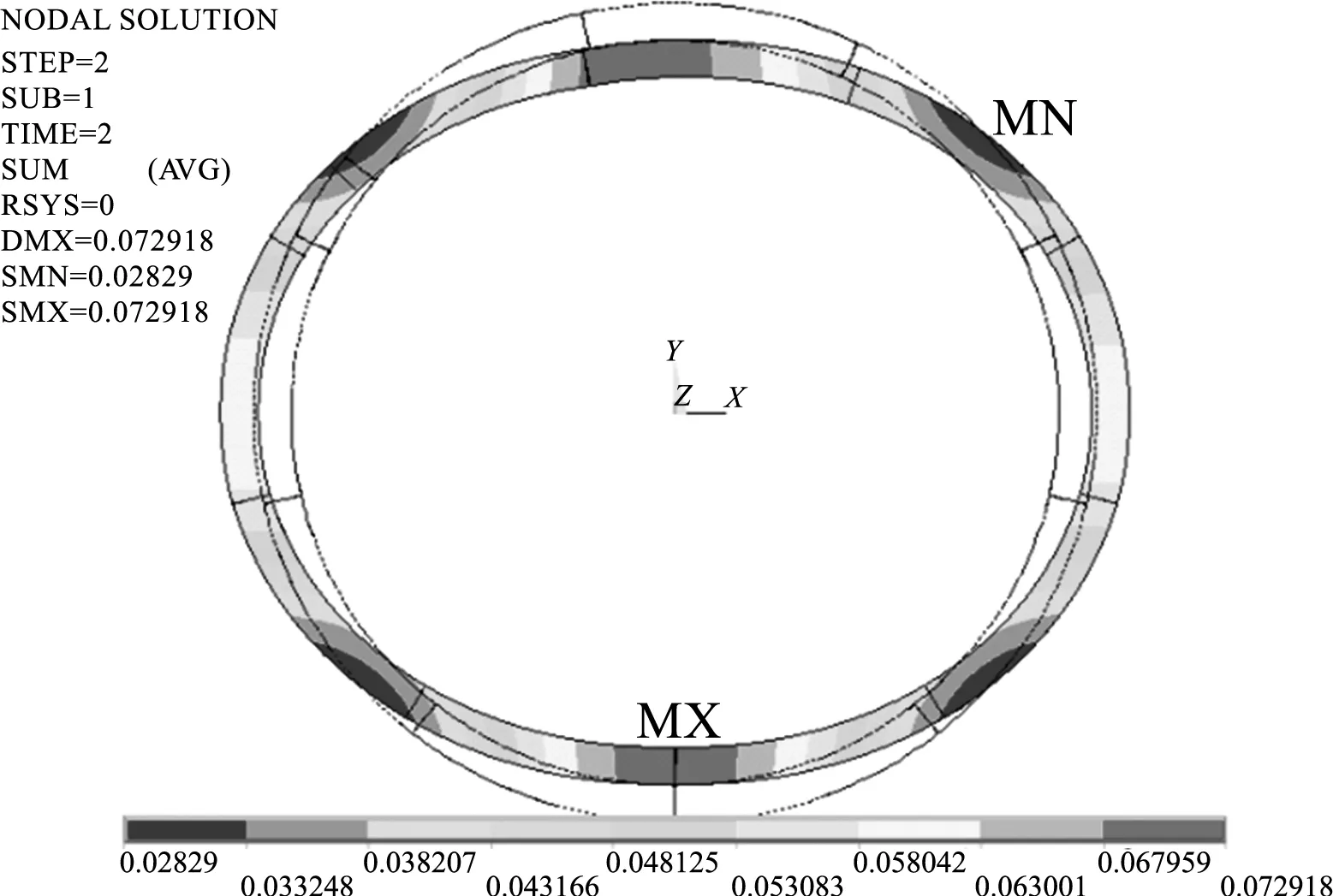
图8 管片变形云图(放大系数:10)

图9 轴力结果对比

图10 弯矩结果对比
结果表明,梁-非线性等效弹簧模型所计算的内力和变形与三维管片接触有限元模型的计算结果基本一致,等效效果良好。在0°,90°,180°和270°个别位置处两者偏差较大,一方面是用一维模型来近似三维模型会有一定的误差,虽然用非线性接头弹簧考虑了接头对管片刚度的削弱作用,但并不能完全考虑手孔和螺栓孔等部件的影响;另外,三维结构的内力是由相关截面上的应力通过数值积分等效的,会产生数值误差。
6 基于三维接触有限元计算的管片错台分析
6.1 三维数值计算模型
参照原型实验[39],管片尺寸取为667 mm×700 mm×2000 mm,管片两端约束条件为简支,采用1/3幅宽进行数值模拟。以顺剪的形式加载,如图13所示。轴力N取2000 kN,剪力Q取2000 kN,斜螺栓预紧力取100 MPa。
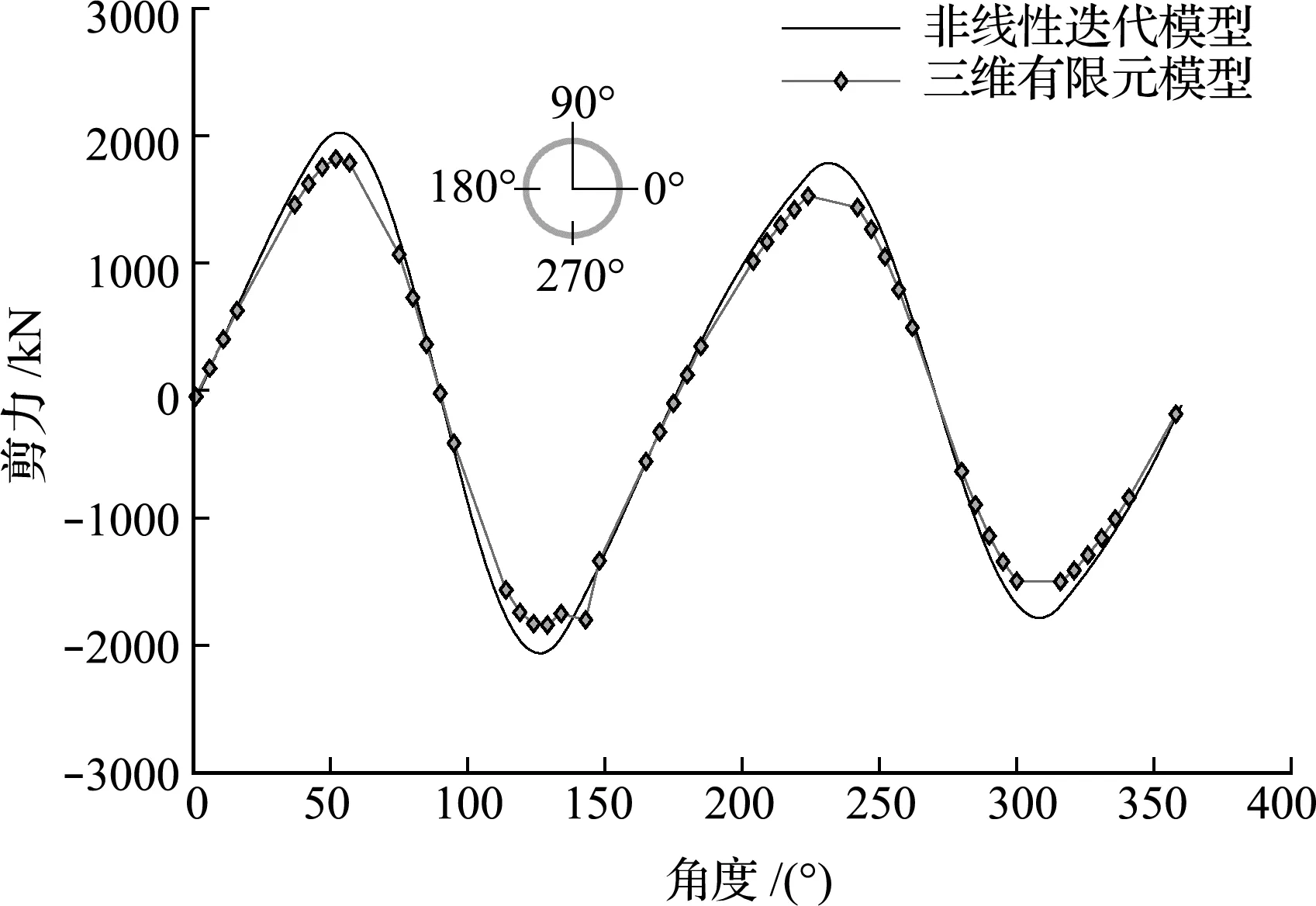
图11 剪力结果对比

图12 位移结果对比

表2 两种算法计算结果最大偏差对比
斜螺栓采用M30螺栓,考虑到螺栓与螺栓孔之间存在间隙,根据《盾构隧道管片设计》[40],M30螺栓孔直径可取范围为35 mm~38 mm,本文取36 mm,衬垫厚度取3 mm。
螺栓侧面分为含螺纹部分与不含螺纹的光滑部分,如图14所示。含螺纹部分与管片接触采用绑定连接,不含螺纹的光滑部分采用法向硬接触和切向光滑的接触模式。管片与衬垫之间采用法向硬接触和切向摩擦的接触模式。
计算模型中包含管片、螺栓和衬垫,均采用三维实体单元。管片和衬垫采用四节点线性四面体单元(C3D4),斜螺栓采用八节点线性六面体单元,非协调模式(C3D8I),有限元模型如图15所示,其中管片和螺栓包含150628个单元,超弹性的衬垫则由程序自适应加密网格以降低大变形引起的单元畸变。所采用的计算模型通过网格加密验证了有限元网格的独立性。
混凝土与螺栓均采用线弹性材料本构模型,本构参数列入表3。
盾构隧道管片的软木橡胶衬垫以橡胶和软木粉粒为主要原料,其应力应变关系具有较强的非线性特征[42]。本文采用Mooney-Rivlin一阶本构模型[43],如式(4)所示。

图13 加载方式

图14 接头螺栓及管片有限元网格

表3 混凝土与螺栓材料参数
W=C10(I1-3)+C01(I2-3)
(4)
式中I1和I2为变形张量不变量,
(5)
(6)
λ1,λ2和λ3为主伸长比。本文计算中,以三元乙丙橡胶[44-45]为参考,C10=561 kPa,C01=225 kPa。
6.2 计算结果与分析
考虑螺栓与螺栓孔壁之间存在间隙,表4为衬垫材料采用线弹性(弹性模量取150 MPa,泊松比取0.32[24])与超弹性本构模型所得错台量的比较。与线弹性情况相比,衬垫材料为超弹性时的错台量增加幅度为111%。
考虑衬垫为超弹性材料,表5给出螺栓孔间隙对接头错台量的影响,与不考虑情形相比,增加幅度为197%。螺栓孔间隙的存在,使得受载时螺栓与孔壁接触需要一个过程,在此期间螺栓的不完全参与会导致错台量的增加。图15给出了加载过程中接头错台量的变化历程,图16给出了A,B和C三个时刻螺栓与螺栓孔壁间的接触情况,可以看出,接头错台主要发生在A-B和 B -C 阶段,总计达到了 6.78 mm,这两个阶段是螺栓与两边的螺栓孔壁接触的过程;C-D阶段产生的错台量约为2.24 mm,与不考虑螺栓孔间隙时的错台量相当,此时螺栓与螺栓孔壁已经完全接触,这部分错台主要由螺栓、管片和衬垫的变形产生。

表4 衬垫本构模型对错台量的影响

表5 螺栓孔间隙对接头错台的影响

图15 接头错台量变化历程
综上可以看出,螺栓孔间隙和橡胶衬垫本构关系对管片纵缝错台量有着显著影响。
以上计算中的摩擦系数根据文献[41]取0.3,当摩擦系数取为0.4和0.5时,得到的最大错台量分别为8.91 mm和7.62 mm,表明摩擦系数对错台量也有影响,但影响较小。
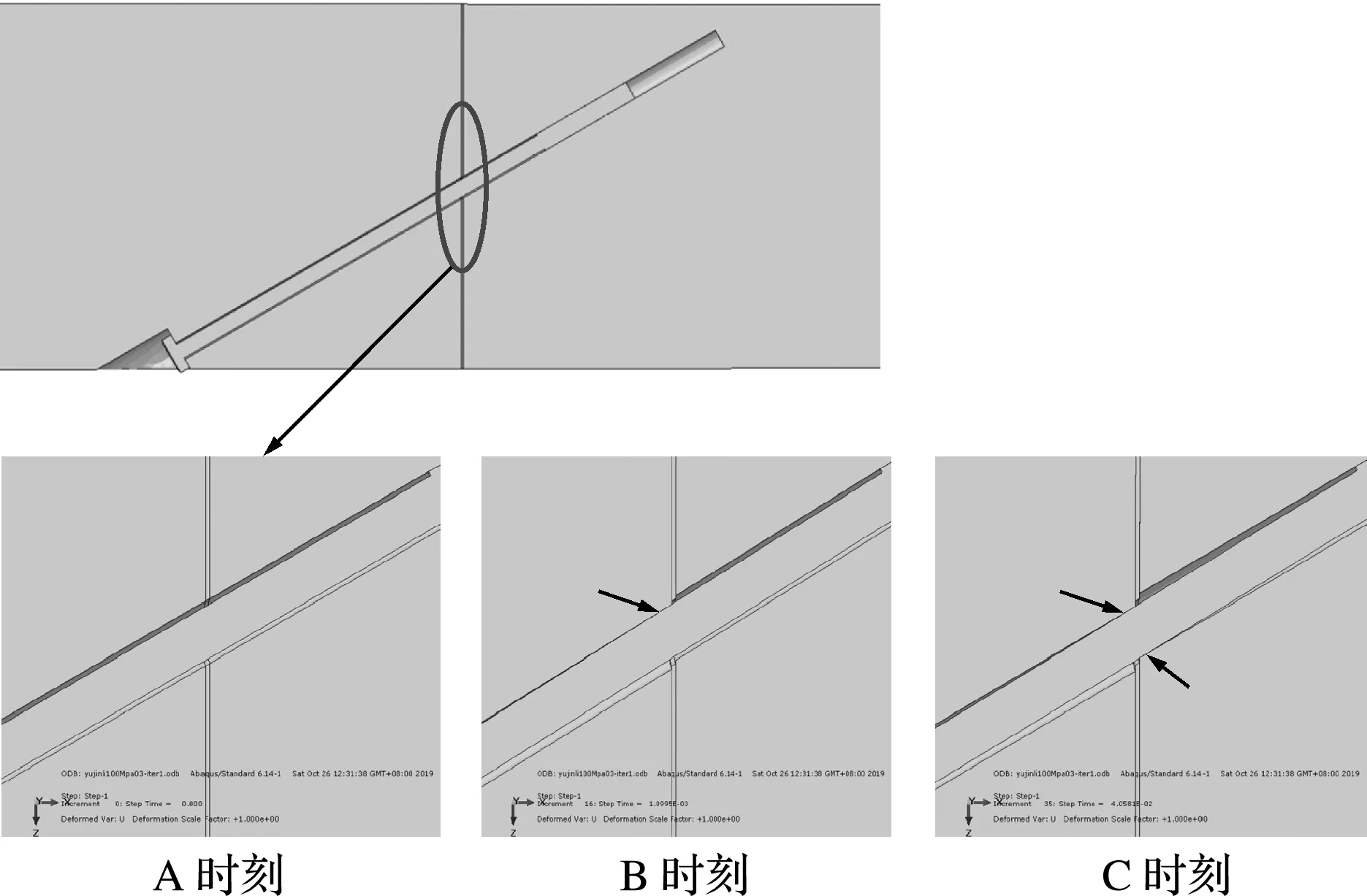
图16 不同加载时刻螺栓接触情况
7 结 论
首先,本文提出了一种以三维接触有限元模拟结果作为测量信息,借助基于挠度等效的反问题求解确定管片接头等效抗弯刚度的方法;利用所提方法,通过不同轴力-偏心距组合下的反演结果,建立基于Kriging代理模型的轴力-弯矩-等效抗弯刚度的非线性关系,并提出了一个由此关联的管片结构非线性问题的数值求解模型。
准确预测等效刚度的主要目的是使梁-弹簧模型更有效地等效三维管片-接头问题的变形和受力行为。因此,从两个模型整体的等效效果出发确定等效抗弯刚度,比利用局部信息更为合理。本文基于这个思路,给出了一种基于整体挠度等效的预测方法。梁-弹簧模型将管片作为梁处理,是为便捷计算的一种近似,为更准确地描述管片的力学特性,还可考虑基于壳模型的等效方法研究。
管片接头等效抗弯刚度是载荷相关的[4,5,15-17],由于实际问题中截面载荷是预先未知的,这种相关性导致了结构分析的非线性。利用基于代理模型的载荷-等效抗弯刚度的非线性关系,可方便地预测不同载荷下接头的等效抗弯刚度,因而可将此非线性关系用于管片衬砌的非线性分析。与三维有限元结果相比,所提管片结构非线性计算模型可较为准确地预测管片结构的内力和变形,表现出良好的整体等效性。
其次,本文建立了考虑螺栓孔间隙和橡胶衬垫超弹性本构的三维有限元接触计算模型,着力探讨了螺栓孔间隙与衬垫本构关系对管片纵向错台量的影响。
就数值结果而言,本文错台量计算值与文献[39]同尺度同载荷无衬垫错台实验结果10 mm很接近。文献[11]在总结一些文献后曾指出,一些有限元模拟计算得到的错台量约为1.5 mm,而现场观测与室内试验的结果约为10 mm。由于研究的具体问题/模型不同,数值结果相近的原因需进一步深入分析。但从本文数值模拟的结果来看,在管片纵缝错台的研究中需充分考虑螺栓孔间隙和衬垫本构模型的影响。

