钢纤维对混凝土轴压性能影响的试验研究

陈升平，倪 亮，卢应发，田 肖

(湖北工业大学土木建筑与环境学院，湖北 武汉 430068)

近年来，随着中国经济的迅猛发展，现代化工程对混凝土提出了更高的要求。显然，脆性大的普通混凝土已经无法满足现代工程的需要。因此，国内外相关学者对纤维增强混凝土这种复合材料的力学性能展开了大量研究[1-6]。其中，钢纤维混凝土成本低，制造方式简易，增韧效果好，应用最广泛。赵顺波[7]通过对0%～1.6%钢纤维掺入率的全轻混凝土进行轴压试验，提出了两类混凝土单轴受压应力-应变曲线统一计算模型及其特征点计算公式。黄彪[8]等人认为:随着钢纤维体积掺量和长径比增加,混凝土峰值应力和峰值应变明显提高,其韧性和延性得到显著改善。Mingshuang Zhao[9]设计了钢纤维体积分数分别为0%、0.4%、0.8%、1.2%、1.6%和2.0% 的钢纤维混凝土。进行单轴压缩试验并得出了应力-应变曲线。结果表明，随着钢纤维体积分数的增加，应力-应变曲线峰值应力处的压应变增大，而应力-应变曲线下降部分的斜率减小。杨克荣[10]试验结果表明:试验机的加载速率与混凝土的抗压强度呈正比，钢纤维对于强度的影响较小，对混凝土的影响主要是使其韧性提高。

在混凝土中掺入一定体积率的钢纤维，可以显著改善混凝土的抗裂能力，改变其破坏形态。因此，这里将通过三个变量的正交试验，分析钢纤维对混凝土轴压力学性能的影响，能为钢纤维在工程中的应用提供参考。

1 试验方案

1.1 试验材料

试验用料分别采用钢丝冷拉和钢板剪切工艺制作而成的剪切型和多锚固点型钢纤维，强度P.O42.5水泥、5～20 mm瓜米石、中粗普通河砂、高效粉末减水剂、城市生活用水等。为了降低粗骨料中的泥灰杂质，瓜米石需要经过冲洗、晾干后使用。钢纤维参数及类型见表1、图1。

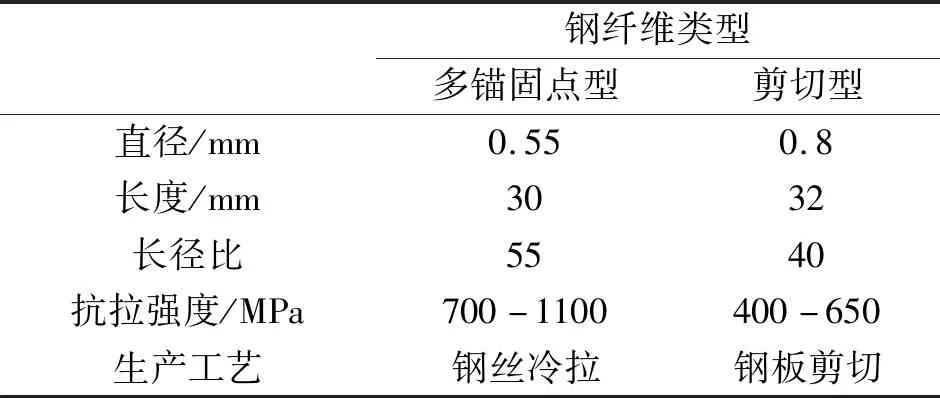
表1 钢纤维参数

图1 钢纤维类型

1.2 试验设计

合计浇筑21组圆柱体及相同数量的立方体试件，每组数量3个，尺寸分别为150 mm×300 mm和150 mm×150 mm×150 mm，其中设置3组普通混凝土作为对比项。以钢纤维掺量及类型为变化量研究对不同强度混凝土的影响，并进行了相对应的正交设计(表2)。X1～X3表示混凝土强度等级，Y1～Y3、Z1～Z2则表示为钢纤维含量及类型。

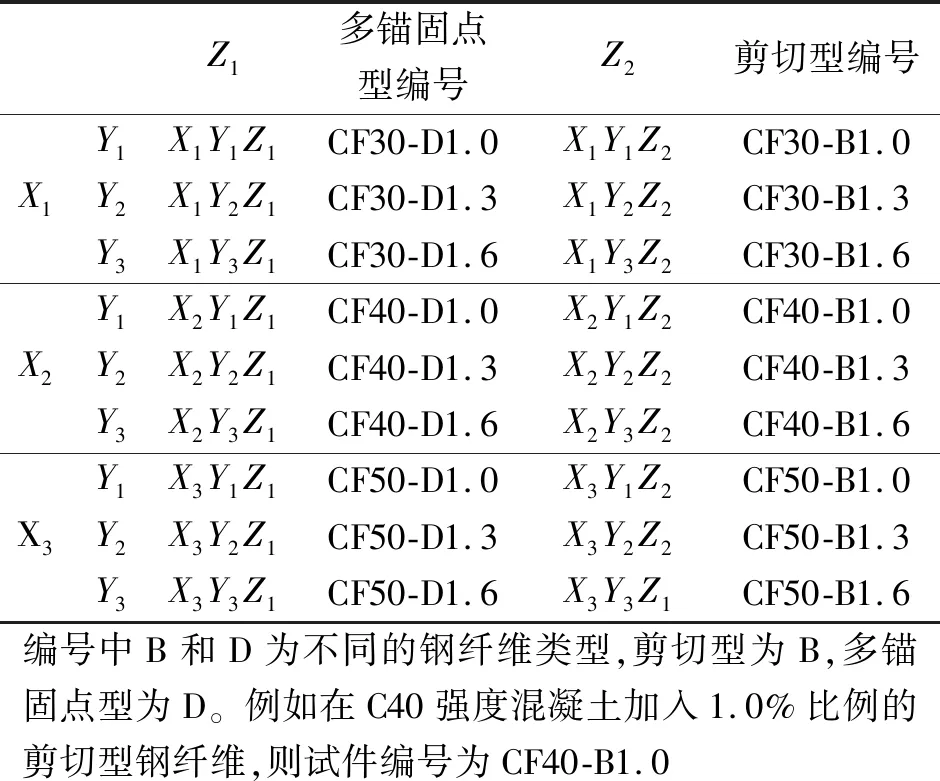
表2 试件的参数及编号

1.3 加载装置

试验加载装置如图2所示，位移控制加载，位移计间距100 mm，轴向位移的测试由位移传感器实现，并在试件的中部对称竖向粘贴两个应变片，并使用应变采集仪DH3816及配套电脑软件进行数据采集。

图2 试验加载装置

2 试验结果与分析

各组试验结果的平均值如表2所示，其中fcu为立方体试件抗压强度，fc为圆柱体轴心抗压强度，ε0为混凝土峰值应变、εcu为混凝土极限压应变，fr为压应变0.01时的残余应力。

2.1 破坏特征

由于使用位移控制加载，位移缓缓提升的过程中，机器传给试件表面的压力不断增大，当压力接近试件的极限抗压能力，试件中部及上下两个表面边缘出现可用肉眼观测的较小裂纹，并不断从两端至中间缓慢延申，而后机器压力达到试件的抗压极限，裂缝宽度逐渐变大，压力机所显示的荷载出现一定程度的降低，而后裂缝延申速度加快，混凝土内部各类材料所共同形成的摩擦力、粘结力及残余抗压能力逐渐降低。该阶段延续的过程中，可听见混凝土碎末因受压剥离外表面、钢纤维被拔出的响声。维持一定时间后，应变采集仪配套电脑上显示的位移突然急剧增加，压力机所显示荷载的快速降低，此时的试件不再具备压缩变形能力，丧失稳定性及残余承载能力。破坏后的试件可观测到贯穿裂缝，倾角约为45°(图3)。得益于钢纤维在混凝土内部的随机分布，不仅抑制了混凝土外表面的剥离，而且还对裂纹宽度及数量有极其显著的限制作用，所以使得试件的完整性得到比较好的保留。

表3 主要试验结果

图3 钢纤维混凝土圆柱体破坏形态

2.2 抗压强度

如图4所示，钢纤维明显增强了C30、C40混凝土立方体试件的抗压强度。如掺入1.6%的多锚固点型钢纤维，使得C30强度普通混凝土抗压强度提高11.3 MPa，增幅达34.84%。

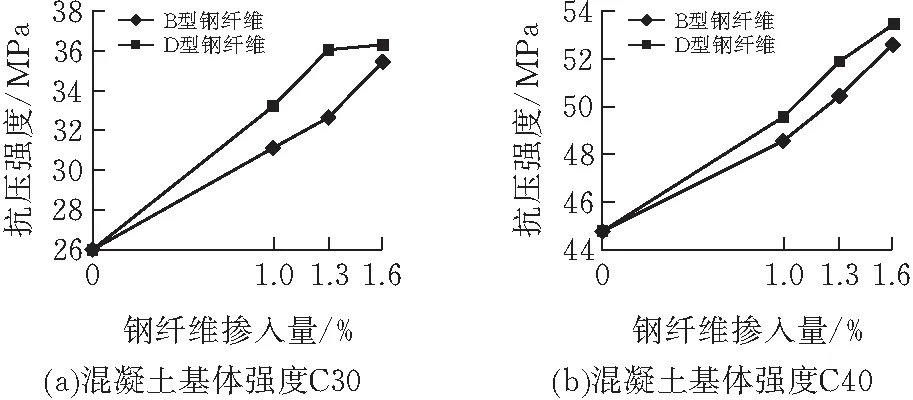
图4 立方体抗压强度变化趋势

对于C50强度混凝土，钢纤维对强度提升的作用并不显著，在钢纤维掺入率1.0%～1.6%情况下，抗压强度增长幅度至多为12.8%，钢纤维对高强度混凝土抗压性能的改善效果没有C30、C40强度时显著。混凝土强度为C50，通过改变剪切型钢纤维的掺量，使其含量从0提升至1.3%，抗压强度呈线性增长，但将其含量从1.3%提升至1.6%，抗压强度降低了0.6 MPa，因此剪切型钢纤维对于抗压强度具有双向作用，可能是增强或减弱。作为对比组，随多锚固点型钢纤维在混凝土中含量提升，从0～1.6%，强度均呈增长趋势，其增长的强度至多达到7.19 MPa，增益效果比剪切型钢纤维更加明显。

由于这里所采用的钢纤维属性存在差异，根据所参考的文献[13]，立方体试件抗压强度

fcu=fcu,0(1+αvflf/df)

(1)

式中：fcu,0为素混凝土的实测强度；α为钢纤维影响系数；vf、lf/df分别为钢纤维掺入比例及长径比。

对试验过程中所记录的数据通过相关软件进行分析计算，影响系数α如表4所示。

表4 钢纤维对立方体混凝土强度影响系数α

如表4所示，混凝土强度等级越高，影响系数α则越小，式(1)中的fcu与α成正比，因此钢纤维对立方体强度的影响会由其自身强度提高而降低。

表5为计算与试验值的比例关系，可以得出二者比值与1十分接近，所以基于钢纤维影响系数来计算立方体抗压强度是可行的。

表5 抗压强度计算值和试验值对比

2.3 应力-应变全曲线

基于所有组试件记录的试验数据，所绘制的应力-应变全曲线如图5所示。

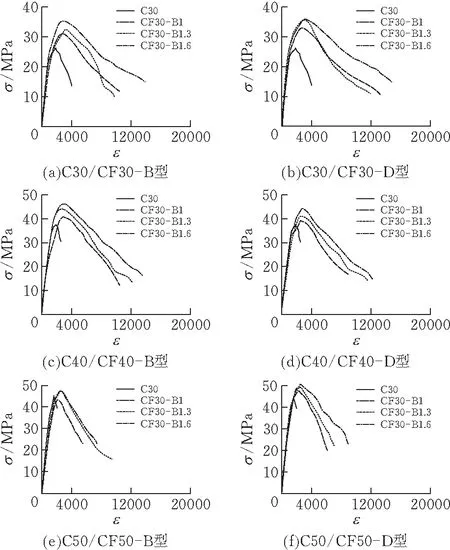
图5 应力-应变试验曲线

2.4 峰值应力与峰值应变

峰值应力体现了试件的受压时的极限承载能力，峰值应变的大小则取决于峰值前对裂缝不规律扩展的限制能力。钢纤维对峰值应力的影响规律与立方体试件的抗压强度相类似，因此不再赘述。峰值应变增量如表6所示，钢纤维分别能为C30、C40、C50强度等级的混凝土增加45.04%～73.04%、40.52%～51.45%、和27.91%～56.84%的峰值应变。说明钢纤维对各个强度混凝土的阻裂能力均有积极作用，在低强度时尤为显著。

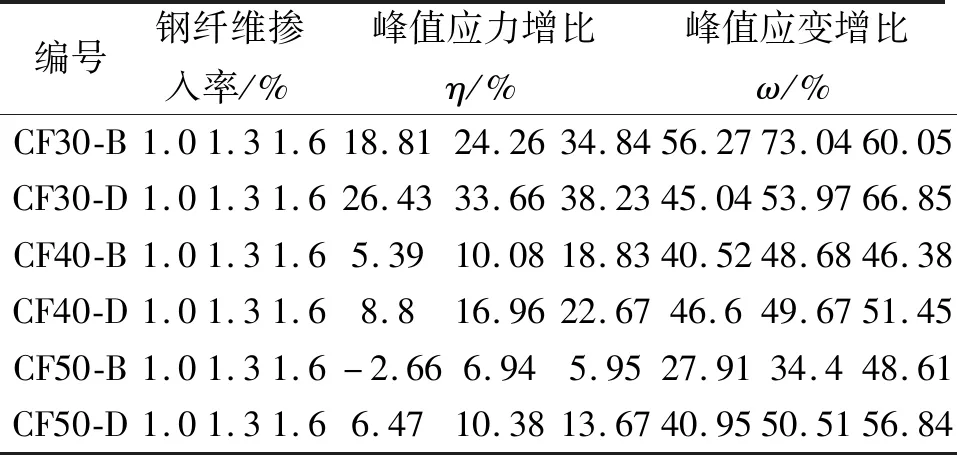
表6 钢纤维混凝土较普通混凝土峰值应力、峰值应变增量

由表6可知，η为钢纤维混凝土对照同强度普通混凝土峰值应力的增比，ω为钢纤维混凝土对照同强度普通混凝土峰值应变的增比，与钢纤维掺入率一一对应，计算公式分别为

η=(σ钢纤维混凝土/σ普通混凝土-1)×100%

(2)

ω=(ε钢纤维混凝土/ε普通混凝土-1)×100%

(3)

式(2)、(3)的下标限定条件为同强度等级。

2.5 极限压应变及残余应力

掺入1.0%～1.6%的剪切型钢纤维和多锚固点型钢纤维，分别能使混凝土的极限压应变达到规范[14]值0.0035的1.6～3.9倍和1.8～4.2倍，极大增强了混凝土的变形能力，多锚固点型钢纤维由于它在同样掺入率下，有更多的数量，外加扁平的中连段及扁平的两末端的共同桥接作用，其对混凝土极限压应变的改善要略好于剪切型钢纤维。

残余压应力体现在当结构应力达到峰值水平后，经过一段塑性变形后所残留的承载能力。由表2可以得出，在0.01时的压应变残余强度与钢纤维掺入率呈正相关关系。当混凝土为C30、C40强度，多锚固点型钢纤维残余强度可达到极限强度的35.6%～70%，在相同条件下其数值均高于剪切型钢纤维，多锚固点型钢纤维对混凝土残余应力的影响较剪切型好。

由于试验机自身刚度以及较高强度混凝土的脆性比较大，无法使C50强度混凝土压应变达到0.01。因此想要对比不同钢纤维对C50强度混凝土韧性的影响，需要结合应力-应变曲线并采用相应模型，通过软件进行分析计算。

2.6 韧性指数

依据文献[15]所给出的韧性计算模型如图6，A为峰点，C为下降段一点，值取峰值应力的50%，韧性指数为下降段AC与下轴线围成的面积S2同上升段OA与下轴线围成面积S1的比值。计算所得到的结果如表7所示，将钢纤维的掺入率从1%提升至1.6%，各组试件韧性指数均有明显的增加，钢纤维掺入率的提高能有效改善混凝土的韧性。

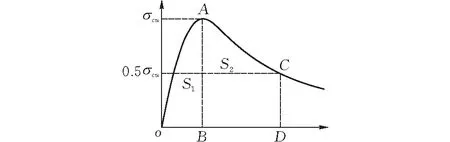
图6 韧性计算模型

表7 韧性指数实测结果

表7为各组试件韧性指数平均结果，可见混凝土韧性会受到钢纤维类型、掺量及自身强度的影响。在CF30和CF40强度下，多锚固点型钢纤维对混凝土的韧性有更好的影响结果，在CF50强度下，剪切型要比多锚固点型钢纤维更佳，如图7所示。

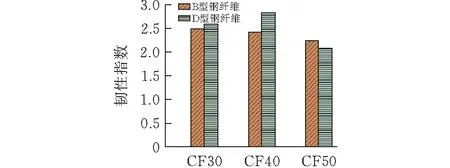
图7 韧性指数平均值对比

3 结论

1)钢纤维掺入率的提高能使结构韧性有所提升，对比强度为CF30和CF40的混凝土的增韧效果，多锚固点型钢纤维优于剪切型，但在CF50混凝土强度下，剪切型钢纤维的增韧效果更好。

2)混凝土强度等级越低，则钢纤维对抗压强度的提升越高，二者之间呈现反比例关系，强度达到CF50时，随着剪切型钢纤维掺入率的增加，抗压强度可能增减不定。

3)通过对比可以看出,基于钢纤维影响系数所提出的混凝土抗压强度计算方法与试验结果有较好的吻合。