基于光谱梯度角的改进SREM融合方法

蒋彤，安如*，邢菲，王本林, 琚锋

(1.河海大学 水文水资源学院，南京 210098;2.河海大学 地球科学与工程学院，南京 211100;3.滁州学院 地理信息与旅游学院，安徽 滁州 239001)

0 引言

高光谱影像拥有较多波段，能够准确地反映不同地物特有的吸收或反射特性[1-2]。但由于受到成像机制的限制，高光谱影像通常空间分辨率较低，混合像元分布严重，且幅宽较小，在应用中有着局限性[3]。多光谱影像虽然波段数少，但幅宽较大，且空间细节信息丰富。针对高光谱影像和多光谱影像各自的优势，通过图像融合算法，将多光谱影像中的空间细节信息与高光谱影像中的光谱信息进行融合，获得同时兼具高光谱与高空间分辨率的融合影像，从而提高地物识别与特征提取能力[4]。

目前，常见的多光谱-高光谱融合算法主要分为3类。一是频率域滤波方式。二是基于概率统计理论的影像融合[5]。前者由于空间信息来源不一致，导致现有的高光谱-全色的融合方法适用性低[6]。后者在使用梯度下降法求解时，存在鲁棒性不高，计算复杂的问题[7]。三是最常见的基于混合像元分解理论进行数据融合。例如Yokaya等提出的联合非负矩阵分解方法(Coupled Nonnegative Matrix Factorization, CNMF)[8]。但现有的像元分解算法只利用了混合像元的光谱维信息，没有考虑像元的空间相关性[9]。基于非负矩阵分解的算法由于目标函数非凸性，对初值敏感，导致端元与丰度矩阵不稳定[10]，影响融合图像的质量。

上述三类常见的融合算法大多要求多光谱和高光谱影像完全重叠，无法对重叠范围之外的区域进行融合。Sun等人提出的多光谱图像光谱分辨率增强方法(Spectral Resolution Enhancement Method, SREM)[10]，实现了融合方法在空间上的扩展。根据重叠区高光谱纯净端元，进行支持向量机分类 (Support Vector Machine, SVM)并提取高光谱与多光谱数据集，计算转换矩阵，通过光谱加权最小距离筛选转换矩阵，实现高光谱图像重构，重构出的高光谱图像同时具有高光谱与高空间分辨率，且增加了幅宽。但在融合过程中，由于对图像进行了重采样和空间配准，较大的分辨率差、影像不同灰度属性或对比度使得配准出现困难，对像元的位置和信息量造成影响[11]。

针对以上问题，本研究提出了改进的多光谱图像光谱分辨率增强方法(Improved Spectral Resolution Enhancement Method-Spectral Gradient Angle, ISREM-SGA)，其主要思想是通过计算高光谱影像上像元光谱，与多光谱影像上对应位置及其邻域内像元光谱的梯度角，匹配同名点，来获得最具光谱相似特性的光谱数据集，进行高光谱图像的重构。本研究以意大利帕维亚大学Pavia U(Pavia University)、 日本筑西市Chikusei的高光谱图像为例，对两组原始高光谱数据进行空间和光谱上的降采样生成模拟的高光谱、多光谱实验数据进行融合研究，最后对融合图像进行质量评价。

1 研究数据

本研究选取两组空间变异度差距较大的高光谱图像为研究数据。数据集1为2014年7月获得的Chikusei高光谱图像，如图1a(1)所示，由美国Headwall公司通过可见光-近红外C系列高光谱传感器拍摄生成。此次研究只选用400×400大小的图像作为基础数据，图像的空间分辨率为2.5 m，波长范围为 0.360～1.018 μm，共128个波段。图像上共有部分水体、7种植被、3种裸土以及8种人造物这19类地物[12]，但图像主要以耕地为主，空间变异度低，光谱特征差异小。Chikusei 数据下载地址：http://park.itc.u-tokyo.ac.jp/sal/hyperdata/。数据集2选用的是2003年成像的意大利北部帕维亚大学Pavia U数据，如图1b(1)所示。该高光谱数据是由机载反射光学光谱成像仪传感器拍摄生成，共包括从0.43～0.86 μm的103个波段，每个波段上像元总数为610×340，图像的空间分辨率为1.3 m，图像包含沥青道路、砖石、金属板、柏油房顶、草地等9类地物[12]。数据集2是以居民地和交通用地为主，地物类型少，但各光谱特征之间差异较大。Pavia U下载地址：http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes。

图 1 实验数据Figure 1 Experimental Data

表 1 Chikusei与Pavia U数据多光谱波段信息Table 1 Multispectral band information of Chikusei and Pavia U

对数据集1和2进行光谱降维，利用光谱变换矩阵模拟出多光谱图像，如图1a(2)和b(2)所示。光谱变换矩阵根据多光谱图像各波段的光谱响应函数得出，两组数据均以环境与灾害监测预报小卫星A星(HJ-1A) CCD多光谱数据的光谱响应函数为参考，具体操作如下：(1)对每一条光谱响应函数在原始高光谱数据中心波长处进行重采样，并计算采样值在各中心波长处的权重；(2) 根据权重对高光谱图像的波段数进行加权求和，得到模拟多光谱图像。模拟出的多光谱图像拥有4条波段，各波段的详细范围展示在表1中。

对两组数据集的原始高光谱数据进行降采样，获得空间分辨率较低的模拟高光谱数据，对模拟结果进行裁剪，获得与多光谱图像仅有部分重叠的高光谱图像用于融合实验。为保证提取到相同位置的像元光谱，利用最近邻法将高光谱图像重采样成多光谱图像大小，并进行空间配准，结果展示在上图1a(3)、b(3)中。但Chikusei 、Pavia U高光谱图像在前5个波段出现下图2中a(1)、b(1)所示的明显噪声点，a(3)、b(3)信噪比结果图中也表明其信噪比略低，因此只选用剩余无明显噪声点的波段作为最终融合实验所用的高光谱图像。

2 研究方法

2.1 多光谱图像光谱分辨率增强方法:SREM

由于高光谱图像与多光谱图像在重访周期和幅宽上都有着明显的差异，大多数融合方法受到覆盖范围的限制，但尽管如此，不同传感器拍摄的图像上同类地物在光谱信息上仍具有一定的相似性。基于这一原理， Sun等人提出了SREM多光谱图像光谱分辨率增强方法。在SREM方法中首先利用顶点成分分析(Vertex Component Analysis, VCA)算法获得高光谱图像端元，并根据纯净端元对高光谱图像进行SVM分类，根据分类结果提取在空间位置上相互对应的各地物高光谱数据集、多光谱数据集。对于有着N类地物的图像而言，可分别用下式(1～2)的矩阵M(q)、H(q) 来描述第q类地物的多光谱与高光谱数据集：

(1)

(2)

式(1～2)中：M(q) 是维度为L×W的矩阵，H(q) 是维度为K×W的矩阵L与K分别表示多光谱和高光谱波段数，W表示提取像元的个数，W的值不得小于多光谱的波段数,否则无法提取足量用于影像重构的光谱和空间信息。

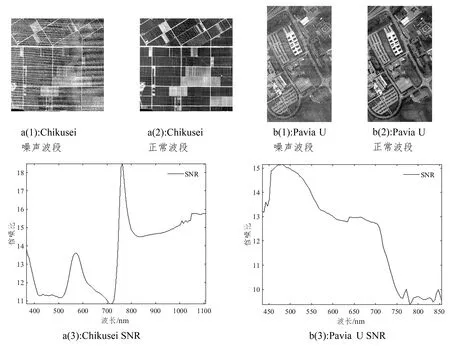
图 2 高光谱图像信噪比与噪声波段Figure 2 SNR and noisy band of hyperspectral image

G(q)=H(q)M(q)T(M(q)M(q)T)-1

(3)

h(q)=G(q)×M(q)

(4)

其次计算转换矩阵。Winter等人在提出的CRISP方法[14]中表示，可以通过移动窗口提取光谱数据集，并根据最小二乘方法即公式(3)计算窗口对应的转换矩阵，将得到的转换矩阵按照公式(4)计算重构高光谱影像。

最后对转换矩阵进行逐像元筛选，实现高光谱影像的重构。通过计算光谱加权最小距离 (Spectral Angle Weighted Minimum Distance, SAWMD)，即按照公式(5～8)将h(q)与高光谱数据集的均值向量进行匹配：

(5)

(6)

(7)

SAWMD(q)(i)=EMD(q)(i)·[1-cos(SAM)(q)(i)]n

(8)

式(5～8)中：EMD(q)(i)表示的是h(q)(i)中第i个重构向量与均值向量的之间欧氏距离；SAM(q)(i)表示两个向量的光谱角；参数n用于调节光谱角的权重，一般取值为1。光谱距离越小，表明结果越精确。按照公式(10)逐像元筛选转换矩阵，实现高光谱影像的重构，重构高光谱拥有多光谱图像的空间分辨率和幅宽。

(9)

SAWMD(q)(i)=min(SAWMD(1)(i),SAWMD(2)(i),…SAWMD(N)(i)

(10)

2.2 聚类后聚合的光谱分辨率增强方法:ISREM-SGA

在提取光谱数据集时，将高光谱图像重采样成多光谱影像大小，以提取对应位置的像元光谱。但重采样会导致像元发生变化，例如在使用最近邻插值时，像元产生半个位置的偏移；使用双线性内插时也会破坏像元信息量，影响波谱分析[15]。在进行空间配准时，配准影像的多源性与环境复杂性，也会导致较难获得精确对准的像元点[16]。为了改善上述不足，本研究提出一种基于光谱梯度角的改进ISREM-SGA高光谱-多光谱图像融合方法。具体操作如下：(1)按照SVM高光谱图像分类结果，提取高光谱像元光谱，并根据光谱变换矩阵进行降维。(2)计算降维后高光谱像元光谱，与多光谱影像上对应位置及其邻域内像元光谱的梯度角来匹配同名点。计算光谱梯度角需对2个光谱向量先进行一阶求导，获得其梯度向量，再计算2个梯度向量的广义夹角[17]，光谱梯度角的计算如式(13)所示。该方法能够反映光谱特征变化的优势，特别是对光谱曲线斜率的变化。将最小梯度角对应的像元作为该高光谱像元最佳匹配点，提取出最具相似光谱特性的多光谱数据集。(3)按照上述公式(5～10)逐像元实现高光谱影像重构。

SG(x)=(x2-x1,x3-x2,…，xn-x(n-1))

(11)

SG(y)=(y2-x1,y3-y2,…，yn-y(n-1))

(12)

(13)

3 结果与分析

3.1 影像视觉效果分析

融合图像的质量决定了图像应用的广泛性，选取SREM和ISREM-SGA方法与常用的CNMF融合和Gram-Schmidt融合(以下简称 GS融合)[18]进行对比，其中CNMF与GS融合采用的是覆盖范围一致的高光谱和多光谱影像。彩色合成后的Chikusei(RGB分别对应波段60(667 nm)、40(564 nm)、20(467 nm))和Pavia U(RGB分别对应波段103(857 nm)、63(687 nm)、29(531 nm))融合图像展示在下图3中 。

图 3 Chikusei与Pavia U彩色合成图像Figure 3 Color composite images of Chikusei and Pavia U

从图3中可以发现，ISRME-SGA融合影像的视觉效果与参考图像比较接近，影像清晰，纹理特征与边缘特征明显，且色彩信息与参考图像基本保持一致，不受空间变异度的影响。SREM方法生成Pavia U影像的植被和建筑物亮度值变低，发生了明显的色彩畸变，而ISREM-SGA缓解了这一问题。主要原因在于通过光谱梯度角提到的数据集，最具相似光谱特性，能够有效地代表此类地物，从而获得质量更高的转换矩阵用于影像重构。ISREM-SGA方法与CNMF方法生成的融合影像，在视觉效果上与参考图像最为相似，但ISREM-SGA在仅依靠重叠区域光谱和空间信息的基础上，生成了高质量融合影像，更具优势。在图3中可以发现，ISRME-SGA融合影像在视觉效果上与参考图像比较接近，影像清晰，纹理特征与边缘特征明显，且色彩信息与参考图像基本保持一致，不受空间变异度的影响。SREM方法生成Pavia U影像植被和建筑物亮度值变低，发生了明显的色彩畸变，而ISREM-SGA缓解了这一问题。主要原因在于通过光谱梯度角提到的数据集，最具相似光谱特性，能够有效地代表此类地物，从而获得质量更高的转换矩阵用于影像重构。ISREM-SGA方法与CNMF方法生成的融合影像，在视觉效果与参考图像最为相似，但ISREM-SGA在仅依靠重叠区域光谱和空间信息的基础上，生成了高质量融合影像，更具优势。

3.2 典型地物光谱分析

分别提取4种融合影像的植被和建筑物光谱曲线，比较融合方法间的差异，光谱曲线如图4所示。在图4的光谱曲线对比中可以发现，在ISREM融合影像上提取的植被和建筑物光谱曲线，与参考光谱变化趋势基本一致。从上图2信噪比变化曲线中可以看出Chikusei影像在430～500 nm、700～730 nm，Pavia U影像在760～850 nm范围内高光谱波段的信噪比要小于其他波段，较低的光谱信息质量导致光谱间产生差异。其中植被光谱相较于建筑物光谱误差小，建筑物由于材质不同，拥有不同的吸收或反射特性，对像元位置偏移敏感。在SREM生成的Pavia U融合影像中，受到像元偏移与复杂场景内容的影响，纯净端元获取困难，在进行SVM分类时，影像无法识别建筑物纯净光谱，导致缺少相应的光谱数据集，融合后建筑物光谱在除红光之外的波段都发生明显的畸变。尽管如此，ISREM方法的误差值也要远小于SREM方法的误差，由此说明了ISREM方法对比原方法有了一定的改善。

图 4 典型地物光谱曲线对比Figure 4 Comparison of spectrum of typical features

3.3 融合影像质量统计分析

统计指标上本研究选择了相关系数R[19]、通用图像质量指标(Universal Image Quality Index, UIQI)[20]、相对全局无量纲误差(Erreur Relative Global Adimensionnelle Synthese，ERGAS)[21]、结构相似度(Structural Similarity Index，SSIM)[22]、光谱角(Spectral Angle Mapper ,SAM)[23]对融合影像进行质量评价。一般认为R、UIQI、SSIM值越接近1图像失真越少，ERGAS和SAM则是值越小融合质量越高。公式如下，计算结果见表2。

表 2 融合图像质量评价Table 2 Evaluation of fusion image

(14)

(15)

(16)

(17)

(18)

式(14～18)中：x表示融合图像，y表示原始高光谱数据，x与y表示波段均值，σxy表示协方差，σx与σy表示方差，表示光谱向量的内积，‖x‖、‖y‖表示光谱向量的范数，C1、C2是避免分母为0的常数，h、l表示多光谱图像与高光谱图像的空间分辨率，RMSEK表示均方根误差，μK表示第K波段参考图像的均值。

从表2中可以看出ISREM-SGA对比原方法，在空间和光谱指标上都有所提升，其中Chikusei影像质量略有提升，Pavia U影像在空间和光谱上的提升较明显，R、UIQI、SSIM值分别增加了0.237、0.297、0.238，ERGAS、SAM值分别降低了35.81和7.312，具有较强的空间和光谱信息保持能力。ISREM-SGA对比CNMF融合差距较小，但ISREM-SGA方法只使用了部分重叠影像，运算时间更短。相较于GS融合，ISREM-SGA在两组数据集上都取得了较好的融合效果，更具稳健性。选取融合前后每组对应波段内全部像元计算相关系数与信息熵(图5)。从图5中可以看出ISREM-SGA融合结果虽然在个别波段的值较低，但整体上有所提升，如450～700 nm、760～830 nm处，相关系数均在0.90以上。在相关系数差距大的波段，如900～950 nm处，信息熵也有明显的差异，虽然熵值较大，但承载的是离散信息，在实际应用中可以去除这些异常波段，以扩大应用范围。

图 5 相关系数与信息熵对比Figure 5 Correlation coefficient and information entropy

为进一步比较各方法的光谱信息保持能力，进行光谱角制图[24]， 图像中像元值代表光谱角大小，颜色越明亮光谱角越大(图6)。通过光谱角制图结果可以看出ISREM-SGA对比SREM方法，影像中框选的地物混合分布区和建筑区的光谱角降低，可较好地保持光谱信息。对比CNMF融合，ISREM-SGA的方法略有逊色，主要原因在于CNMF方法无须考虑重采样和空间配准造成的像元位置偏差，对像元分解的过程以及波谱分析的影响。

图 6 各融合方法光谱角制图 Figure 6 SAM map of different methods

为了衡量融合方法在空间信息上的保持能力，对融合结果进行主成分变换。由于融合前后的影像在第1、2主分量中信息量都比较丰富，较难验证融合后增加的空间信息量，因此在图7、8中展示变换后的第3、4主分量。根据主成分分量显示图，融合前影像的分量虽然可以看出部分纹理特征，但影像较模糊。SREM与ISREM-SGA融合方法虽然只使用重叠区域的空间信息，但对比其他清晰度增加，生成的Pavia U融合图像，在图8中框选的区域可以看出明显的改善，表明了ISREM-SGA具有较好的空间信息保持能力，相较于其他融合方法有着一定的优势。

4 结论

采用ISREM-SGA融合、SREM融合、CNMF融合、GS融合进行高光谱-多光谱的融合实验，并对融合图像进行光谱和空间信息质量评价。评价结果表明：基于光谱梯度角的ISREM-SGA融合方法，光谱信息和空间信息保持能力较好，具有很好的稳健性。与CNMF融合方法相比，融合图像效果相似但运算时间更短。ISREM-SGA方法通过光谱梯度角对像元光谱进行匹配，能够准确地提取对应位置的光谱数据集进行融合研究，缓解了像元位置偏移造成的光谱畸变问题，提高了融合图像质量。

但本方法仍存在不足，如重采样的方法只选择了最近邻法，没有对比影像在双线性内插和三次卷积内插时融合结果的质量。在今后的研究中，仍将进一步改进。

图 7 Pavia U主成分变换后第3、4分量Figure 7 PC3,PC4 of Pavia U

图 8 Chikusei主成分变换后第3、4分量Figure 8 PC3,PC4 of Chikuse