ART算法的改进及在Shepp Logan头模型的应用①

陈正慧，韦民红

(淮北师范大学物理与电子信息学院，安徽 淮北 235000)

0 引 言

CT(industrial computed tomography)技术的核心是投影重建图像的理论，现在图像重建的方法主要有解析和迭代算法[1]。迭代算法近几年来由于计算机的高速发展，重建速度作为其最大的缺点得到了很大的改善，这个缺点已经不再制约着迭代算法的发展，因此迭代算法再度引起了人们的关注。

为了进一步的发展，中国工程物理研究首先建成了基于反应堆的冷中子和热中子CT装置，并取得了研究成果，这个装置也是以解析算法为重建算法。但是在人们的实际生活中，经常有一些奇形怪状的样品，这些样品不能完整的获取投影数据，这就是解析算法的短板了，解析算法对于投影数据的完整性要求性高，如果仍用解析算法的话难以得到理想的重建效果了。因此迭代算法在CT中的研究和发展就势在必行了。迭代算法最具有代表性的是ART算法，改进ART算法也就成为了研究热点[2-3]。

1 模拟退火算法

模拟退火算法最开始是Metropplis等一批学者提出来的[4]。这是由物理中固体的降温过程启发而来的。这个算法具有较好的鲁棒性和全局收敛性。该算法主要有以下三个过程。

加温过程。粒子在高温的时候具有较高的能量，给粒子比较高的温度，这样粒子就会重新排序并且会偏离原来的平衡位置。

等温过程。这个过程中系统封闭，在系统中，粒子会慢慢往自由能小的方向自发转化，但这个过程中温度不变而且会与周围环境交换热量,最终粒子会降到自由能最小，而这就是粒子达到平衡的过程。

图1

冷却过程。这个过程就是降温的过程，当粒子完全冷却时就会形成低能状态的晶体。

值得注意的是，这个等温过程就是算法Metroplis的抽样过程，而最重要的也是这个过程，这个也是模拟退火能得到全局最优解的关键，模拟退火以较低的概率接受恶化解，较高的概率接受优解。这样就可以跳出局部最优解而得到全局最优解。

假设是解决一个寻找最小值得优化问题，模拟退火寻优算法就是将模拟退火的思想应用在寻优问题上。

如果想要优化这样一个函数F:x→R，x∈A，x是优化问题其中的一个可行解，R={y|y∈A,y>0},定义域用A表示，N(x)⊆A就是x的一个邻域集合。

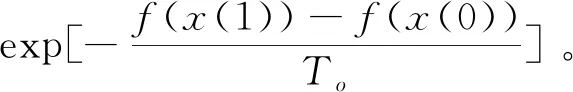
值得注意的是，降温的过程得足够慢，不然最后很可能错过最优解，得不到全局最优解。

2 CRRT算法原理

首先把目标图像f(x,y)看成是一个包含N个网格的正方形网格，其中N=n×n。

如图1所示。

这样划分的其中一个小网格就可以看成一个像素，小网格的内部f(x,y)可以当成一个常数值，射线就以一定的方式射入待测目标图像的区域网格，对应的投影值pi就可以表示为第i条射线。目标图像重建的问题就转化为了一个线性方程组

(1)

这里的M是射线的总线条数，N表示总的单元格数，N=n×n,有n行n列。而式中的f'j是对第j个单元格的真实像素fj的估计值。Wij是加权因子，这时候要解决的关键问题是求取加权因子Wij，在这里先设单元格的宽度为ε，而设射线的宽度是0。把单元格第i条射线和第j个像素相交的长度的比值定义为Wij，Pi表示第i条射线的线积分，这个也就是投影数据。

峰值信噪比

(2)

t为图像的位数，m和n分别代表图像的高度和宽度；I，K分别为参考图像和迭代图像。P值越大，表示重建效果越好。

归一化平均距离判据

(3)

Ii,j表示参考图像第i行第j列的像素浓度，Ki,j表示重建后第i行，第j列的像素浓度。r的值越小，表示误差越小，重建的效果越好。

CRRT算法步骤如下：

(1)取图像的初始估计值fj0=0(一般取0);

(2)根据模拟退火算法的原理，随机选取一个松弛因子λk,这个松弛因子应该服从正态分布(λ0,1/k)。k是迭代次数，λ0选取的是0.25。

(3)迭代算法如下:

(4)

(4)迭代接受判别依据

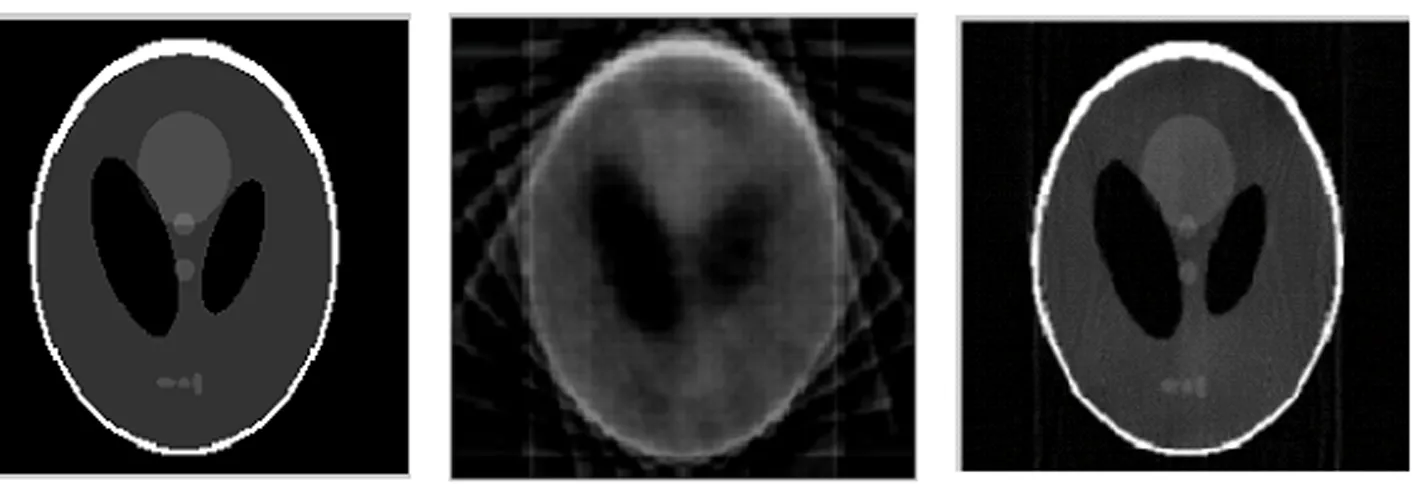
图2 原始头模型 图3 传统算法 图4 CRRT算法

如果Pk+1>Pk,说明这一迭代结果比上一迭代结果好，选的松弛因子比较合适，可以继续下一步迭代。反之，如果Pk+1>Pk，说明迭代朝着恶劣的结果发展，就放弃该次迭代结果。

(5)算法结束依据

如果||fjk+1-fjk||<ξ(ξ很小，一般取10-6)，结束算法，这个fjk+1就是这次的重建结果。

3 CRRT算法的检验与结果

使用MATLAB实现了该次实验，实验选用了Shepp Logan[5]头模型，Shepp Logan头模型是一个大的椭圆里面有九个小的椭圆，而且这九个椭圆的位置和大小都不一样，这个Sheep Logan头模型就像是一个人体大脑断层图像。实验重建的Shepp Logan头模型大小是180×180，探测元的个数是260个，取180个投影角采样。用文中的算法和传统的算法进行了对比[6-9],实验结果如图2-4所示。

由图2、图3、图4所示，传统算法相比较于CRRT算法有较明显的伪影和模糊，这是人们肉眼可以观察得出来的，但是肉眼观察会有误差，也无法用数据证明，所以用归一化平均距离判据r作为评判标准，并将传统算法和CRRT算法的归一化平均距离判据r作为对比，得出的数据如图5所示。

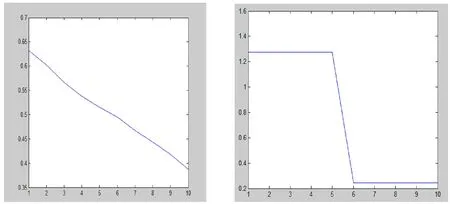
a 传统ART算法 b CRRT算法

图5中a图是r迭代了十次的变幻趋势，可知r一直趋于稳步降低的趋势。图5中b图是CRRT算法迭代了十次后再优化了十次松弛因子，由实验数据可知，在选到更好的松弛因子后，r值明显降低并趋于平稳状态。

实验结果表明，CRRT算法可以优化松弛因子。

4 结 论

将ART算法和模拟退火相结合，采用模拟退火来优化ART算法的松弛因子。结果表明，新的算法明显比传统算法的伪影要少的多，图像的质量也比较好。值得指出的是，实验采用的是模拟退火算法优化的松弛因子，今后的研究可能还会有更好的优化算法来替代模拟退火算法。