基于逆向拍卖模型的群智感知激励机制①

胡婷婷，朱晓娟

(安徽理工大学计算机科学与工程学院，安徽 淮南)

0 引 言

近些年来，随着无线传感网络和社交网络的快速发展，大量的智能手机、智能手环、pad等手持移动设备的激增，催生出了一种可以对物理世界进行数据收集的感知范式-----群智感知( Crowd Sensing， CS)[1]。群智感知利用大规模用户的移动设备上搭载的传感器来进行数据的感知和采集工作。移动用户可以将收集到的数据上传到服务器而不会产生任何重大成本。例如，用户可以利用社交网站(例如大众点评)来点评对商家的满意度等指标。群智感知在物联网的很多领域都有着重要的应用，如环境监测、智能交通、城市管理等[2]。用户在参与感知任务的过程中由于受到设备的电量、存储空间的限制,有些感知任务可能会造成位置隐私泄露问题，这就会导致有些用户不愿意参与到感知任务中来[3]。因此，设计一种可以激发用户积极性的激励机制，吸引更多用户来参与感知任务尤为重要。

目前的激励形式主要分为报酬激励和非报酬激励[4]。报酬激励即利用金钱来鼓励参与者参与任务；非报酬激励则采用诸如虚拟积分、社交关系等方式来吸引一批有共同爱好和兴趣的人参与进来。现有的激励机制大多以平台为中心[5]，侧重于如何选择用户来进行报酬支付以最大化平台效益为核心，而忽略了用户考虑到自身利益不愿意积极参与感知任务而导致任务分配率不高的问题。在保障用户利益的前提下，提高参与人数的同时保证服务器平台所需任务是有待研究的重点。为此，提出了一种基于逆向拍卖的激励机制来解决以上问题。

1 相关工作

近些年来，国内外学者对群智感知激励机制做了大量的研究。Luo[6]基于用户之间的协作任务，提出了一种合作众包拍卖机制实现最小化支付；Duan[7]等人通过建立Stackelberg博弈模型，基于用户间的协作行为而制定了一套奖励机制；Peng[8]等人从用户上传数据质量的角度出发来避免无效、低质数据，再利用最大似然估计和贝叶斯算法来选择高质量用户，最大化平台收益；以上机制中平台占据主动权，用户处于被动状态，这种情况下往往参与率不高。Ke[9]等人考虑从用户敏感位置隐私安全的角度进行着手，来促进用户参与的积极性；Yang[10]等人则是分别从以平台为中心和以用户为中心建立了两种模型机制，一种以平台为中心利用 stackelberg game 设计激励机制，根据用户的时间因子来进行判断；第二种则以用户为中心建立逆向拍卖机制Msensing，相比于前者增大了用户的主动性，但在优胜者选择的时候采用贪心法，任务覆盖率考虑不足。

以上的激励机制从用户质量、信誉奖励和隐私等不同的角度去激励用户积极参与感知项目。文中则侧重从提高用户效用的角度出发，刺激参与人数的增长，从而起到提高用户参与率并且希望用户上传的数据符合平台要求任务的目的。

2 系统模型及问题描述.

逆向拍卖又被称为反向拍卖和荷兰式拍卖，不同于正向拍卖一个卖家叫价，多个买家竞拍的模式，逆向拍卖则和正向拍卖相反，是一个买家和多个卖家的竞拍方式。对应到群智感知系统中，买家就是服务器平台，而卖家则为持有感知任务的用户，见图1。服务器平台进行广播所需要的感知任务，用户则根据手上平台所需数据来参与竞拍，服务器平台再根据用户提报的竞标价和任务本身的价值来进行综合考虑，最终给予符合条件的用户报酬激励。

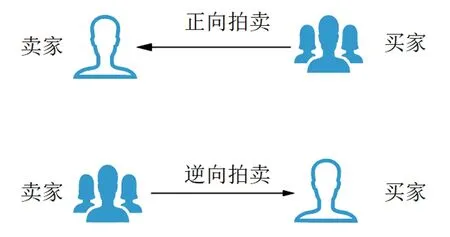
图1 正向拍卖与逆向拍卖的区别

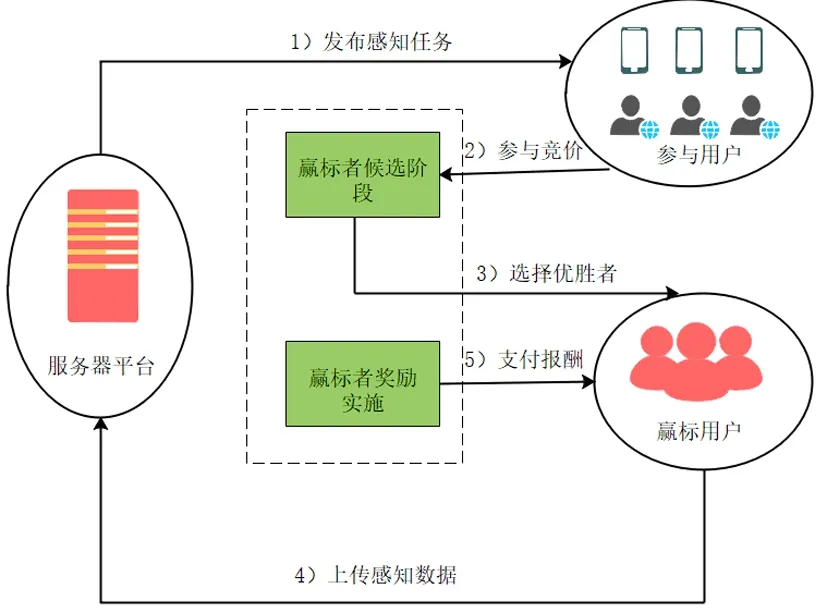
图2 基于逆向拍卖模型

2.1 系统模型

服务器平台发布任务后，卖家根据自身设备收集到的数据来参与竞标。如图2所示。服务器平台发布感知任务集Γ={τ1,τ2,…τm,},m为平台发布的总任务数，τi为彼此独立的任务。并且定义平台发布的任务集合所对应的价值集合为V={v1,v2,…vm};对任务感兴趣的用户U={u1,u2,…un,}参与竞价，用户ui(i=1,2,…n)所提交的任务子集Γi⊆Γ和自己的竞标任务对Bi=(Γi，bi)，其中bi为用户提交的竞标价格；设用户在参与竞标中耗费的成本为ci,且成本只有自己知道，对用户和平台都是不透明(ci≥0且ci≤bi)。任务平台来选择优胜者集合，即赢标用户集W⊆U,并将优胜结果告知参与用户；赢标者上传平台所需的感知任务，感知平台为每个优胜者根据用户ui完成的任务Γi支付胜出者报酬pi(pi≥bi)。

2.2 问题描述

激励机制通过赢标者候选和赢标者支付两个步骤来实现，在选择赢标者阶段，通过每个任务都至少对应一位成功执行任务的用户来进行判决赢标者。当完成某个任务的用户数量仅为一人时，则直接选出优胜者集合W′；当完成某个任务的 人数大于等于2时,选择出的优胜者集合记为W″;平台将W′和W″的集合并在一起给总的赢标者集合W进行报酬支付。最后从计算的效率、个体理性、可行性和真实性来判断该机制的性能和效用。

其中用户ui的效用可以表示为平台的支出报酬pi与用户消耗的感知成本ci之间的的差值，即

(1)

其中W为赢标者集合；当用户落选赢标集时，效用则为0。落选的用户可以选择退出或进行下一轮任务的竞拍，多轮竞拍的情况这里不做考虑。

服务器平台的效用u0则为优胜者W完成任务的总价值与支付赢标者报酬之间的差值，即

(2)

2.2.1 赢标者候选阶段

在逆向拍卖机制中，参与者的竞价bi要参考在参与任务中的消耗成本ci，而任务发布平台则要考虑到以最大化平台效益选取赢标者集合来进行支付，在之前的研究中，已经被证明此类型为NP-Hard问题[11]，即无法在多项式内得到最优解集合。需要换个思路来解决这个问题，当任务集覆盖的竞标用户数量ni=1时，只要用户的上报竞标价格bi与其提供的任务总价值vi的比值小于1，则该用户就为此任务的优胜者；当任务集覆盖的竞标用户数量ni≥2时，对用户的竞标价格bi与其提供的任务总价值vi的比值进行一个排序，且小于1的用户作为优胜者集合，最终选出符合条件的赢标者集合W。

公式如式(3)：

(3)

算法一:任务选择算法输入:任务集Γ,价值集V,所有竞标用户上报的任务集Γ',竞标任务对Bi=(Γi,bi),赢标集W= I;输出:赢标者集合W,赢标者集合中所覆盖的任务集合Γ''1:for allτi in Γ' do2:if (ni=1&bi≤vi)then3: W'←W'∪ui ,Γ″←Γ″∪τi /* W'为从竞标者数量ni=1的任务集中选出的优胜者*/4: if (ni≥2)then5: Sort(bi/vi)升序排列,见公式(3)6: 记,bs/vs←argmin(bi/vi)/* bs/vs为bi/vi中的最小值*/7: bh/vh←argmax(bi/vi)/*bh/vh为bi/vi中的最大值*/8: and if bivi≤1 then9: W″←W″∪ui ,Γ'←Γ″∪τi * W″为从竞标者数量ni≥2的任务集中选出的优胜者*/10: W←W'∪W″11:Endfor

2.2.2 赢标者支付阶段

选择完赢标者后，接下来要对其进行报酬的支付。根据梅尔森[12]的理论可知拍卖机制要符合以下两点要求：1)选择规则是单调的：如果用户i通过出价bi赢得拍卖，它则也通过出价bi’≤bi赢得。 2)每个赢标者都获得了关键价值：用户出价不会高于平台设定的某个阈值，则赢得竞标。

但目前的奖励措施大多采用统一支付的方式，不利于区分用户贡献。基于此，采取在多人竞标的优胜者集合W''里选取bi/vi比值最高者(后面统称为第一名)附加奖励的方式来进行报酬支付；其他的赢标者Wvi则采取统一支付的方式。由算法一第6行和第7行可知bs/vs为排序中的最小值，bh/vh为排序中的最大值。可以根据以下函数来设定奖励金：

TWs=vs(bh/vh-bs/vs)

(4)

其中TWs为第一名的附加奖励支付函数，vs为第一名提供的任务价值。

(5)

其中pi为总的支付函数。可以看出，在支付阶段没有采用统一支付的方式，而是给予了候选阶段中排序最低的bs/vs附加奖励，这种方式可以刺激更多的用户积极参与竞标任务。伪代码实现过程见算法二：

算法二:赢标者支付算法输入:赢标者集合W,赢标者集合中所覆盖的任务集合Γ'',赢标者集合中覆盖任务集的总价值奖励VΓ'', bi/vi中的最大值bh/vh支付报酬pi1:for all τiin Γ'' do2:计算3: if(bi/vi=bs/vs)then4: 根据(4)式计算出TWs的值5: for all ui∈W6: 根据(5)式计算出pi7:p=∑ui∈wpi/*p为支付的总报酬*/8:if (p>VΓ'') then 9: W‖p|010:输出pi11: endfor

2.3 性能分析

根据文献[13]可知，基于竞拍的模型激励机制的设计要满足计算效率、个体理性、可行性和真实性这四个指标。

(1)计算效率：指设计的方案可以使问题可以在多项式内解决。

(2)个体理性：用户的回报要高于付出的成本。

(3)可行性：服务器平台要保证自身效益非负，所支付的报酬小于任务的总价值。

(4)真实性：没有一个用户可以用不同于自身价值的竞价去提高自身效用。

证明1 该激励机制满足计算效率

由算法一可知在对任务τi进行遍历的for循环里的时间复杂度为O(m)，对bi/vi的排序算法的时间复杂度为O(nlogn)，所以总的算法复杂度应为(mnlogn)；算法二里对任务〗τi和用户ui进行for循环遍历，其时间复杂度分别为O(m)和O(n)。综上可见，算法都是在多项式时间内进行求解的，所以该机制是满足计算效率的。

证明2 该激励机制满足个体理性

用户竞标失败的情况下，则成本ci和报酬pi都为0，用户没有损失；而如果竞标成功的情况下，用户的报酬支付由(5)计算可以得到且ci≤bi,用户效用是非负的，所以该机制是满足个体理性的。

证明3 该激励机制满足可行性

若W=0，则没有符合的竞标参与者，用户U则为0；若W≠0，由算法二第8行可知，只有当平台需要支付的总报酬p大于赢标者提供任务的价值VΓ'时，才会启动程序，从而保证平台的效用非负，所以该机制是满足可行性的。

证明4 该激励机制满足真实性

根据Myerson的定律来进行证明

1)单调性：赢标者的条件由算法一第5行的排序可知是按照bi/vi排序大小的方式来的，即使用户提出小于bi的竞标价，但由于任务本身的价值vi并没有发生改变，所以依然是符合单调性的。

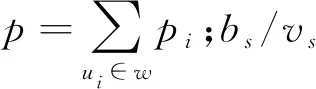
综上可知，所以该机制是满足真实性的。

3 仿真实验与分析

3.1 实验设置

为了去评估激励机制的效果，用Matlab进行了仿真实验，并且与文献[10]中的Msening算法进行了部分对比实验，使得结果更加直观可见。参数设置见表1。

表1 仿真参数设置

3.2 评估依据

将从平台效用、用户效用和任务覆盖率这三个方面来进行比较分析。

(1)平台效用：由式(2)可知为优胜者W完成任务的总价值与支付赢标者报酬之间的差值。

(2)用户效用：即所有赢标者总的效用与所有赢标者人数的比值。

(3)任务覆盖率：赢标者所覆盖的任务占到总任务的比例。

3.3 实验分析

1)平台效用。如图3(a)所示，随着任务数m的增加，两种激励机制的平台效应也相应的增加，这是因为用户在任务选择方面范围广，参与者为了增大自己的利益会选择价值任务高的，这也使得平台效用增加；由图3(b)可以看出，相比于Msensing机制后期平台效用略低的原因是，在报酬支付阶段里涵盖了给第一名优胜者额外支付的成本当用户数达到450-490的时候，任务基本分配，平台效应开始趋于稳定。

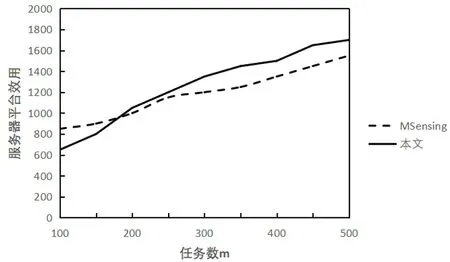
图3 (a)任务数与平台效用

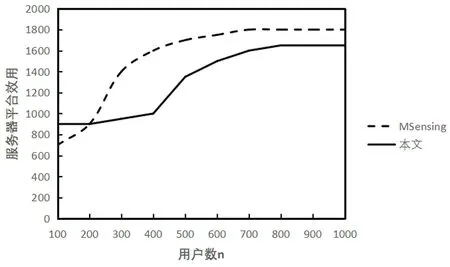
图3 (b)用户数与平台效用

2)用户效用。如图4(a)所示当最开始发布任务的时候，竞标者较多，赢标者数量增加，用户效用也相应的增加；随着完成任务的增多，即完成率超过任务总数m的一半时，用户完成任务的总价值已经趋向于稳定状态，从而曲线呈平稳状态；图4(b)中，用户数目的增加，竞争越来越激烈，随着任务完成率的提高，赢标者开始减少，用户效用趋于稳定。而机制中由于增加了用户的盈利，从而提高了用户参加任务的积极性。

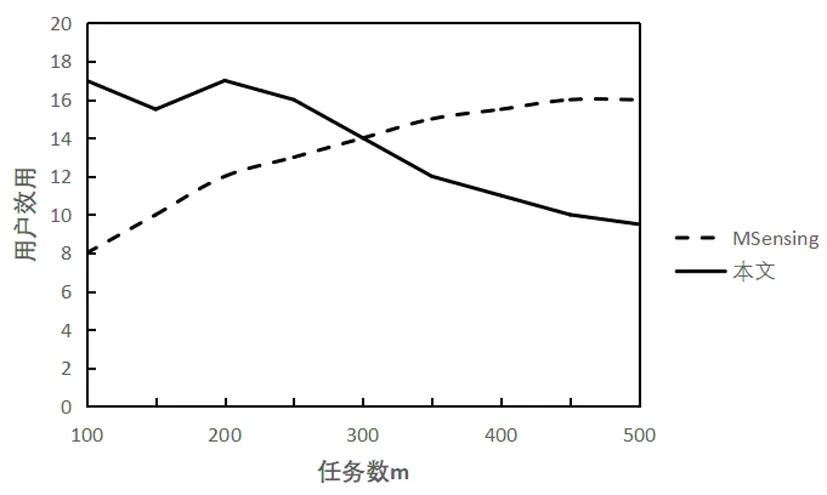
图4 (a)任务数与用户效用

图4 (b)用户数与用户效用

3)任务覆盖。如图5(a)所示。随着任务数的增加，MSening的任务覆盖率开始走低，主要是因为Msening在进行赢标者选择的时候采用贪婪法，不停地选择任务价值高和报价低的用户，在进行支付的时候，想要找到任务覆盖全的用户就比较难了；图5(b)中，随着用户的增多，当用户数n>任务数m时，基本上平台任务数已经覆盖完全，曲线趋于平滑。所以本机制在任务覆盖方面也是占优的。

图5(a) 任务数与任务覆盖率

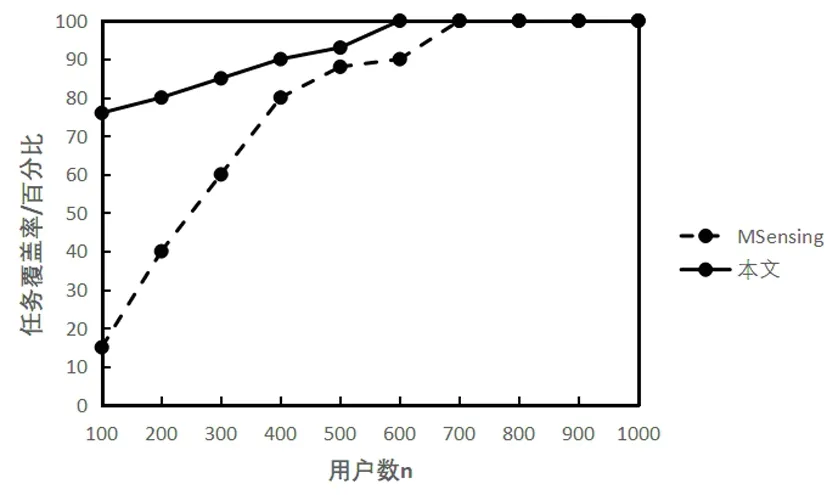
图5 (b)用户数与任务覆盖率

4 结 语

在针对用户参与感知任务中积极性不高导致任务分配率不足的问题，而提出了以用户为中心的逆向拍卖机制，最大化用户效用的同时保证了平台的效用。分别将竞拍过程分为赢标者候选和赢标者支付两个阶段进行，优胜者选择阶段过程中在多项式内解决了问题，支付报酬阶段则采取基于排序最高者的附加奖励方式，激发了用户参与积极性。实验结果则验证了此机制有效地提高了用户效用、平台效用和任务覆盖等指标，最终验证了该机制具有较好的激励效果。