基于局部一致性调整算法的犹豫模糊语言决策模型①
胡甜甜,金飞飞,曹 萌,张 莹,唐 玥
(安徽大学商学院,安徽 合肥 230601)
0 引 言
近年来决策领域的研究方法多,成果丰富[1-3]。在实际决策问题中,评估专家们通常对待评估方案的评价倾向于使用自然的语言来表达。Zadeh[4]提出的犹豫模糊语言方法(FLA)可以用来解决这一类定性的决策问题。Zhu等[5]提出的犹豫模糊语言偏好关系(HFLPRs)是在FLA方法上发展起来的有力工具,用于表达专家对一组备选方案两两比较的评价结果。目前,改进HFLPRs的一致性、构建决策模型是基于HFLPRs决策研究的热点问题。但很多关于一致性改进的研究还存在一些不足:Liu等[6]采用人为调整的方法,不仅效率低,且难以克服专家评价的主观性和不确定性;而Liu等[7]通过构建优化模型,虽然方法新颖,但过程复杂,计算繁琐。为提出一种简单高效的一致性改进过程、避免评价的主观性和可能存在的极端性,引用Wu等[8]的最小公倍数展开法则,同时限制语言变量在s1到s2τ-1之间,提出创新的一致性构造公式,结合迭代算法,构造了基于局部一致性调整算法的决策模型。
1 预备知识
语言变量以词语或句子等语言单位为变量[4]。一个备选方案所有语言变量就组成了语言术语集(Linguistic Term Sets, LTSs)。设S={s0,s1,…,s2τ}是一个LTS,则它满足以下条件[7]:
(1) 有序性:若sα,sβ∈S且α>β,则sα>sβ。
(2) 逆算子:neg(sα)=s2τ-α。
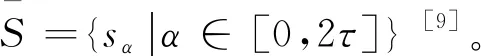
(1)sα⊕sβ=sβ⊕sα=sα+β;
(2)λsα=sλα;
(3)sα⊗sβ=sβ⊗sα=sα×β;

将语言变量sα的下标记为I(sα),即I(sα)=α。
定义1[11]假设h是一个具有#h个语言术语的HFLTS,则h的期望定义如式(1):
E(h)=sα
(1)
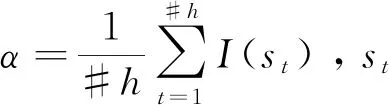
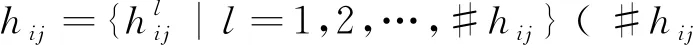
(2)
(3)

一般来说,在一个HFLPRH中,不同的hij,其LTS个数不一定相同。为了方便改进偏好关系的一致性,需保证同一个HFLPR中不同元素的语言术语个数相同。采用Wu等[8]提出的最小公倍数展开法则(LCMEP),具体定义见定义3:
定义3[8]设h={s1,s2,…,s#h}是基于LTSS具有#h个语言术语的HFLTS。则hr是一个具有r#h个语言术语的HFLTS,表达式为式(4):
(4)
h中的每一个语言术语sk在hr中都重复了r次。
2 乘性一致性改进算法
由于专家给出的原始的HFLPR不一定具有乘性一致性,因此提出新的局部一致性调整算法。此外,为保证算法的合理性和客观性,同时避免专家给出的语言术语过于极端,对于一个LTSS={s0,s1,…,s2τ},限制专家的评价在s1~s2τ-1之间。
2.1 HFLPR乘性一致性公式
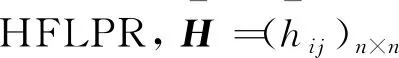
(5)
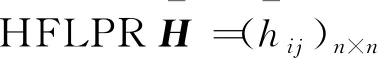
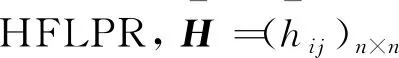
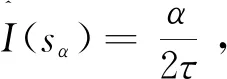
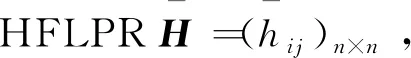
(6)
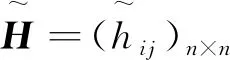
2.2 一致性指数(CI)
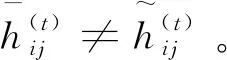
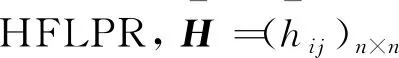
(7)

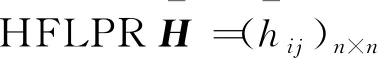
2.3 乘性一致性改进算法
算法1
输入 HFLPRH=(hij)n×n,阈值δ0、迭代参数θ。
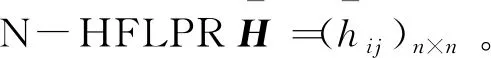
(8)
(9)
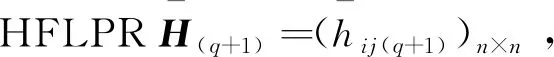
(10)
令q=q+1,返回步骤3。
Step 8 结束。

证明:由式(10)可知,对∀q,有
(11)
i,j∈(1,2,…,n),t=1,2,…,l
(12)
利用公式(9)知,对∀q,有:

(13)
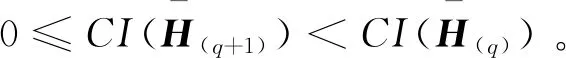
3 犹豫模糊语言决策模型及其应用
3.1 犹豫模糊语言决策模型的构建
对于一个HFL决策问题,假设有n个备选方案X={x1,x2,…,xn}。专家通过对方案两两比较,给出了初始HFLPRH=(hij)n×n。由初始的HFLPRH做出选择,可以利用以下决策模型:
算法2
输入:初始HFLPRH=(hij)n×n
输出:各方案的优劣排序

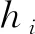
(14)
阶段C:根据定义5求出每个方案综合评价的期望,作为评价各方案优劣的标准。
3.2 案例分析
配送中心处于物流供应链的下游,能够满足客户多样化需求,是供应链中重要的物流节点。某物流公司准备拓展市场,扩大其物流网络覆盖面,除了需要在新区域布置终端节点,还需考虑建设一个配送中心,以方便集散货物,整合资源。由于新市场需求信息不完全,无法进行准确的定量分析,因而考虑用HFL方法。现有四个备选地址x1,x2,x3,x4。专家的偏好包含在LTSS中:S={s0,s1,s2,s3,s4,s5,s6,s7,s8}。记s0—特别差,s1—很差,s2—差,s3—稍微差,s4—相等,s5—稍微好,s6-好,s7—很好,s8—特别好。为了避免决策结果极端化,将专家的偏好限制在s1~s7。专家给出的初始HFLPR如式(15):
H=
(15)
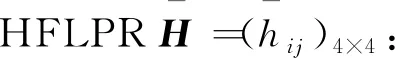
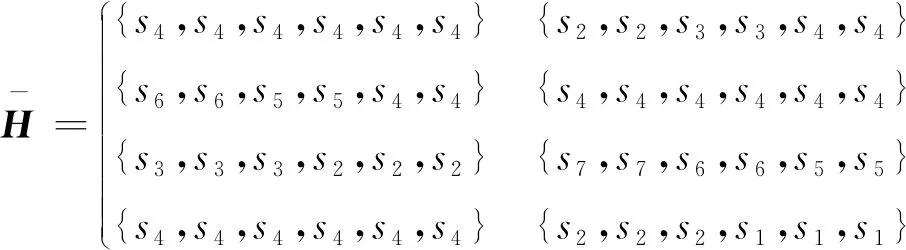
(16)
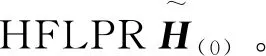
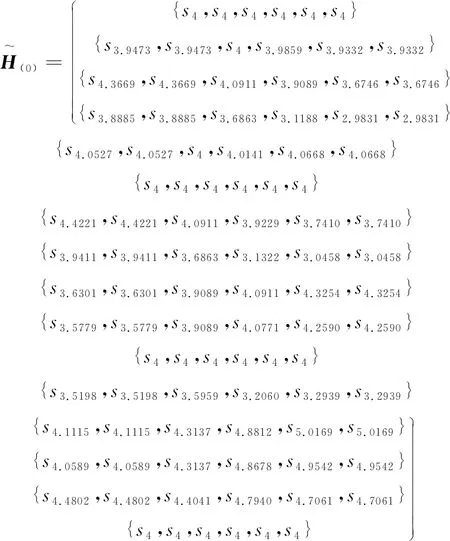
(17)

(18)
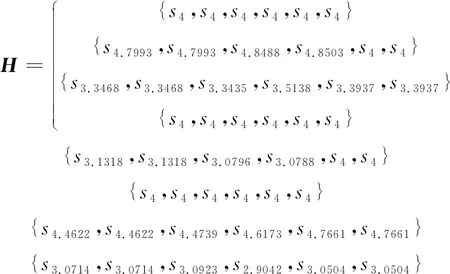

(19)
然后根据算法2,利用HLFA算子,得到:
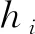
(21)
由此得出4个备选地址的排序结果:x2≻x3≻x1≻x4(这里'≻'表示为优于)。因此选择方案2,即在x2处建造配送中心。
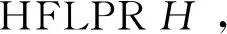
事实上,决策模型与文献[12]的区别主要在于初始HFLPR的规范化和一致性HFLPRs构造方法。首先融合了已有的LCME原则对原始HFLPR规范化,较好地保留了原始信息,使最终结果更贴近现实。设计的乘性一致性HFLPRs构造公式,虽然简单但运行效率较高,且结果合理,通过将公式运用于迭代算法中能有效解决犹豫模糊语言环境下的决策问题。
4 结 语
当决策缺少足够的信息且专家难以给出确切定量的评价时,可以考虑使用HFL方法辅助决策过程。为简单有效地处理此类决策问题,构建了一个基于局部一致性调整算法的HFL决策模型。首先给出了构造乘性一致性偏好关系的公式,设计了迭代算法以改进初始HFLPR的乘性一致性,给出了公式的限制条件以避免决策极端化。基于该算法,进一步构造决策模型,对满足可接受乘性一致性的HFLPRs,利用HFLA算子,计算得出各方案最终的评价值11。最终以配送中心选址算例证明该模型的合理性和实用性,分析了与其他方法相比的优势所在,丰富了HFLPRs及其乘性一致性的研究成果。
仅考虑了单个决策者的决策问题,而群决策能够有效降低决策的偶然性和主观性,使决策结果更加可靠,因此模型在群决策中的应用是重要的发展方向,此外,在集成HFLPRs的信息时采用的是最常见的HFLA算子,未来可以考虑使用其他更加有效的集成算子,进一步提高模型的准确性。

