高层住宅落地式脚手架附墙安全支撑施工技术研究

落地式脚手架是可以直接固定在地面上的架型结构主体，其作为重要的工程施工保障平台，与其它承压式结构相比，具有相对较强的荷载变异性。按照所属搭建位置的不同，落地式脚手架可分为里脚手架、外脚手架两大类；按照构造形式的不同，则可分为爬式脚手架、立杆式脚手架、挑式脚手架、桥式脚手架、悬吊式脚手架、门式脚手架等多种类型[1]-[2]。在保持附墙支撑的施工状态下，落地式脚手架的扣件连接节点一般采用半刚性元件结构，且节点刚性能力实际数值受到安装质量、扣件质量等多个条件的限制，在实际操作过程中，刚性节点的支撑性能也存在较大差异。

国内关于落地脚手架结构的研究起源于上世纪60年代，而以英、日、法为代表的其他国家在上世纪70年代前后就已经制定出了完整的脚手架应用标准。他们认为，这种架式形态结构满足“单元集合”的力学承载条件，可通过计算复支撑力学指标的方式，然而传统扣件式钢管脚手架对高层住宅复杂形体结构的适应能力有限，很难实现对附着升降架体的稳定支撑。为解决此类问题，本文对附着受力进行分析实验，改进高层住宅落地式脚手架附墙安全支撑施工技术方案，并通过对比实验的方式，分析落地式脚手架支撑性能。

1.高层住宅脚手架静力、动力特性分析

高层住宅脚手架的静力及动力特性条件由支撑载荷、振动方程、有限元边界条件三部分组成，具体分析计算方法如下：

1.1 支撑载荷

为实现落地式脚手架的安全性附墙支撑，附着架体立杆间的纵向距离不得超过1.5m、横向距离不得超过1.05m，相邻纵杆、横杆间的步距实值也必须小于1.5m。按照实际层高高度来计数，连墙杆竖直间距水平需要保持在4.5m-5.0m之间，也就是常说的“每层三跨”施工技术。按照高层住宅的形体结构进行设置，为保证附墙安全施工的有效性，首排脚手架立杆的实际位置必须低于落地支撑线，整个底部立杆则采取不同长度钢管参差布置的搭建方式，利用钢管立杆间的接头交错布置原理，使相邻横杆间的高度方向相互错开达到500mm，且要求同一区域内的架体接头必须处于不同跨度分区环境中[3]-[4]。

设ξ代表架体立杆间的纵向距离实值，α代表架体立杆间的横向距离实值代表底部钢管的长度平均值，联立上述物理量，可将地式脚手架的支撑载荷量表示为：

1.2 振动方程

与支撑载荷及其他静力有限元条件一样，架体振动方程建立必须选取固定的单元位移模式，也就是在脚手架外测立面的首端和尾端各设置一道独立的剪刀撑结构。为获取最大化的附墙稳定性支撑系数，该结构必须由架体底部延续至顶部单元。出于安全性考虑，相邻两道竖直剪刀撑之间的净距离数值不得大于15m。通常情况下，剪刀撑斜杆宜采用搭接的连接形式，相距1m的架体之间至少应保留2个旋转扣件，以实现脚手架与墙体之间的固定性支撑[5]。在脚手架负重的情况下，剪刀撑斜杆会出现一定程度地振动趋势，为避免附墙安全性支撑能力的下降，旋转扣件的固定位置必须保持在横向水平杆伸出端之上，而扣件中心线与脚手架主节点间的实值距离则不宜超过150mm。在搭设首层脚手架时，应沿架体四周设置多个斜支撑结构，除拐角点保持双向谐振形态外，其余各支撑节点均处于单向谐振形态，以便后续施工性拆除的直接实施。设 k代表剪刀撑结构实际设置数量，δ代表脚手架旋转扣件所具备的固定性支撑动量，联立公式（1），可将高层住宅脚手架的动力学振动方程表示为：

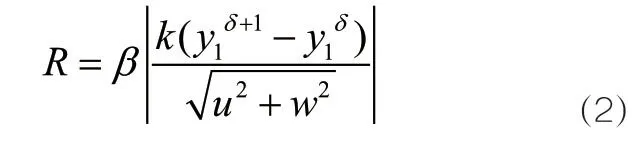
其中，y1代表尾端剪刀撑结构的延续性支撑系数，y0代表首端剪刀撑结构的延续性支撑系数，u代表脚手架横向水平杆的振动连接条件，w代表脚手架纵向竖直杆的振动连接条件。

1.3 有限元边界条件

从参考落地式脚手架的节点分布情况（图1）来看，分析附墙安全支撑施工的有限元边界条件，需要以架体静力特性原理及振动方程作为研究前提。一方面可防止振动连杆的不当滑动；另一方面也可降低架体底部支撑载荷量的扩张速率[6]。

设f代表与附墙撑力指标相关的线性分布条件，代表单位时间内元件中的压力承载变化量，联立公式（2），可将落地式脚手架支撑施工有限元边界条件定义为：

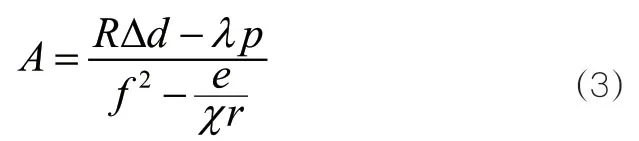
其中，λ代表架体所具备的线性承力系数，p代表施工变力的线性支撑负载量，e、r分布代表两个不同的附墙稳定性支撑力学指标，x代表安全性架体支撑附墙条件。

2.落地式脚手架附墙安全支撑施工方案

在高层住宅脚手架静力、动力特性原理的支持下，按照架体结构、附着支撑子系统的搭建流程，完成新型附墙安全支撑施工技术方案设计。

出于安全性施工能力的考虑，高层住宅落地式脚手架（图2）的架体结构平均搭建高度的设定参考建筑物标准层的实际层高，除个别架体结构外，架体纵向高度一般保持为50m，大多为8个小型步架外加1个大型单排架的物理结构，相邻架杆之间的纵向距离处于1.8m-2.0m之间，而横向宽度却始终保持为1.0m左右[7]-[8]。两个竖直立杆间的最大水平间距不得超过1.5m，且机位的横向跨度也必须小于6.0m，高层住宅的安全性支撑施工准则规定：附墙支承跨度与架体全高间的乘积应小于110m，而单体支撑梁的长度则完全取决于水平支承跨度及架体悬挑长度，大部分情况下，处于5m-9m之间。

落地式脚手架承载力是稳定控制的，非线性屈曲分析可以考虑结构的几何非线性、材料非线性、初始缺陷和残余应力等因素[9]-[10]，可以真实反映结构的实际情况。

图1 脚手架部分节点图

图2 高层住宅落地式脚手架结构图

图3 高层住宅脚手架施工现场

非线性屈曲的方程表达式如下：

其中，KT表示结构总切线刚度矩阵，KT=KL+KN+KS,KL、KN、KS分别表示结构的线性刚度矩阵、大变形矩阵和总应力矩阵，δ、P分别表示总位移列阵和总荷载列阵。

采用线性屈曲分析可以预测屈曲荷载的上限。线性屈曲的分析是假设结构在受载变形过程中，无结构形状的变化，而当屈曲发生时，结构构形才会突然跳到另一个平衡位置，其屈曲判断准则为：

即：

式中，K0为初始刚度矩阵，K0=ʃ BTDBdV，KG表示几何刚度矩阵为屈曲特征值N分别为建立在结构初始构形上的应变矩阵、弹性矩阵、应力矩阵、形函数矩阵。Pcr、P分别为屈曲的临界荷载、设计的使用荷载。

在线性屈曲分析中，假定结构失稳时仍处于弹性小变形范围内，结构的内力与外荷载呈正比。

3.实用施工检测方案

为验证落地式附墙脚手架的实际应用价值，设计如下对比实验（图3）。选取一处于施工状态的高层住宅作为实验监测对象，在等高楼体两侧分别搭建新型落地式附墙脚手架和传统扣件式脚手架，其中前者作为实验组，后者作为对照组。在相同实验环境下，不断增加外界作用力的数值水平，记录TSC、LSC支撑系数的具体变化情况。

借助数据记录仪分析实验组、对照组脚手架的横向与纵向施工参量，在既定实验时长内，将两组记录数据同时输入检测分析主机中，研究相关指标参量的实际变化趋势。

TSC系数、LSC系数都能够直接反应附着落地脚手架的支撑稳定性，通常情况下，参数指标的实值水平越高，脚手架的稳定性能力越强，反之则越弱。

表1反应了50min的实验时间内，实验组、对照组TSC系数的具体数值水平。

分析表1可知，对照组TSC系数的实值波动能力相对较强，去除最大数值3.92、最小数值3.69，可知对照组TSC系数的剩余极大值为3.91、剩余极小值为3.74，二者差值为0.17。实验组TSC系数的实值波动能力相对较弱，去除最大数值5.15、最小数值5.11，二者差值仅为0.04，远低于对照组的极限数据差值水平。从极大值角度来看，实验组的5.15与对照组的3.92相比，上升了1.23；从极小值角度来看，实验组的5.11与对照组的3.69相比，上升了1.42。综上可知，应用落地式附墙脚手架后，TSC系数出现了明显增大的变化趋势，确实增强了附着架体结构的支撑稳定性，实现了对高层住宅复杂形体结构的有效适应。

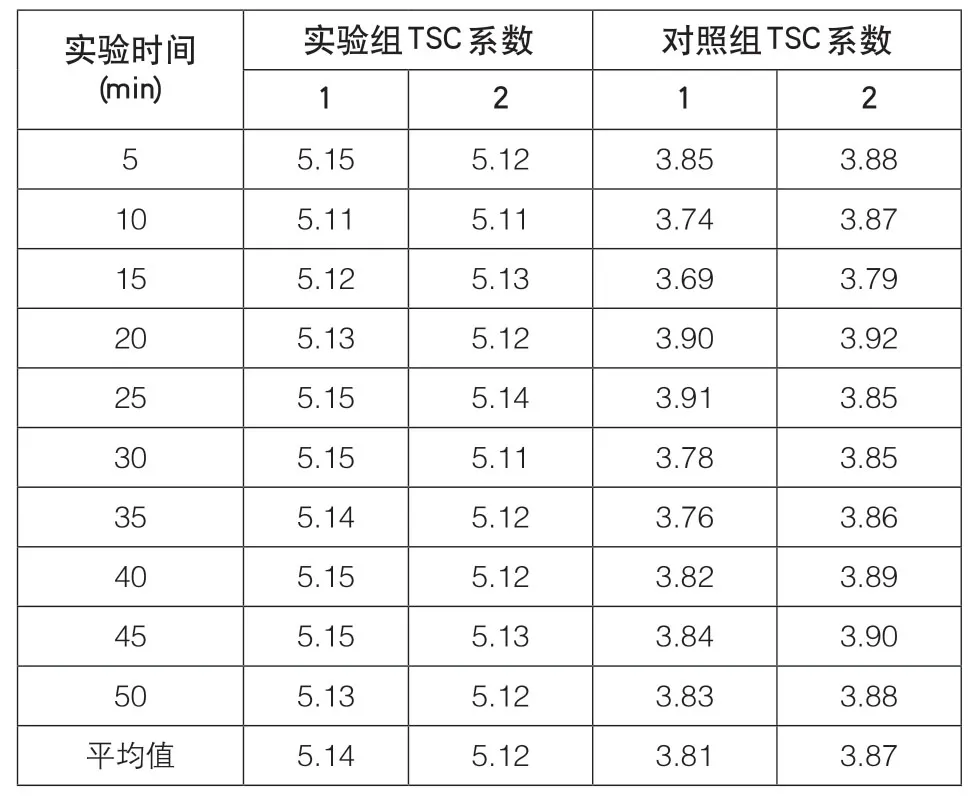
表1 TSC系数对比表

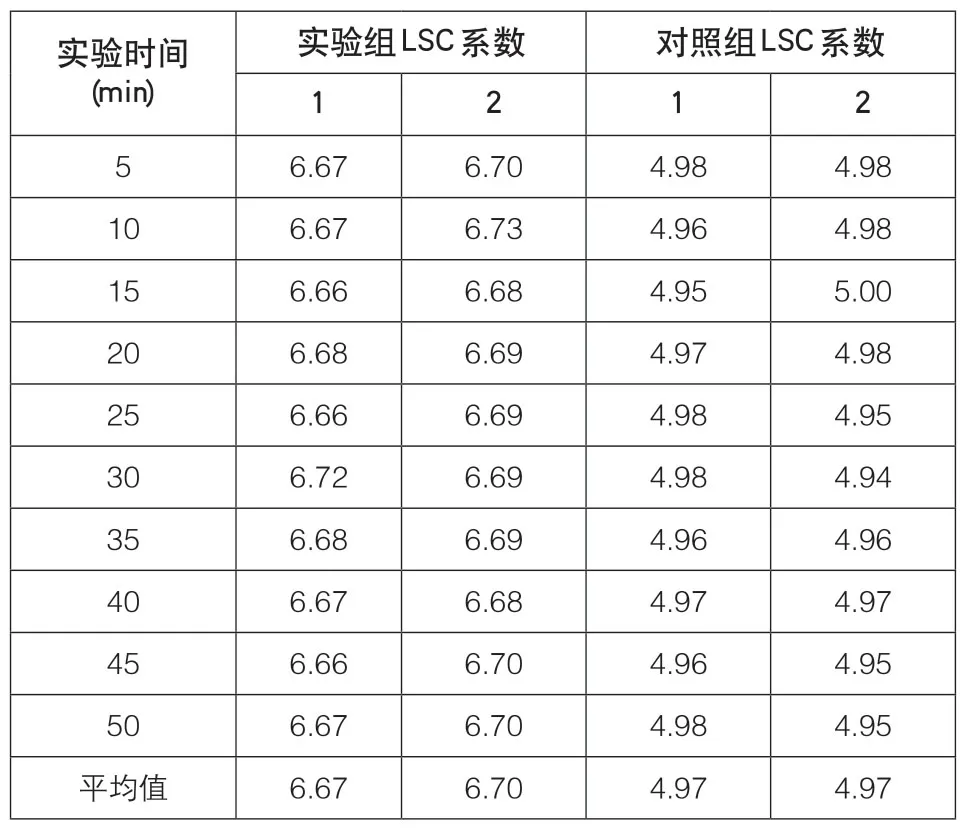
表2 LSC系数对比表

表2反应了50min的实验时间内，实验组、对照组LSC系数的具体数值水平。

分析表2可知，对照组LSC系数的实值波动能力相对较弱，去除最大数值5.00、最小数值4.94，可知对照组TSC系数的剩余极大值为4.98、剩余极小值为4.95，二者差值仅为0.03。实验组LSC系数的实值波动能力相对较强，去除最大数值6.73、最小数值6.66，二者差值为0.07，虽高于对照组的极限数据差值水平，但二者间差值距离不足0.10，基本可以忽略不计。从极大值角度来看，实验组的6.73与对照组的5.00相比，上升了1.73；从极小值角度来看，实验组的6.66与对照组的4.94相比，上升了1.72。综上可知，应用落地式附墙脚手架后，LSC系数也出现了明显增大的变化趋势，增强了附着架体结构的支撑稳定性，实现了对高层住宅复杂形体结构有效适应的实用需求。

图4 风速传感器安装示意图

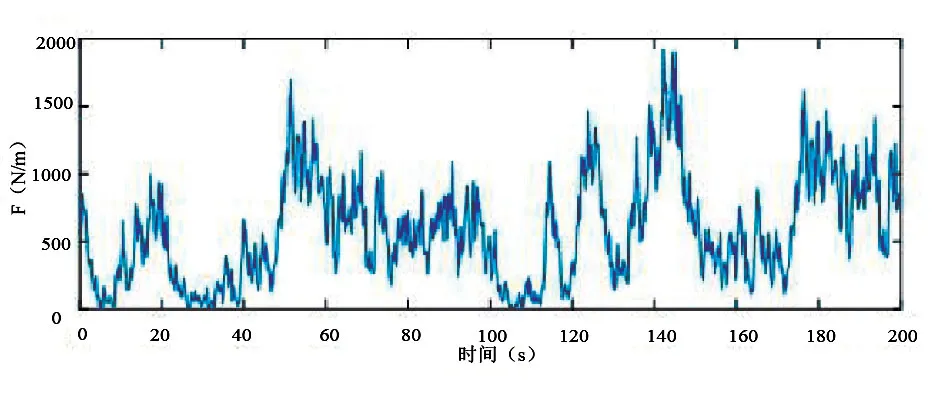
图5 荷载时程曲线图

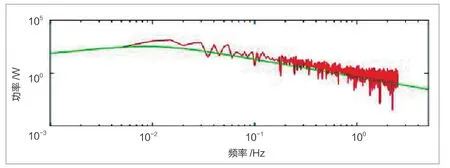
图6 模拟功率谱与目标谱的对比曲线图

风荷载监测以风速为监测指标，采用WinS．YX．FG．05V风速传感器，风速传感器安装在附着式升降脚手架顶部，尽量避开塔吊起吊碰撞K域，采用螺栓固定牟固，防止使用过程中发生脱落，其安装示意图如图4所示。

表3 脚手架风荷载体型系数

风荷载标准值ωk的计算公式如下：

上式中，k表示风压的折减系数，在取当地基本风压时，取值为0.7；µs表示脚手架的风荷载体型系数；µz表示风压高度变化系数；ω0表示基本风压，架体升降状况时可以取值为0.25kN/m2。

由图5可以看出，通过对风荷载进行检测，可得出风荷载曲线，从而根据体型系数（表3）与《建筑结构荷载规范》进行调整，增强脚手架施工稳定性。

为进一步验证支撑稳定性，采用Matlab编制响应程序，即可得到迎风面不同标高处的模拟功率谱与目标谱的对比曲线（图6）。

从图6可以看出，绿色表示目标曲线，红色表示功率曲线。功率曲线与目标曲线之间拟合程度较高，证明功率满足目标要求。主要原因在于本文支撑技术从附着支撑子系统方向着手，实现对框架主体的控制与支撑，完成高层住宅落地式脚手架附墙安全支撑施工技术方案设计，提高支撑稳定性。

4.结语

落地式附墙脚手架完善了附着支撑子系统结构主体，又重新计算了支撑载荷的实际数值水平，通过架体振动方程的建立，确定必要的有限元边界条件，实现了对高层住宅脚手架静力及动力特性的分析研究。从实用性角度来看，TSC系数、LSC系数的同步上升，不仅解决了架体结构对高层住宅复杂形体结构适应性较弱的问题，也适当增强了脚手架主体结构的支撑稳定性，符合推广与应用的实际施工需求。