农房不动产测量中无人机倾斜摄影测量技术的应用分析
王凯伦
(河南智联时空信息科技有限公司,河南 郑州 450003)
1 引言
倾斜摄影测量技术是近年来测绘领域快速发展的一项高新技术,通过无人机平台搭载多角度组合传感器采集影像数据,弥补了传统摄影测量仅从垂直角度采集数据的局限。以无人机倾斜摄影测量技术为基础生产的数字表面模型可从三维方面提取空间地理信息,速度快、精度高、三维真实感强。从无人机的选型、系统集成、航线规划等方面出发[1-2],无人机倾斜摄影测量技术在大比例尺地形图测量中的应用已较为成熟[3-6],但针对农房不动产测量的应用仍需深入研究。
本文从无人机倾斜摄影测量技术设备选型、航测设计、矢量采集和精度验证等方面进行分析,结合实例对无人机倾斜摄影测量技术生产的数据精度进行了验证,并对该技术应用中存在的问题进行分析,为倾斜摄影测量在农房不动产测量中的应用提供参考。
2 作业方法
2.1 无人机航测数据采集
无人机航测数据采集主要影响因素有无人机平台、任务荷载系统、航线布设和像控点布设。
(1)测绘项目常用的无人机平台有固定翼无人机、多旋翼无人机、垂直起降固定翼无人机。农房不动产项目对测量精度、稳定性等因素要求较高,一般选用多旋翼无人机和垂直起降固定翼无人机。
(2)任务荷载系统是无人机倾斜摄影测量的核心部分,主要包括多角度多镜头的倾斜摄影相机、云台、同步控制装置、姿态与位置采集系统等[1]。倾斜摄影相机常用的有五镜头组合相机、三镜头组合相机。
(3)根据测区的地理概况,设计航向重叠度、旁向重叠度、相对航高等参数,规划航线。
(4)像控点布设是影响倾斜摄影测量绝对坐标精度的主要因素,需尽可能地覆盖到全部区域。
2.2 数字表面模型构建和模型精度检查
基于无人机航测数据采集的影像,利用倾斜摄影建模软件进行处理,在影像数据输入完成后,通过几何校正、区域网联合平差、影像密集匹配、特征点云生产、TIN 构建、纹理映射,完成数字表面模型的生产工作,并利用冗余像控点对模型精度进行检核。
2.3 矢量数据采集
以数字表面模型为基础,对建、构筑物进行矢量数据采集。
2.4 矢量数据精度检查
采用GNSS-RTK、全站仪、钢卷尺结合的方法对矢量数据进行精度检核,检核主要包括两方面:(1)基于GNSS-RTK 和全站仪测量建、构筑物的特征点作为检核点,对矢量数据的特征点精度进行检核;(2)利用经检校的钢卷尺测量建、构筑物的边长作为检查边长。
矢量数据的精度需满足表1 和公式(1)的要求[7],超出限差的数值作为粗差值,粗差值不参与中误差计算,粗差率不得高于5%,否则视为不合格[8]。

限差/m 误差/m 备注±0.10 ±0.05 用于农村新型社区房屋测量±0.20 ±0.10 用于宅基地和集体建设用地上房屋测量

公式(1)中,mj是相应等级房角点的点位中误差(单位:m);D是相邻房角点间的距离(单位:m);ΔD是房角点坐标计算的边长与实量边长较差的限差(单位:m)。
3 应用分析
3.1 测区地理概况
本次实验选择的应用测区为某行政村,地面起伏小,行政区划面积约2.92 km2,居民地面积约为0.36 km2,建、构筑物分布较为集中。
3.2 航测规划方案
无人机平台采用大疆M600,任务荷载系统采用红鹏AP3400R。航测规划方案如表2 所示。测区航测采集共拍摄照片11777 张,理论地面分辨率为0.01 m。

项目 参数相对航高(m) 83焦距(mm) 35传感器尺寸(mm) 23.5×15.6航向重叠度 ≥80%旁向重叠度 ≥80%航速(m/s) 5
3.3 数字表面模型建立和模型精度检查
航测外业采集完成后,采用倾斜摄影建模软件制作数字表面模型,如图1 所示。

图1 数字表面模型
数字表面模型完成后,通过特征点检核模型精度,检核结果如表3 所示。最小误差值为1.2 cm,最大误差值为3.6 cm,中误差为2.5 cm,数字表面模型精度满足表1 要求。

检测点号 X 检(m) Y 检(m) X 图(m) Y 图(m) ΔS(cm)1 3742121.929 512083.424 3742121.926 512083.412 1.2 2 3740684.624 513437.471 3740684.607 513437.472 1.7 3 3742139.415 512059.961 3742139.4 512059.966 1.6 4 3741475.845 512614.97 3741475.846 512614.992 2.2 5 3742117.546 512077.524 3742117.554 512077.499 2.6 6 3741495.676 512595.421 3741495.704 512595.417 2.8 7 3740644.313 513421.292 3740644.305 513421.324 3.3 8 3742131.721 512974.182 3742131.685 512974.181 3.6
3.4 矢量数据采集
基于数字表面模型,利用三维测图软件采集矢量数据,如图2 所示。

图2 矢量数据采集
3.5 矢量数据精度检核和基于数字表面模型的误差分析
3.5.1 特征点精度检核
房角点精度检核即对矢量数据的绝对精度检核。检核点共143 个,均为房角点、围墙点等建、构筑物特征点。根据检核点测量方法,中误差计算公式为[9]:

公式(2)中:m中是中误差,n是检核点个数,Δ是点位误差值。
图3 和图4 分别为检核点X值差值区间和Y值差值区间点位数量分布图,在143 个检核点位中,X值在-5 ~+5 cm 范围内的占总数的93%,Y值在-5 ~+5 cm占总数的80%,小误差出现的概率较大,X值、Y值中误差呈正态分布,符合偶然误差分布规律。此次检核点数据具有代表性,可作为分析研究依据。图5 为检核点与矢量数据同名地物点点位误差统计图。


测区矢量数据共143 个检核点,其中,142 个检核点误差在0 ~20 cm 间,满足限差要求;1 个检核点误差超出20 cm,不满足要求,为粗差点,粗差率为0.6%,剔除该点后,最大误差绝对值为14.0 cm,最小误差绝对值为0.2 cm,根据公式(2)计算可得,中误差为4.95 cm。矢量数据特征点精度满足表1 及粗差率要求。

图5 检核点与矢量数据同名地物点点位误差值统计
3.5.2 基于数字表面模型特征点误差分析
图6 至图8 为特征点精度检核中误差大于10 cm的点位,为探索矢量数据部分区域特征点误差较大的原因,以数字表面模型为基础进行比对,结果如下:
(1)图6 检核点处矢量数据与模型贴合精度较好,但与检查值误差较大,差值为14 cm。建筑物纹理较好,但数字表面模型精度偏低。由此得出,无人机航测时受光线、风速等因素影响,未能精确获取部分建、构筑物的位置与姿态数据,导致数字表面模型精度降低。 (2)图7 和图8 的检核点处误差较大,差值分别为10.4 cm、11.2 cm。结合数字表面模型逐点查询,图7处是两家交界处,有互相遮挡情况,模型纹理较差;图8 处是围墙与房屋交界处,模型纹理较差。由此得出,宽度较窄的线状地物、纹理较差区域和遮挡区域是基于数字表面模型采集的矢量数据的精度薄弱点。

图6 检核点点位精度(红圈为矢量点,绿圈为检核点)

图7 检核点点位精度(红圈为矢量点,绿圈为检核点)

图8 检核点点位精度(红圈为矢量点,绿圈为检核点)
3.5.3 房屋边长精度检核
房屋边长精度检核为矢量数据的相对精度检核。从测区房屋中随机抽取94 个房屋边长作为检核边长。房屋边长的误差分布较为集中在0 ~10 cm 间(如图9所示),呈正态分布,符合偶然误差分布规律,可作为分析研究依据。将检核边长与矢量数据同处边长进行对比,差值统计如图10 所示。


图10 检核边长与矢量数据同处边长差值统计
通过公式(1)计算,在94 条检核边长中,2 条差值超限,92 条满足精度要求,粗差率为2.1%。在限差范围内,最大误差绝对值为0.10 m,最小误差绝对值为0.00 m,中误差为0.05 m,矢量数据房屋边长的精度满足公式(1)及粗差率要求。
3.5.4 基于数字表面模型房屋边长的误差分析
图11 和图12 为房屋边长超限区,为研究房屋边长超限原因,基于数字表面模型进行比对,结果如下: (1)图11 宗地主房长边由于树木遮挡,数字表面模型局部缺失或模糊,采集时难以确定精确值,导致矢量数据精度较低。由此可得,树木遮挡导致影像难以精确获取是影响房屋边长矢量数据精度的重要因素。 (2)图12 宗地主房长边因为房屋年代久远,墙面砖缝纹理较差,无人机难以获取精确照片。由此可得,建、构筑物纹理无规律且难以获取,是影响模型精度和矢量数据精度的重要因素。
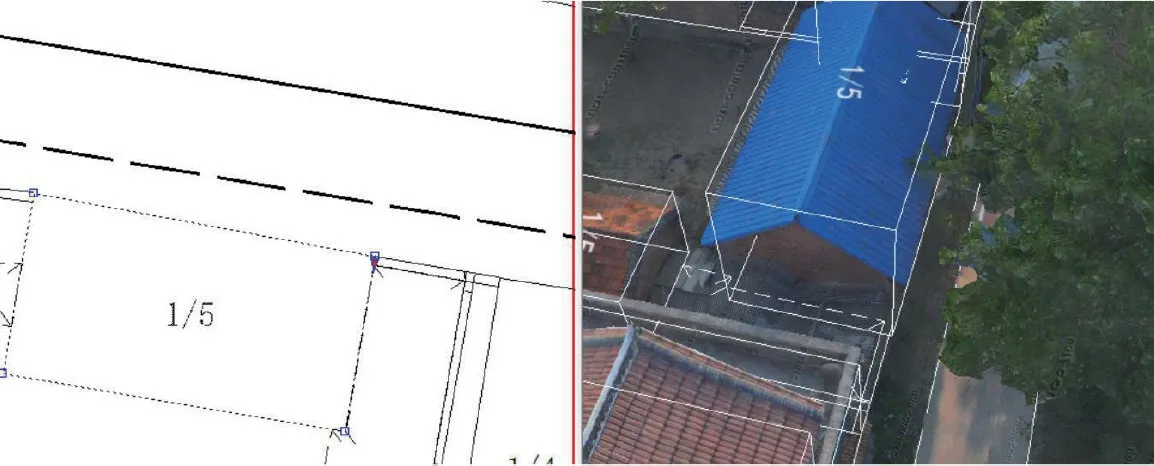
图11 主房长边受遮挡严重

图12 主房房屋年代较长
4 结论
综上研究,本文得出结论:(1)无人机倾斜摄影测量技术在理论基础、作业方法和精度检核等方面,均能满足农房不动产测量要求。(2)以应用测区为基础,对无人机倾斜摄影测量的矢量数据精度进行了检验,矢量数据特征点中误差为4.95 cm,房屋边长的中误差为0.05 m,且测量粗差率均低于5%,符合农房不动产测量精度的要求。(3)基于应用测区精度检核数据,逐项分析了无人机倾斜摄影测量技术应用中的问题,为该技术应用于农房不动产测量提供借鉴。

