基于动态约束分析的舰载机着舰复飞技术研究

冯玉博, 姚明智，李 冬, 张 伟, 欧阳文恒

(1. 92728部队, 上海 200436;2. 91899部队, 辽宁 葫芦岛 125001;3. 海装沈阳局驻沈阳地区第一军事代表室, 沈阳 110000;4. 海军装备部驻九江地区军事代表室，江西 九江 332000)

舰载机以其特殊的作战平台和起降方式, 与陆基飞机相比, 具有更加苛刻的要求。研究表明, 舰载机在航母上降落是其发生事故最多的环节。为了提高舰载机的生存率,通过舰载机飞行仿真模拟和飞行试验方式两种手段，对舰载机逃逸复飞技术进行研究。飞行仿真技术以其费用低、无危险性以及能够模拟许多训练中不易出现的场景, 备受研究人员的关注。建立精确的舰载机飞/发一体化控制模型，模拟舰载机所处的各种环境和运动, 对其着陆复飞情况进行分析, 可以为提高舰载机逃逸成功率提供参考和借鉴。

国外对这方面技术研究的较多, 但都涉及到一定的军事机密, 没有太多具体的研究资料, 但从目前公开的相关资料看来, 国外对舰载机逃逸能力研究非常重视, 并且研究的很深入。在国内, 虽然我国的航母和舰载机起步较晚, 但发展很快, 取得了一系列瞩目的成绩。 一直以来, 工业部门及院校对舰载机技术做了大量的研究工作。通过模拟仿真的技术手段对舰载机逃逸性能进行研究, 主要考虑甲板风和航母在海面上运动两个关键因素, 以此为基础建立舰载机飞行运动模型。全机模型分为机身、起落架数学模型两部分，其形式是微分方程、传递函数或状态空间表达式[1-2]。为了能够成功安全逃逸，舰载机发动机也要有很好的加速性能，才能在有限的甲板空间让舰载机尽快达到所需起飞速度。在模拟中加入精确的发动机控制模型, 并且对发动机加速控制规律优化设计; 按照基于飞/发一体化约束的飞机设计思路[3-4], 建立结合舰载机自身特点并考虑发动机推力因素的飞机逃逸运动模型进行研究。提高舰载机的逃逸性能, 要设计出最优的发动机加速控制规律[5-6]。从上世纪至今, 研究人员已对过渡态控制规律优化设计开展了大量的研究工作。在成熟的非线性优化控制理论基础上，利用线性规划、非线性规划以及相似理论等技术手段，实现加速控制规律的优化设计[7]。但上述研究建立的模型相对粗糙, 少有考虑地面效应的影响, 对于发动机加速规律研究的不够深入, 没有充分发掘发动机的潜力。本文正是在上述研究的基础上, 解决上述问题, 基于涡扇发动机部件模型和飞机气动模型, 依据能量法建立飞/发一体化控制模型, 作为舰载机复飞技术研究的基础。模型充分考虑了着陆时的升阻特性、地面效应和飞机着舰重量等因素，采用功率提取法改进涡扇发动机加速控制规律和供油规律, 最大限度地挖掘发动机的工作潜力，并与原控制规律进行比较分析。

1 飞/发一体化控制模型

1.1 发动机动态模型

建立舰载机飞/发一体化控制模型, 是研究舰载机复飞的基础。首先建立发动机动态模型, 动态模型是在发动机稳态模型基础上建立的。在建立动态模型时, 考虑了发动机的容积效应。此时, 转子动态平衡方程变为:

(1)

式中：WT,WC为涡轮、压气机的质量流量,ΔhT,ΔhC为涡轮、压气机焓值变化量,n为转速,Padd为额外功率。

动态流量连续方程：

(2)

动态能量方程：

(3)

在给定加减速控制规律下，上述微分方程中的所有微分项均采用隐式欧拉格式差商求解。

1.2 飞机/发动机一体化控制模型

舰载机的性能既取决于飞机主要设计参数，又取决于发动机性能，这就要求飞机和小涵道比涡扇发动机设计参数互相匹配。首先建立飞机的受力分析模型, 如图1所示。

图1 飞机受力分析

如图1所示, 如果把飞机作为一个运动质点来看, 假设安装推力和气动阻力作用在与飞行速度同一个方向上, 对图1的飞机进行受力分析后, 运用能量法得到以起飞推力载荷TSL/GTO和机翼载荷GTO/S表达的式子, 见式(4)。

(4)

式中：T是发动机安装推力,D是带正常外挂物的飞机阻力,R是由起落架、非正常外挂物或阻力伞等这些突出部分引起的附加阻力之和,V是飞行速度,G是飞行器重量,dh/dt是飞机的高度变化率,g是重力加速率。

为了便于后续的分析和计算, 得到式(4)的无因次化形式。

(5)

式中：ze=h+V2/2g为飞机的瞬时势能和动能之和，常被称为“能量高度”，进一步得到:

(6)

式中：α表示最大油门状态下的发动机安装推力变化率，TSL表示海平面发动机安装推力，β为着舰重量比，取决于飞机已经消耗掉多少燃油和投放掉多少有效载荷，GTO表示飞机最大起飞重量。经过一系列推导, 得到评估飞机和发动机关系的表达式[8]。

(7)

式(7)表示飞机在任务剖面上的每一点都成立, 由式(7)可以看出, 飞机的翼载和推力载荷存在一定的关系。

舰载机着舰过程中, 处在复杂的气流环境下, 除自然风场外, 还存在着在舰尾处下沉又经海面反射形成的“公鸡尾”稳态舰尾流, 舰岛后方以及排放烟气流形成的紊流,等, 这些都对着舰形成干扰。舰载机在着舰过程中，地面效应对近地飞行时飞机的迎角、升力、阻力和洗流场都有明显影响, 而尤以升力效应对起飞特性的影响最为明显[9]。舰载机在飞离甲板瞬间地效升力突然损失, 其升阻关系必然变化, 在舰载机复飞时需要对这一现象加以考虑, 这些问题在飞/发一体化控制模型都做了修正。图2给出舰载机在考虑地面效应后的升力系数变化量ΔCL随高度h的变化关系。

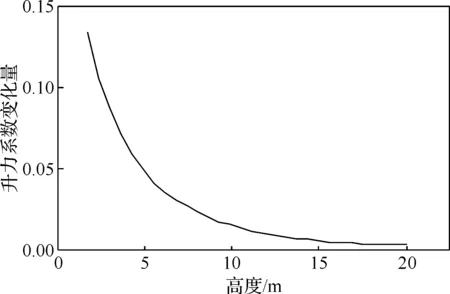
图2 舰载机在考虑地面效应后的升力系数变化量随高度的变化

由图2可以看出, 当h=9.0 m时, 地效引起的ΔCL可以忽略不计。

2 舰载机着舰复飞典型航段评估分析

在评估分析各航段前, 首先给出飞机飞行的典型任务剖面, 如图3所示。在各航段提出明确的技术指标基础上, 结合式(6)和式(7)就可以得到航段具体评估式, 作为分析评估的基础。

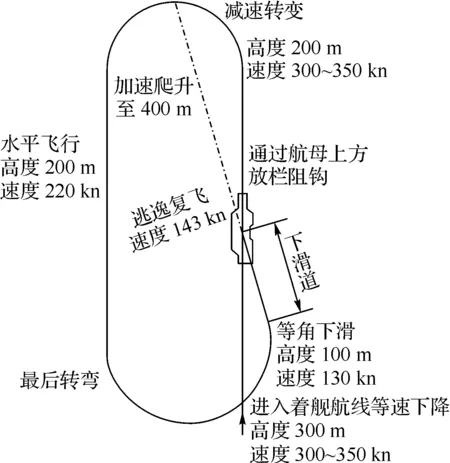
图3 舰载机着陆过程典型剖面

着舰复飞过程包括7个阶段, 分别为等速下降、减速转弯、水平飞行、最后转弯、最后进场时等角下滑、触舰滑跑、加速爬升。各个阶段满足在特定条件下形如式(7)的约束关系，求解约束关系式。

3 发动机加减速控制规律研究

舰载机在复飞阶段, 发动机的加速起到了关键的作用。以往的控制规律没有最大限度地挖掘发动机的最大潜能。这里采用功率提取法模型的加减速控制规律[18]。

以单轴涡喷发动机为例, 在换算转速保持不变时, 要使发动机稳态工作点偏离正常的稳态工作点有两种方法: 一是改变尾喷管喉部面积A8,二是在转子上提取额外功率Padd。如图4所示,A8减小以及Padd增加时, 发动机稳态工作点向喘振边界靠近, 正好与加速过程的工作点的位置一致, 而A8增加以及Padd减小时, 稳态工作点则远离喘振边界, 正好与减速过程的工作点的位置一致。

图4 A8和Padd对发动机稳态点的影响

对于双轴涡扇发动机，改变A8可能不能改变高压压气机工作点，还可能会导致风扇工作点比压气机工作点更早地进入喘振边界，而加速控制规律一般是以高压压气机工作点为基础来设计的, 这样发动机就进入喘振。功率提取法则可以保证涡轮工作点与加、减速过程中基本一致，所获得的Padd也非常接近加、减速过程的涡轮剩余功率。功率提取法应用于双轴涡扇发动机时，直接从高压转子提取，如果要保证风扇工作点位置，也可以同时在低压转子上提取。

当Padd=0时, 对应发动机正常的稳态工作点A; 当Padd>0时, 涡轮功率大于压气机功率, 需要的燃烧室供油量比正常时高, 对应工作点B; 当Padd<0时, 涡轮功率小于压气机功率，需要的燃烧室供油量比正常工作时低，故对应工作点C。当Padd≠0时，在慢车状态到最大状态之间若干个换算转速下，通过改变Padd，获得的若干个A点和若干个B点, 这些“加速线”和“减速线”对应的即是发动机的加、减速控制规律。

随着Padd的增加, 稳态工作点(相当于换算转速下的加速工作点)逐渐靠近喘振边界,在满足喘振裕度限制、高压涡轮进口温度限制以及燃烧室余气系数限制的条件下, 尽可能增加Padd，直至获得允许的Padd最大值, 获得的这些工作点的供油规律即为最优加速控制规律。在任意转速下的高压转子加速功率和角加速度均为最大值, 总的加速时间tacc最短。

(8)

式中:Ip为发动机转子转动惯量,nidle为慢车转速，nmax为最大状态转速。减速控制规律也是类似分析的。

采用定喘振裕度的功率提取法设计控制规律，对于双轴混排发动机，压气机进口导叶和喷管面积一般可调, 为高压转子换算转速的函数，只有尾喷管面积是独立变化的，其作用为保证低压转子的转速按照设计的规律变化。此时整个发动机有两个独立的调节变量，即尾喷管喉部面积A8和燃烧室燃油流量Wfb。事先给定节流过程的A8变化规律。在这种情况下，舰载变几何发动机的功率提取法按定几何发动机的功率提取法来获得。当给定喘振裕度和发动机转速的情况下时，可由压气机喘振裕度直接求出增压比，获得高压压气机进口换算流量。假设燃烧室后总温和风扇增压比，可以获得风扇、高压压气机和燃烧室所有的计算参数，再将燃烧室出口燃气流量直接换算并假设为高压涡轮进口换算流量，那么对于高压涡轮而言，通过进口换算流量和换算转速，可以获得高压涡轮出口全部参数。同理将高压涡轮出口燃气流量换算成低压压气机进口换算流量，在已知进口换算转速的条件下，获得低压涡轮出口所有参数。此时双轴混排涡扇发动机的平衡方程为：1) 混合室进口的两股流体的静压平衡；2) 尾喷管喉道的流量平衡。当方程组迭代计算平衡时，实际上只能够保证发动机部件流量连续，高压涡轮与压气机、低压涡轮与风扇之间的功率平衡将不能够保证，涡轮功率与压气机功率之差，就是功率提取法中的额外功率。这样实现任意给定高压压气机喘振裕度(或增压比)，并方便地获得双轴涡扇发动机加、减速控制规律。

4 舰载机/涡扇发动机一体化计算算例

结合已知的舰载机数据确定推重比和机翼载荷, 基于上述分析以及给定的约束条件，得到舰载机的翼载/推重比约束关系如图5所示。

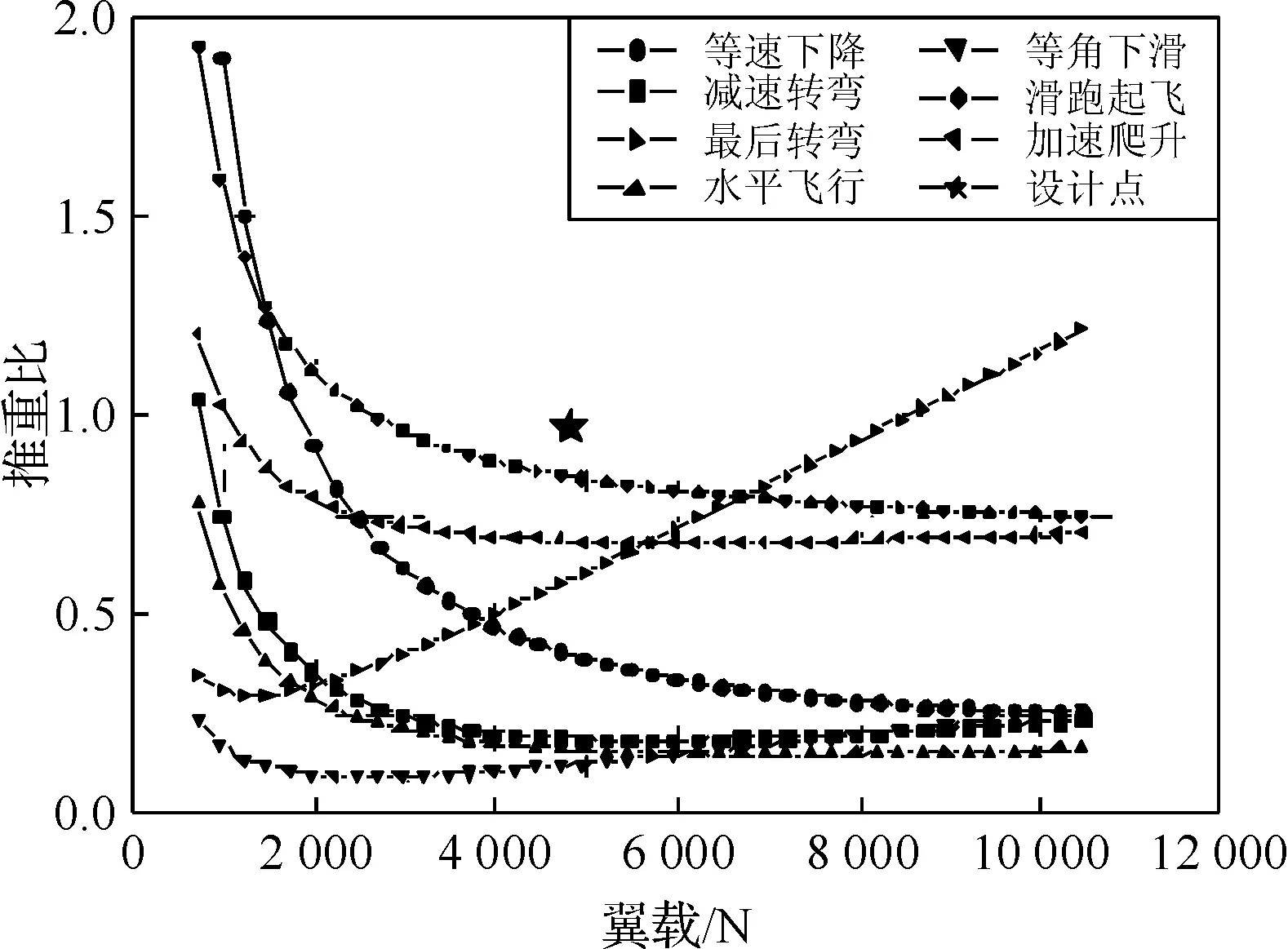
图5 舰载机翼载/推重比约束关系

通过计算可知, 在满足舰载机推重比和机翼载荷的条件下, 各航段均满足逃逸条件。通过约束分析发现, 舰载机在舰上滑跑逃逸时, 滑跑距离对约束分析影响较大。因为舰载机逃逸时, 以一定速度触舰并要在较短的滑跑距离内加速到最小起飞速度, 故滑跑距离变化, 继而约束边界随之变化。

由于研究舰载机复飞, 要求复飞时起飞段的发动机状态为85%高压转速加速至最大状态。按照第3节分析方法，结合发动机控制规律得到新的供油规律为:W=W85%+ 0.942t,W85%为发动机状态为85%的供油量。其中，进口条件为:飞行高度H=0 km, 飞行马赫数Ma=0.147。原加减速控制对应的供油规律为：W=W85%+0.628t。获得的发动机加速性能如图6所示。

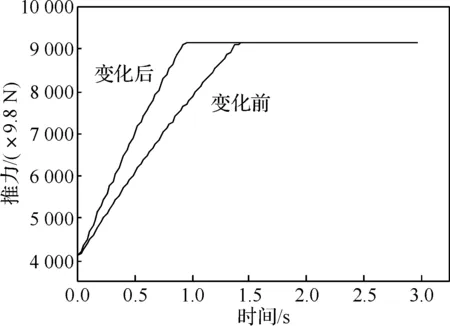
(a) 推力加速特性对比

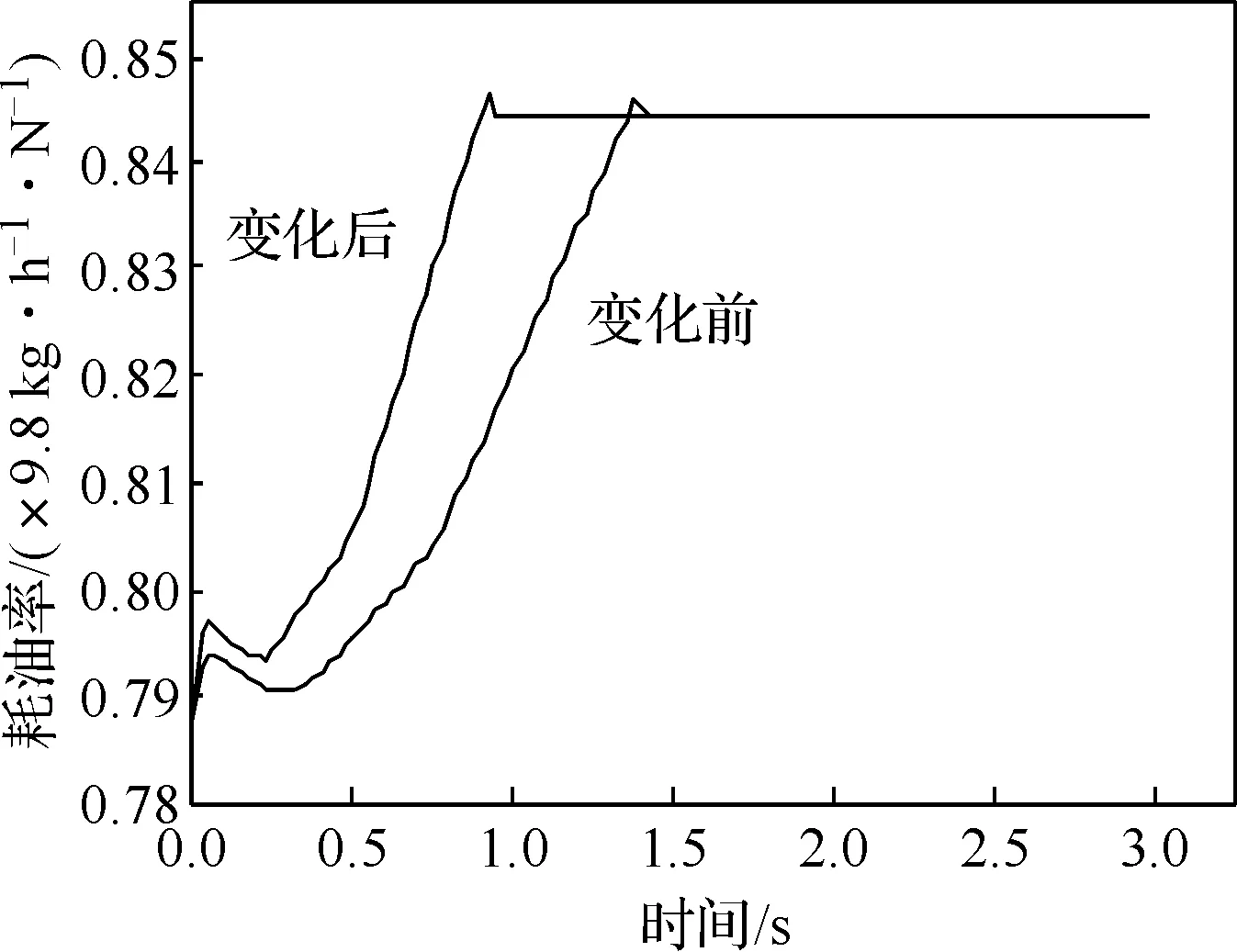
(b) 耗油率加速特性对比图6 发动机加速特性对比

由图6可以看出, 加减速规律改变后, 推力在更短的时间内增加到最大, 相应的耗油率消耗的更快。在新的加速供油规律下, 推力和耗油率能有更快的响应。由前述分析可知, 随着喘振裕度的增加, 稳态工作点(图4的B点)逐渐靠近喘振边界,在满足喘振裕度限制、高压涡轮进口温度限制以及燃烧室余气系数限制的条件下, 尽可能增加喘振裕度，充分挖掘发动机潜力, 直至获得允许的喘振裕度最大值, 由此获得最佳的发动机加速性能。

舰载机着舰时可能面临不同的甲板风，由于不同的甲板风会对逃逸性能有影响，为了在有限的甲板长度上成功逃逸，所以舰载机就要控制相应的着舰重量，经过计算得出不同甲板风对应的最大着舰重量，结果如图7所示。

图7 不同甲板风和最大着舰重量比的关系

由图7可以看出当甲板滑跑长度一定时，最大着舰重量随着甲板风的提高相应提高，此图为舰载机在不同甲板风着舰时的重量控制起参考作用。

根据改进后的加速控制规律对舰载机进行逃逸性能评估, 计算出当甲板风为25 kn时，不同的β值相对应的甲板滑跑长度, 结果如图8所示。

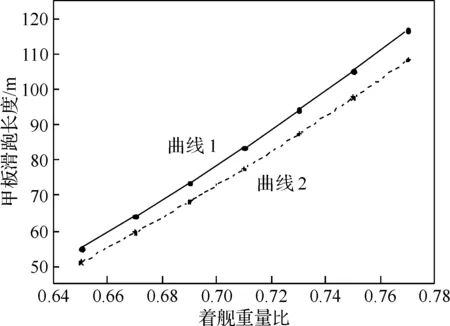
图8 着舰重量比和甲板滑跑长度的关系

图8中曲线1为发动机原加速控制规律计算结果, 曲线2为采用功率提取法得到的发动机加速控制规律计算结果，可以看出发动机加速控制规律经改进后，对于同样的β值，舰载机逃逸所需甲板滑跑距离明显减小。

当β值为0.67时，在两种控制规律下分别计算出不同甲板风所对应的舰载机甲板滑跑距离情况，结果如图9所示。

图9 甲板风和甲板滑跑距离的对应关系

图9中曲线1为发动机原加速控制规律计算结果，曲线2为采用功率提取法得到的发动机加速控制规律计算结果，可以看出发动机加速控制规律经改进后，同样的甲板风，舰载机逃逸所需甲板滑跑距离明显减小。

综合图8和图9分析可得，利用改进后的加速控制规律可以有效地减小舰载机逃逸时所需的甲板滑跑长度, 提高着舰重量从而留给舰载机驾驶员更多的反应时间, 提高舰载机逃逸的成功率。

5 总结

基于涡扇发动机部件模型和飞机气动模型, 以舰载机着舰过程为典型剖面,依据能量法建立飞/发一体化控制模型。以此为基础, 开展对舰载机着舰复飞技术的研究，得到的主要结论如下:

(1) 将舰载机着舰过程划分为7个阶段,各航段均满足逃逸条件。通过约束分析发现, 舰载机在舰上滑跑逃逸时, 滑跑距离对约束分析影响较大。

(2) 基于功率提取法设计的加减速控制规律, 与原控制规律相比, 能最大限度地发掘发动机潜能, 推力在更短的时间内增加到最大。

(3) 根据改进后的加速控制规律对舰载机逃逸性能进行评估, 可以有效地减小舰载机逃逸时所需的甲板滑跑长度、提高着舰重量。当甲板滑跑长度一定时, 最大着舰重量随着甲板风的提高相应提高。