公平关切下零售商主导闭环供应链的定价策略
姚锋敏, 刘 珊, 胡宪武, 滕春贤
(1.哈尔滨理工大学 经济与管理学院,黑龙江 哈尔滨 150080; 2.温州商学院 管理学院,浙江 温州 325035)
0 引言
随着经济全球化的不断推进,产品进行更新的速度也不断变快,由此也产生了越来越多的废旧产品,如何对废旧产品进行有效的回收及再利用引起了社会各界的普遍关注。而利用逆向供应链进行废旧产品回收及再制造是减少废弃产品的有效途径,因此包含逆向供应链的闭环供应链已经引起广泛关注[1,2]。
近年来,国内外学者对渠道权力对闭环供应链定价决策及回收渠道选择的影响进行了不少研究。国外著名学者Savaskan等首先针对闭环供应链的最佳回收渠道设计进行了深入研究,结果表明当原始设备制造商作为渠道领导者时,则由零售商回收最优[3]。Choi等分析了不同主导力量对闭环供应链相关决策的影响,并对比了闭环供应链系统总利润41]。Jena等在闭环供应链内新产品销售及废旧产品回收都存在竞争的前提下,分析了不同合作模式对闭环供应链内价格及回收策略的影响,并表明闭环供应链成员企业全合作时是最优的[5]。Wei等在闭环供应链内综合考虑了信息对称性及渠道权力,研究了不同渠道权力结构下信息是否对称对闭环供应链定价及回收决策的影响[6]。国内不少学者分别基于渠道领导力[7]、价格竞争[8],回收模式[9]等问题做了更深入的研究。上述文献尽管从不同角度探讨了闭环供应链的相关决策问题,但并未考虑企业决策偏好行为对闭环供应链决策的影响。
目前,大多数学者针对供应链进行的研究几乎都基于理性“经济人”假设,而Ho等进行了一系列的实验表明人们在现实中进行决策时总是伴随某种行为偏好,并进一步证实了在供应链中公平关切行为依然存在[10]。因此一些学者开始在供应链的研究中考虑成员企业的公平关切性。如Kumar等研究了公平关切性对销售渠道关系维持的影响[11]。Cui 等针对制造商主导的供应链系统,研究了公平关切对渠道协调的影响[12]。Katok等研究了公平关切行为对于供应链内协调契约达成的影响[13]。Yang等研究表明当零售商公平关切时,在一定条件下合作广告策略可以协调供应链[14]。国内不少学者也对此类问题进行了跟踪研究[15~17]。特别的,不少学者还将公平关切行为引入到服务供应链[18]、农产品供应链[19]等正向供应链优化及运作领域,从不同角度揭示公平关切行为的影响。
近些年也有学者开始考虑公平关切行为对闭环供应链决策的影响。张克勇等在是否考虑零售商公平关切两种情形下构建了决策者的利润模型[20]。丁雪峰等通过设计合理的契约实现了闭环供应链成员企业之间的有效协调[21]。韩小花等运用实验及理论模型研究了决策者的决策偏好对闭环供应链定价策略及成员企业的公平偏好影响[22]。刘志等研究发现,关注再制造商公平关切与不关注相比,新产品与再制造品销量更高;制造商不关注再制造商公平关切时,再制造商利润与公平关切程度负相关,应采用再制造收益共享契约来进行供应链协调[23]。在由单个原始设备制造商、单个再制造商以及两个分销商构成的闭环供应链中,陈章跃等研究指出分销商在市场中的讨价还价能力与制造商的公平关切行为并无明显关联[24]。上述文献少有研究同时考虑制造商与零售商的公平关切行为,分析主导零售商负责回收时对废旧产品回收率产生的影响。
现实中,随着京东、苏宁等零售企业的发展,已在不少行业形成了零售商主导的闭环供应链系统。同时,由于闭环供应链同时涉及正向的销售及逆向的回收,其决策环境相对也更为复杂,渠道利润的分配也更难保证公平合理。此时,闭环供应链成员企业更容易产生对公平行为的关注。
基于此,本文将针对零售商主导同时考虑成员企业产生公平关切时的定价决策问题进行深入的探讨,首先分析了制造商的公平偏好行为对自身利润、经济效用以及对闭环供应链其他成员企业与系统整体绩效产生哪些影响;其次,分别探讨了制造商与零售商的公平偏好程度与产品销售及废旧产品回收之间存在怎样的关系。这些关键性问题将是本文的主要研究内容。
1 问题描述与基本假设
本文考虑一个完全信息对称下单周期的闭环供应链结构,为了将全部精力集中在产品研发及再制造中,制造商将委托负责销售产品的零售商进行废旧品的回收,零售商掌握先行的决策权并与制造商进行Stackelberg博弈。需求函数如下
D(p)=a-βp
(1)
其中a表示新产品市场最大份额,a>0。p表示零售商售卖新产品价格,β为价格敏感系数,β>0。一些相关变量及符号如下:
w为零售商向制造商购买新产品的批发价格;m为零售商通过出售产品赚取的单位利润,m=p-w;cm与cr分别表示制造商的单位生产成本以及对废旧品进行二次加工的单位再制造成本,cf制造商对零售商的单位转移支付,要求cm-cr-cf>0;c(τ)=kτ2表示零售商回收废旧品的总成本,其中τ为零售商的回收废旧品率,0≤τ≤1,k为规模参数,代表零售商回收废旧品的困难程度。
由于回收率具有一定界限性且为了保证文中相关表达式有经济意义。类似文献[3,7]等的假设,我们要求规模参数k应足够大,即满足
2 不考虑公平关切行为时闭环供应链的最优决策
为了便于分析闭环供应链中成员企业的公平关切行为会对产品的定价以及各成员利润的获取产生怎样的影响,本节将首先探讨零售商与制造商均不考虑公平关切行为时的情形,此时企业利润达到最大化将是所有成员企业的最终目标。此时两者的决策顺序为:1)零售商率先宣布零售价p和回收率τ;2)制造商再根据p与τ制定批发价,此时两者的利润函数可以分别表示为
πr(p,τ)=(p-w)D(p)+cfD(p)τ-kτ2
(2)
πm(w)=(w-cm)D(p)+(cm-cr-cf)D(p)τ
(3)
接下来,将采用传统的逆向递推法来解决供应链中常见的博弈问题。
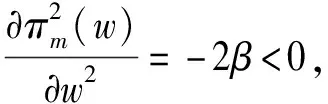
(4)

(5)
(6)
然后,将p*代到公式(1)中,即得到消费者对该产品的最大需求量为
(7)
接着,将p*与τ*代到公式(4)中,求得该产品的最佳批发价为
(8)
其中,令2k-β(cm-cr)(cm-cr-cf)=Δ1,6k-β(cm-cr)2=Δ2,8k-β(cm-cr)2=Δ3。
最后,将上述均衡结果代到公式(2)~(3)中,可求得主导零售商与制造商的最大利润分别为
(9)
(10)

(11)
其中,令12k-β(cm-cr)2=Δ4。在规模参数k的假设条件下,易证Δ1,Δ2,…,Δ4>0。
3 考虑公平关切行为时闭环供应链的最优决策
3.1 制造商考虑公平关切行为时的最优决策
本节之所以探讨制造商具有公平关切行为时的决策问题,原因在于处于领导地位的零售商往往会获得较供应链其他成员企业更多的利润[25],处于供应链上游企业的制造商会因付出与回报不匹配而产生不公平的心理倾向,参照国内该研究领域的权威学者杜少甫[15]以及张克勇[20]等的假设,将制造商具有公平关切倾向时的效用函数表示为
um=πm-λm(πr-πm)
(12)
其中λm由0到1表示制造商的公平关切程度由弱到强,且主导零售商充分掌握制造商公平关切程度λm的大小。
与第2小节的决策过程相似,依然采用逆向递推法对该问题进行求解,不同之处在于,此时的制造商会因自身的公平关切倾向追求自身经济效用最大化而不是企业利润最大化。限于篇幅原因,具体求解过程将不做赘述。
当制造商考虑公平关切行为时的均衡结果如下所示。(将用加下角标“λm”的形式来表示制造商具有公平关切倾向时的均衡结果)
(13)
(14)
(15)
(16)
其中,令6k(2λm+1)-β(λm+1)(cm-cr)2=Δs,2k(4λm+1)-β(λm+1)(cm-cr)2=Δ6,8k(2λm+1)-β(λm+1)(cm-cr)2=Δ7。
将公式(13)~(16)代到零售商与制造商的利润函数中,求得二者的最大利润分别为
(17)
(18)

(19)
(20)
其中,令12k(2λm+1)2-β(λm+1)2(cm-cr)2=Δs,4k(2λm+1)2-βλm(λm+1)(cm-cr)2=Δ9。在规模参数k及制造商公平关切程度λm的假设条件下,易证Δ5,Δ6,…,Δ9>0。
3.2 制造商与零售商同时考虑公平关切行为时的最优决策
在3.1小节研究的基础上,本节将进一步探讨当供应链成员均具有公平偏好时的最优决策问题,此时零售商的效用函数可以表示为
ur=πr-λr(πm-πr)
(21)
其中λr由0到1表示零售商的公平关切程度由弱到强,同时制造商也充分掌握着零售商公平关切程度λm的大小。当制造商与主导零售商均会产生公平关切倾向时的求解过程同第2小节相似,此处不做赘述,具体表达如下(将用加下角标“λ”的形式来表示制造商与零售商同时具有公平关切倾向时的均衡结果)

(22)
(23)
(24)
(25)

3.3 均衡结果分析


通过对性质1的分析结果表明,λm的增大有利于制造商自身效用的增加。这是因为,在具有主从博弈关系的供应链研究中,大多数学者的研究结果均表明,相比于供应链中的其他成员企业,处于核心地位的主导企业总是会获得更多的利润。此时,上游企业制造商可能会因为自身的收入与付出不匹配而产生公平关切倾向,进而以追求自身经济效用最大化为最终的决策目标。
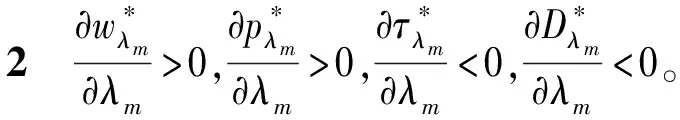
证明根据公式(13)~(16),易证
其中,令4k-β(cm-cr)cf=Δ14。在规模参数k的假设条件下,Δ14>0,证毕。
通过对性质2的分析结果表明,λm的增大使得新产品的批发价格与零售价格均有所上涨,同时降低了消费者对新产品的市场需求及废旧产品的最佳回收率。


证明根据公式(17)~(19),易证
其中,令8k(2λm+1)-β(5λm+2)(cm-cr)2=Δ15。在规模参数k及制造商公平关切程度λm的假设条件下,易证Δ15>0,证毕。
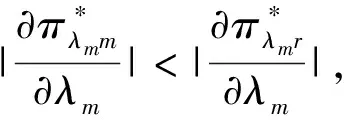
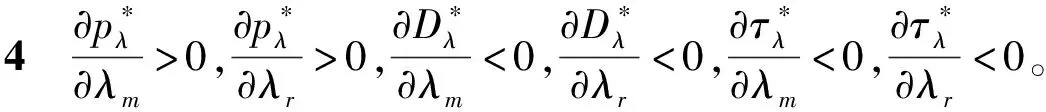
证明根据公式(23)~(25),不难验证
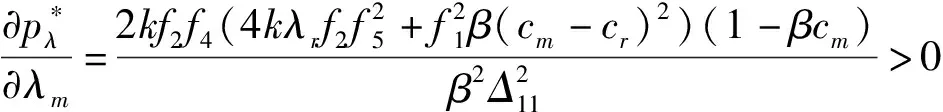
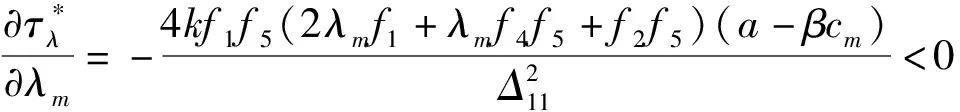
对性质4的分析表明,供应链成员企业的公平关切行为均会导致新产品零售价格的增涨,同时造成新产品市场需求及废旧产品最佳回收率的降低。同性质2的原理是相似的,同时具有公平关切倾向的制造商与主导零售商,均会追求各自的效用最大化。因此,他们将通过提高批发价格与零售价的营销手段来提高自身效用,但这一措施必然会对产品的市场需求造成严重的影响,从而导致正向供应链中的经济下滑。与此同时,在逆向回收中,主导零售商也会通过降低回收成本的方式来减少自身利润的损失。
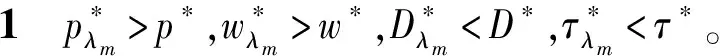
证明根据公式(5)~(8)以及公式(13)~(16),易证
其中,令16k-β(cm-cr)(cm-cr-4cf)=Δ16,在规模参数k的假设条件下,易证Δ16>0,证毕。
由定理1的研究结果可知,同不考虑公平关切时的情形相比较,当闭环供应链中的成员企业具有公平关切倾向时,该种行为会导致产品的价格上涨,进而造成消费者对该产品市场需求的减少,降低了产品在市场中的竞争力及占有率。毫无疑问直接影响到废旧品的回收效果,不利于环境的保护及经济的可持续发展。

证明根据公式(9)~(11)以及公式(17)~(19),易证

其中,令8k-3β(cm-cr)2=Δ17,16(3λm+1)k-β(5λm+2)(cm-cr)2=Δ18。在规模参数k及制造商公平关切程度λm的假设条件下,Δ17>0,Δ18>0,证毕。
由定理2的研究结果可知,首先从经济效益角度而言,同不考虑公平关切时的情形相比较,具有公平关切倾向的制造商会获取更大的经济效益,但制造商的该种行为会造成零售商以及供应链系统整体的利益受损。其次,从环保角度而言,因制造商一味追求效用的提高而影响了零售商在供应链中的正常运营,不仅经济上惨遭损失,也严重影响了废旧产品的回收效果,从而使闭环供应链管理得不到稳定有效运行。

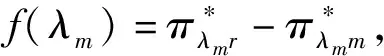
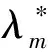
现有公平关切下闭环供应链的运作研究表明,各企业获取的渠道利润会因成员的公平关切行为而进行重新分配(例如,张克勇[20],丁雪峰[21]等)。而本文的研究进一步表明,闭环供应链成员的公平关切行为虽然对自身总是有利的,但不一定对闭环供应链系统整体有利。
4 数值仿真分析
本节通过数值算例对本文研究的主要结论进行验证。假设本文出现的相关参数分别为α=260,β=1,cm=9,cr=6,cf=0.9,k=115。
在制造商以及零售商的不同公平关切程度(系数)下,相关仿真结果如图1~图5所示。

图1 零售价格与回收率随着制造商公平关切系数的变化趋势

图2 供应链中各成员企业及系统利润随着制造商公平关切系数的变化趋势
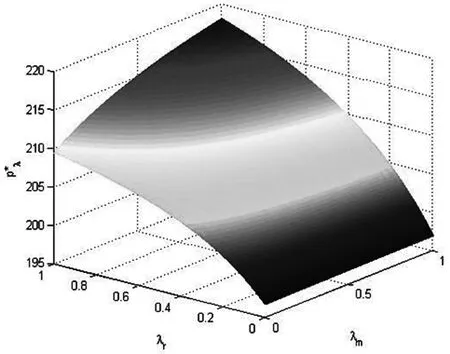
图3 新产品零售价格随着参数λm与λr的变化趋势

图4 废旧产品回收率随着参数λm与λr的变化趋势

图5 产品需求量随着参数λm与λr的变化趋势
通过对图1的观察可以看出,制造商公平关切程度的增大不仅导致产品价格的上涨,也同时影响了市场中废旧产品的回收效果,因此无论是从加强市场竞争力还是从实施可持续发展角度,供应链中的核心企业不仅注重自身效益的增加更应关注其他成员企业的心理状态,这样才能实现整个供应链系统协调有序的运行。这进一步验证了本文性质2的相关研究结果。
由图2可以看出,制造商公平关切程度的增大对自身企业利润的增加起到一定的促进作用,但抑制了零售商企业利润的增长,同时系统整体的总利润也呈现出下滑的趋势。由此可以看出,制造商公平关切程度的增大对零售商的影响更加显著。通过对图2的进一步观察发现,随着公平偏好程度的增加,会导致主导零售商的企业利润低于制造商,因此为了维持闭环供应链系统协调有序的运作,零售商应该采取有效措施积极应对制造商的公平关切倾向,避免对闭环供应链系统及其他成员造成更大损失。这进一步验证了本文性质3及定理3的相关研究结果。
通过图3~图5可以看出,供应链成员企业的公平关切行为均会导致新产品零售价格的增涨,同时造成新产品市场需求及废旧产品最佳回收率的降低。由此可知,当闭环供应链中的成员企业产生公平关切倾向时,对新产品在市场的竞争力以及提高废旧品的回收效果均会产生不利的影响。
5 结论
本文所研究的闭环供应链成员企业包含单个主导零售商和单个制造商,并分别基于成员公平中性、制造商公平关切以及两者同时公平关切三种情况,构建了相应的利润决策模型,通过对不同决策模型下均衡结果的分析比较,得出如下结论:1)随着制造商公平关切程度的增大,新产品的批发价及零售价会随之增加,但新产品销量及废旧产品回收率却随之减少;2)制造商公平关切程度的增大会促进制造商企业利润及经济效用的增加,但抑制了零售商利润的增长;3)与成员公平中性或考虑公平关切时的情形相比较,在成员公平中性时新产品零售价格更低,新产品市场需求及废旧产品回收率均更高;4)同不考虑成员公平关切时的情况比较,当制造商具有公平关切倾向时,该行为始终有利于自身利润及经济效用的增加,但不利于主导零售商及闭环供应链整体总利润的增加;5)与不考虑成员公平关切时的情况比较,成员企业的公平关切行为均会抑制产品的销量及废旧品的回收。本文研究的闭环供应链系统中的成员企业均是信息对称的,且假定产品的需求函数为线性的,接下来可以进一步考虑供应链成员竞争以及市场需求不确定时闭环供应链的最优决策问题。

