城市突发事件中基于事故演变的救援需求决策模型及其优化求解
杨 枫, 叶春明, 种大双
(1.河南中医药大学 管理学院,河南 郑州 450046; 2.上海理工大学 管理学院,上海 200093)
0 引言
随着社会经济的快速发展,城市的规模变得越来越大,建筑物越来越密集,人口越来越多,道路也越来越拥堵。城市发生突发事件的几率在增大,上海外滩的踩踏事件、天津港特大爆炸事件等城市突发事件给城市管理者敲响了警钟。突发事件发生后,快速的应急响应和救援措施能有效的防止事态蔓延,减少次生灾害。
应急资源的分配要结合事故点的救援需求来确定,它的特点是需求数量远远大于供应数量,而且带有突发性和紧急性特点。应急资源的分配必须满足应急反应时间更短,资源利用率更高的要求,比一般资源的分配更严格。对于突发事件的应急资源分配的研究,国内外学者已经做了大量的工作,取得了不少成果。Bozorgi-Amiri等人考虑救灾物流背景下的不确定问题,以最小化受灾区的最大资源短缺和最大化灾区满意度水平为目标,构建一种多目标随机规划模型[1]。王旭坪等人针对大规模突发事件发生后的初级阶段应急资源的分配问题,提出了一个多目标非线性整数规划模型,并将时间满意度、需求满意度和效用满意度看作目标函数,进行求解[2]。Sheu在基于一个三层的应急物流混合分配框架提出了混合模糊聚类方法进行灾区划分与应急物资分配[3]。王苏生等人建立一种以双层决策方法为基础的多受灾点应急资源配置模型,提出一种多受灾点-多出救点应急资源配置动态优选策略[4]。Arora H等建立了以最大化救助率为目标的应急资源分配模型[5]。Wex F等构建了以总运输时间最小为目标的应急物资分配模型[6]。于辉等研究了应急物资分配的两阶段嵌套策略[7]。葛洪磊等人考虑应急物资分配中灾害严重程度、物资属性和受灾点属性等因素,提出了一种受灾人员损失函数,并以受灾人员损失最小为目标进行求解[8]。Liu C等提出基于Petri网构建多种应急资源在不同应急周期内的分配模型[9]。Wang J等考虑应急资源配置的及时性与公平性, 建立基于双层决策方法的应急资源配置模型[10]。庞海云等基于公平原则建立以系统损失最小为目标的应急物资分配和运输优化模型[11]。薛坤等建立了公平关切下以负效用加权的到达时间最小为目标的应急物资配送优化模型[12]。Sherali H D等基于公平原则构建了以最小化灾害风险为目标的应急物资分配模型[13]。詹沙磊等设计一种通过已知需求灾区对未知需求灾区的救灾品需求进行贝叶斯更新的需求更新方式, 由此建立救灾品公平配送模型[14]。张怡等研究了应急物资公平分配的塔木德分配模型、比例分配模型与Shapley值分配模型[15]。上述研究的主要立足点都是将目标函数归结为损失最小化和分配效用最大化,虽然模型的目标形式都不一样,没有考虑到救援需求随着事故演变发生动态随机改变的现实情况。
城市突发事件具备较强的不确定性和随机性特征,事故状态的演变是无序的,导致救援过程中资源需求数量、交通损坏程度等因素具备随机性;事故状态的演变也是实时的,导致各种次生灾害的变化具备动态性,同时,对突发事件进行决策的有效信息之间存在较强的非关联性和模糊性特征,因此只能通过事故状态的转移特征,实时进行决策,这种状态符合马尔科夫决策过程的前提条件。马尔可夫决策过程(MDP)是一种描述随机过程的数学方法,它描述的是在已知事故的现在状态和所有过去状态的情况下,其未来状态的条件概率分布仅仅与当前状态有关。已经有许多学者将马尔可夫决策过程方法用来研究各种不确定问题和突发事件问题。学者刘学洪分析了突发事件中所获取的信息存在偶然性,很难行程结构化序列,提出一种马尔科夫挖掘算法的突发事件科学决策方法,对突发事件进行重构初始化处理[16]。该方法的目的是处理突发事件的初始化参数,并没有跟踪突发事件完整的状态变化。张艺凡等人研究了地铁运营突发事件中的风险传导规律和耦合关系,并分析了突发事件中不同地铁线路间的影响和系统的稳态特征,构建了基于随机Petri网的同构马尔科夫链模型,旨在找到提高应急响应效率的关键因素[17]。该研究的对象为地铁突发事件中的不同线路,构建了Petri网,考虑的是线路间和站点间的状态影响,与本文的研究对象有很大不同。张仕学等人研究了公共区域的人群异常聚集问题,通过分析移动基站手机接入量,并利用马尔科夫链构建人群密度预测模型,预测人群异常聚集区域发生突发事件的概率[18]。该研究借助了网络图模型,给出了人群密度定义,利用人群转移网络建立人群聚集的转态转移模型,其前提条件是人群的聚集存在较强的关联关系,但是通常情况下的突发事件并非具备强关联关系。董秀成等人对突发事件的不同发展阶段利用马尔科夫预测方法进行动态预测,首先引入模糊理论,做定量分析,然后利用灰色理论处理评价体系中的不确定和不完备信息,最后给出最优决策方案[19]。该研究主要是在决策方法层面进行了分析,并没有考虑突发事件下应急物资分配的随机性和动态性,没有研究物资调配策略。Ning Zd等人考虑到不同移动终端之间的服务质量参数不同,将垂直切换决策问题作为一个马尔可夫决策过程,以最大化期望总回报和最小化平均切换次数为目标,建立奖励函数,对各环节的服务质量进行评估,得到一个平稳的确定性切换决策策略[20]。黄飞腾等人为了分析水位调节系统,提出了基于系统的马尔可夫性假设,并离散化了系统状态,然后描述了系统的动态随机过程,求得系统故障概率[21]。尚永爽等人采用隐马尔可夫模型对系统进行状态评估,以系统长期运行的最小平均费用率为目标,解决系统视情维修问题[22]。Talluri等人以客户选择行为为研究背景,构建了马尔可夫决策过程模型,以嵌套分配策略为最优策略,并证明了模型和估计过程是有效的[23]。李金林等应用马尔可夫决策过程理论和稳健最优化方法建立存量控制的稳健模型,构建了一种稳健竞标价格策略[24]。Sean K等建立了一个马尔可夫决策过程模型来研究在战斗环境中的空中医疗转移的调度策略[25]。Yu A等研究了马尔可夫决策过程在定价策略管理中的应用[26]。
城市突发事件中应急救援的核心是高效率的调度方案,在事故不断演变的情况下,当前的应急调度计划将影响未来的调度计划,当前的调度决策方案对下一个阶段的决策造成影响,并会改变下一阶段的状态,而与过去的状态无关。很显然,这是一个动态决策问题。城市突发事件中待救点的物资需求会随着事故的演变发生变化,这与马尔可夫决策过程的系统的演变取决于状态之间的随机转变非常相似,因此本文在城市突发事件发生后待救点事故动态演变的具体情境下,考虑当前状态对未来状态的影响,针对城市突发事件下应急救援的的特点,将事故演变设计成马尔可夫决策过程,并构建救援需求优化模型,利用智能算法进行求解。
1 基本概念
在城市突发事件发生后,应急救援的首要目标就是确定救援需求,然后制定合理的救援方案,确定供给的救援物资,但是由于突发事件现场的伤亡信息并不能一次性完整获取,事故信息随着时间的推移和事件的演变逐步获得,因此救援需求也随事故的演变而不断发生变化,这是一个动态变化的过程。

根据以上描述,给出事故演变的救援需求问题描述为:
(1)城市突发事件中待救点与救援点地理位置是确定的,救援点与待救点之间道路是连通的。
(2)如果把整个救援时间T分为n个时间段,那么在任一时间段Δti(1≤i≤n),由于存在需求和供给不平衡的情况,所以给出的应急救援方案不一定能满足救援的需求。

由于待救点与施救点之间存在多对多的救援物资分配问题,而且不同施救点之间可以进行物资转运,再加上待救点之间的救援需求随着事故演变和时间推移不断发生变化,这使得解决此类问题变得异常复杂。
马尔可夫决策过程是不确定性系统动态控制的主要方法,广泛应用于随机优化控制、智能决策等领域[27],可以为城市突发事件的救援需求动态决策提供量化模型。马尔可夫决策过程的基本原理是未来状态的分布依据当前状态的概率分布,在此基础上做出判断和决策[28]。马尔可夫决策过程分析方法在城市突发事件中基于事故演变的应急资源优化调度过程中的应用如图1所示。整个决策过程是如何选取方案应对突发事件的事故演变不确定发展的状态,直至突发事件完全被控制为止。

图1 城市突发事件中基于事故演变的应急资源调度过程的马尔可夫决策过程
2 模型描述
2.1 需求状态演变的马尔可夫过程

(1)

(2)
其中,πt表示从阶段t到过程终结的决策规则δ的序列{δt,δt+1,…},πt=(δt,πt+1),其中δt是阶段t的决策规则。有如下性质:
性质1如果在阶段t决策者做出不满足待救点需求的决策,那么随着事故演变该待救点的需求状态一定是阶段t的非递减函数。
很显然,假设待救点在阶段t未能得到救援物资,那么随着事故的演变,该待救点对救援物资的需求量只能是保持或者是增加。有:
(3)
性质2待救点受到各种不确定因素的影响,它在每个阶段的需求状态呈现随机性。
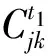
(4)
由性质1可得Pjk是一个上三角矩阵。

(5)
定理1假设G是阶段t+1和阶段t之间的时间间隔,那么有:
(6)
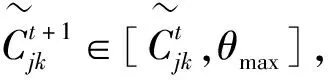
(7)
其中,round()表示对括号内内容按照随机的方法取整,而且取得的整数与自身数值最接近。另外,还需规定一个初始值:
(8)

性质3如果在某个阶段物资调配策略满足该待救点的需求,那么待救点的需求状态将回归到初始状态,但随着时间推移,需求的变化将会遵循由“产生”到“剧烈”的过程。为了区分自然变化状态,做出如下定义:
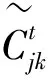
依据性质3,如果在式(7)、(8)中添加影响因子,用以表达待救点的需求满足对需求状态转移概率的影响,那么可以得到阶段t与阶段t-1之间干预状态的转移方程为:
(9)
在求得需求的干预状态后,进一步求出需求表达式,需求表达式的定义如下:

(10)
2.2 基于马尔可夫决策过程的救援需求决策模型
目标函数为:
(11)
(12)

根据物资调配实际情况,还必须增加式(13)的约束:
(13)

3 模型优化求解
3.1 花朵授粉算法
城市突发事件发生后,应急救援要求必须用最短的时间做出物资调度的决策,因此决策模型的求解对算法的收敛速度要求比较高,如果模型的决策变量涉及的维度较多,而且各维度集合规模较大时,求解会比较困难,对算法的要求也高。花朵授粉算法(Flower Pollination Algorithm, FPA)是一种基于群体智能的随机寻优算法,它源于对大自然中花朵授粉行为的模拟[29]。花的授粉方式按照花朵距离的不同,可以分为自花授粉和借助昆虫的异花授粉两种。算法的全局搜索类似于花朵的异花授粉过程,局部搜索类似于花朵的自花授粉过程,全局搜索和局部搜索的比重通过切换概率来权衡,这种方式使算法具有良好的寻优效率,能够求解各种优化问题。
FPA假定每棵植物只开一朵花,每朵花只产生一个花粉配子,且每朵花为求解优化问题的一个解,通过切换概率控制异花授粉和自花授粉之间的转换[30]。它的主要思想是:首先初始化种群,然后对种群个体进行适应值评价,找出适应值最优的个体作为当前全局最优解,最后不断迭代执行异花授粉和自花授粉两个操作过程,直到满足收敛条件为止。
对于花朵授粉算法的形式化描述,建立如下数学模型:
定义4在全局授粉中,传粉载体携带花粉粒进行大范围、长距离搜索,从而保证最优个体的授粉和繁殖。在全局传粉过程中,花粉的位置更新公式为:
(14)
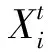
(15)
其中:Γ(λ)是标准伽马函数,参数1<λ≤3,文献[29]指出λ=1.5时算法获得最好的性能,因此本文取λ=1.5。
定义5相邻花朵局部授粉的花粉粒位置更新公式为
(16)

定义6转移概率p是决定花粉粒进行全局授粉还是局部授粉的概率,p为常数,且p∈[0,1]。p值越大则进行局部授粉活动的概率更大,同时进行全局授粉的机会将减少。
由于实际情形中相邻的花朵更容易授粉,因此局部授粉活动发生概率将大于全局授粉。通过参数研究发现,对于优化问题p=0.8是效果最好的参数选择。

3.2 二进制编码下的花粉位置更新

(17)
然后,设计花粉粒子位置更新公式如下:
(1)异花授粉时,
(18)
(2)自花授粉时,
(19)
采用sigmoid函数将花粉位置映射到[0,1]区间,并将更新后的位置转换为取1的概率,即
(20)
设计花粉粒子位置的更新公式为:
(21)
其中ρ~U(0,1)。
3.3 适应度函数设计
为了获得一个独立的适应度函数,将式(13)转换成惩罚函数,合并到式(11)中,得到:

(22)


(23)
求解干预状态等价于对元胞数组的元素进行选择。即
(24)
3.4 算法步骤
用花朵授粉算法求解基于事故演变的救援需求调配问题的步骤如下:
步骤1对算法的控制参数进行初始化,其中花粉粒子规模为M=jmax×tmax,切换概率为p,算法最大迭代次数为nmax。

步骤3进入主循环,如果rand>p,按照式(18)和式(20)、(21)进行异花授粉,否则按照式(19)和式(20)、(21)进行自花授粉。其中rand是[0,1]上服从均匀分布的随机数。


步骤6比较n与nmax,若n≠nmax,则令n=n+1,算法跳转到步骤3,继续花朵授粉算法核心操作,如果n=nmax,算法转到步骤7判断算法终止条件。
步骤7当满足迭代条件时,算法停止,获得最优的调度方案Xg*jt和最优的物资调配量Fitg*。
4 实证
4.1 实例描述
由于突发地震,某市部分地区房屋倒塌,造成人员伤亡,急需药品和食品。假设该市有5个区域需要救援,分别为A、B、C、D和E,如图2所示。随着灾情的发展,待救点对药品和食品的需求不断发生动态演变。假设地震发生后,可能导致4种次生灾害,其对救援资源的需求状态空间为N={N1,N2,N3,N4},需求状态转移概率(P={P1,P2,P3,P4})和救援阶段(S={S1,S2,S3,S4})矩阵和物资需求最低满足量分别为表1和表2所示,假设每个阶段仓库能提供药品50千克,食品600千克。

图2 待救点分布图
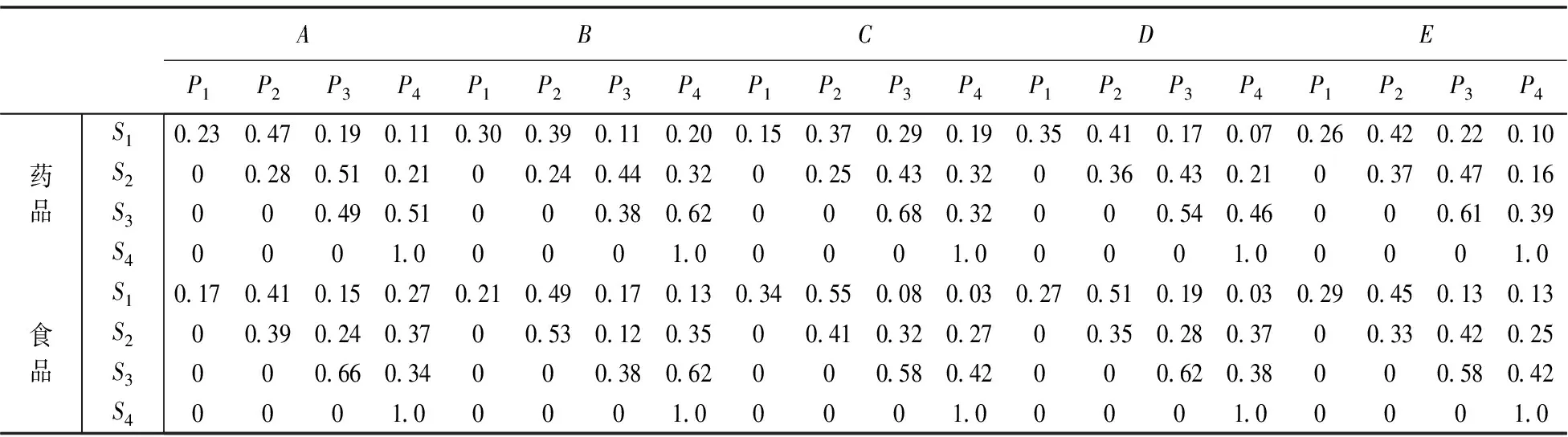
表1 待救点对药品和食品的需求状态转移概率矩阵

表2 待救点对物资的初始需求和已有物资量(单位:吨)
由于突发事故,救援资源准备不足,不可能同时满足所有地区的救援物资的需求,只能分阶段逐步的满足。如何选择先满足哪些地区后满足哪些地区,每个阶段提供多少物资,是解决问题的关键。很显然,随着事故演变,救援需求也在动态变化,其状态转移概率具有马尔可夫性。基于马尔可夫决策过程的应急物资调度决策方案针对待救点实时需求状态的演化特征,做出合适的需求满足决策,其目的是保证事故整体的需求状态平稳,合理配置资源,实现救援需求的优化,更好的实现救助任务。因此,考虑事故演变的不确定性,必须动态的给出合理的物资调配策略,对每个待救点采取逐步满足的方式,使得整体的物资需求呈缓慢变化趋势,并降低物资的整体需求量,避免过度调配。物资调配策略的思想是对伤员多,物资需求增长较快的待救点优先进行物资调配,并加大调配量,然后随着系统状态的演化逐步调整调配方案,确保整个应急物资的调配过程保持平衡,并尽可能的保证公平性和效率性。
4.2 求解过程
为了验证本文所提出的花朵授粉算法解决4.1实例中基于事故演变的需求物资调配问题的有效性,在CPU为Intel Core i7 2.5GHZ,内存为4GB的计算机上编程求解,使用的操作系统为64位Windows 7,编程工具为Matlab R2015b。为了更好的说明算法的运行结果,对同一问题,分别采用花朵授粉算法、粒子群算法和萤火虫算法进行编程求解,并做出对比。3种算法的初始参数如表3所示,针对每种算法程序均独立运行10次,对食品和药品调配策略分别求解,结果如表4所示。

表3 FPA、FA和PSO算法参数设置

表4 FPA、FA和PSO算法对药品和食品物资需求优化方案10次运行结果
从表4中可以看出,3种算法都能获得最优物资调配结果,10次运行的结果可以看出花朵授粉算法求解的目标函数最优值相比粒子群算法和和萤火虫算法都小,说明为了达到待救点物资需求的平稳增长,花朵授粉算法得到的物资调配策略使得在整个救援过程中待救点物资调配量最小,更加合理的利用了救援物资。
取第6次运行结果绘制最优目标求解收敛曲线,如图3所示。

图3 FPA、FA和PSO算法对食品和药品物资最优调配策略迭代曲线
从图3可以看出,花朵授粉算法求解该类问题的收敛速度比粒子群算法和萤火虫算法都快,说明了花朵授粉算法有更快的寻优能力,符合应急物资调配的时间要求。由第6次运行结果,由式(1)、(11)、(17)、(21)、(22)、(23)、(24)将花朵授粉算法的最优粒子位置反向取值获取最优物资调配策略为如下图4矩阵:
图4说明,对于待救点区域A、B、C、D和E,在4个阶段的药品物资调配中,1011表示对区域A的物资调配中第1阶段满足待救点的需求,第2阶段不满足,第3、4阶段满足其需求,同理对于区域B、C、D、E分别对应矩阵的2、3、4、5行的策略,策略选择的依据是该待救区域事故演变的程度和需求量的大小。
5 结论
城市突发事件中待救点的救援物资需求会随着事故的演变发生变化,这种演变是不确定的,而且明显具有马尔可夫性。在救援物资不能满足所有待救点的需求情况下,必须采取合理的物资调配策略才能保证各个待救点的救援需求平稳变化,不至于出现物资严重不足导致受灾人群的恐慌,造成更严重的后果,也不至于出现物资过度调配,造成物资的浪费和调配的不均衡。本文在城市突发事件发生后待救点事故动态演变的背景下,将应急救援需求的演变设计成一个马尔可夫决策过程,并构建优化模型,然后利用花朵授粉算法对模型进行求解。最后,以某市突发地震灾害,造成药品和食品短缺为例进行实证研究。结果表明,本文提出的救援物资需求决策模型使用马尔可夫决策过程方法,模拟事故演变中待救点物资需求动态变化过程,并做出合理的需求满足决策,可以合理的配置资源,使整体救援需求保持平稳的状态,实现了救援需求的优化,更好的完成救助任务。因此,突发事件情境下事故演变存在随机性和动态性,这种不确定演变符合马尔可夫性特征,对此类问题的决策可以采用马尔科夫决策过程方法进行处理;应急救援背景下,物资需求的产生与演化与物资调配策略有直接关系,对多种需求的满足属于多目标优化问题,必须平衡多个目标的需求关系才能尽可能延缓需求的产生和演变,所以以整个救援阶段物资需求的总和最小为优化目标更能贴切说明这个问题,这也是突发事件中应急救援的特征:平稳演变,大局为重。

