金属中溶质相互作用的机器学习研究
何康尼, 孔祥山, 刘长松
(1.中国科学院 固体物理研究所 材料物理重点实验室,安徽 合肥 230031;2.中国科学技术大学,安徽 合肥 230026;3.山东大学 材料科学与工程学院,山东 济南 250061)
引 言
点缺陷是金属晶体中的主要缺陷之一,广泛存在于金属晶体中。外来的替代和间隙溶质原子是常见的点缺陷,它们的存在和相互作用对金属材料的微观结构以及演变有重要影响,进而影响或支配材料的诸多性质,如强度、硬度、延展性、导电和导热性等等。替代和间隙溶质原子之间的相互作用可以由它们分离足够远的体系总能量和在一起时的体系总能量之差来表征,这种能量差被称为结合能或相互作用能,本文称其为结合能。表征溶质相互作用的结合能既具有重要的基础研究价值,也具有实际的工程意义。由于实验上的一些限制,对金属中溶质结合能的研究主要来自于理论计算。近年来,基于密度泛函理论的第一性原理计算成为研究溶质结合能的主要工具。Kong等[1]运用第一性原理计算系统研究了W中过渡金属(transition metal,TM)溶质与H之间的结合能,评估了金属溶质对H溶解和扩散的影响,为有关的H滞留实验结果提供了合理的解释。除此之外,包含不同溶质的多种合金体系也已得到研究[2-23]。虽然第一性原理计算能给出精度很高的数据,但也存在计算量大、耗时长的不足,需要很高的计算成本。不同金属基体、不同替代溶质和不同间隙溶质的组合数目巨大,其中还有大量组合体系没有被计算和研究,通过第一性原理计算的方法穷尽这些组合体系来得到所需数据是难以实现的。
机器学习(machine learning,ML)是一种强大的方法,有可能从根本上改善和提高材料科学领域的计算效率[24]。这种方法从已有的数据中学习规律、建立模型,进而对新数据进行预测。只需要极小的计算成本,ML就可以预测出海量的未知数据,同时可以对数据进行多维分析。ML方法有多种类型,常见的有支持向量机(support vector machine,SVM)[25]、人工神经网络(artificial neural network,ANN)[26]和决策树(decision tree,DT)[27]等。随着ML的发展和进步,其已被成功应用于多个领域[24]。近期,Ubaru等人[28]使用SVM分析和预测了二元TM合金的生成焓。Wu等人[29]使用四种不同的ML方法,研究了面心立方(face-centered cubic,fcc)金属基体中替代溶质的扩散能垒。Zeng等人[30]使用梯度增强的DT方法研究了fcc、体心立方(body-centered cubic,bcc)和密排六方(hexagonal close-packed,hcp)金属基体中间隙轻溶质的扩散活化能。这些研究证明了ML对于提高计算效率、加速新材料发现的有效和成功。然而,很少有研究运用ML研究金属基体中溶质之间的结合能,这阻碍了人们对这一物理内容的理解和相关研究的进展。
本文使用SVM方法研究了金属中替代金属溶质与间隙轻溶质之间的结合能。以物理或化学属性构建基本特征集,并通过对特征进行优化,得到一组最优的特征组合。进而对数据进行拟合、交叉验证和外推测试,并以极小的计算成本预测出大量新合金体系的结合能数据,这些数据可供有关的理论和实验研究参考。
1 研究方法
1.1 数据集
数据集来源于课题组前期计算数据和从已发表文献中收集的计算数据[1-23],一共包含310个替代金属溶质和间隙轻溶质的结合能。涉及8种金属基体,包括bcc金属V、Fe、Nb、Mo和W,fcc金属Ni、Pd,以及hcp金属Ti;涉及的替代金属溶质以TM为主,也包括碱金属、碱土金属和其他金属等;涉及的间隙轻溶质为H、He、C、N和O,它们是常见的间隙元素。两溶质原子之间的结合能可以由下式计算[10]:
(1)

进行成功预测的一个关键步骤是使用一组重要特征,这些特征应支配或影响目标值。根据先前的研究[1,3,5-6,10,14-18],选择以下17个特征作为基本特征集:金属基体的原子半径Rh、体积模量Bh、熔点Th、未成对的d电子Zh、鲍林电负性Eh和原子序数Nh,替代金属溶质的原子半径Rs、体积模量Bs、熔点Ts、未成对的d电子Zs、鲍林电负性Es和原子序数Ns,以及间隙溶质的原子半径Ri、熔点Ti、未成对的电子Zi、原子序数Ni和溶质浓度Ci。这些特征被总结在表1中。在进行训练和测试之前,把所有特征的数值缩放至0到1之间,每种特征的最小值对应为0、最大值对应为1。
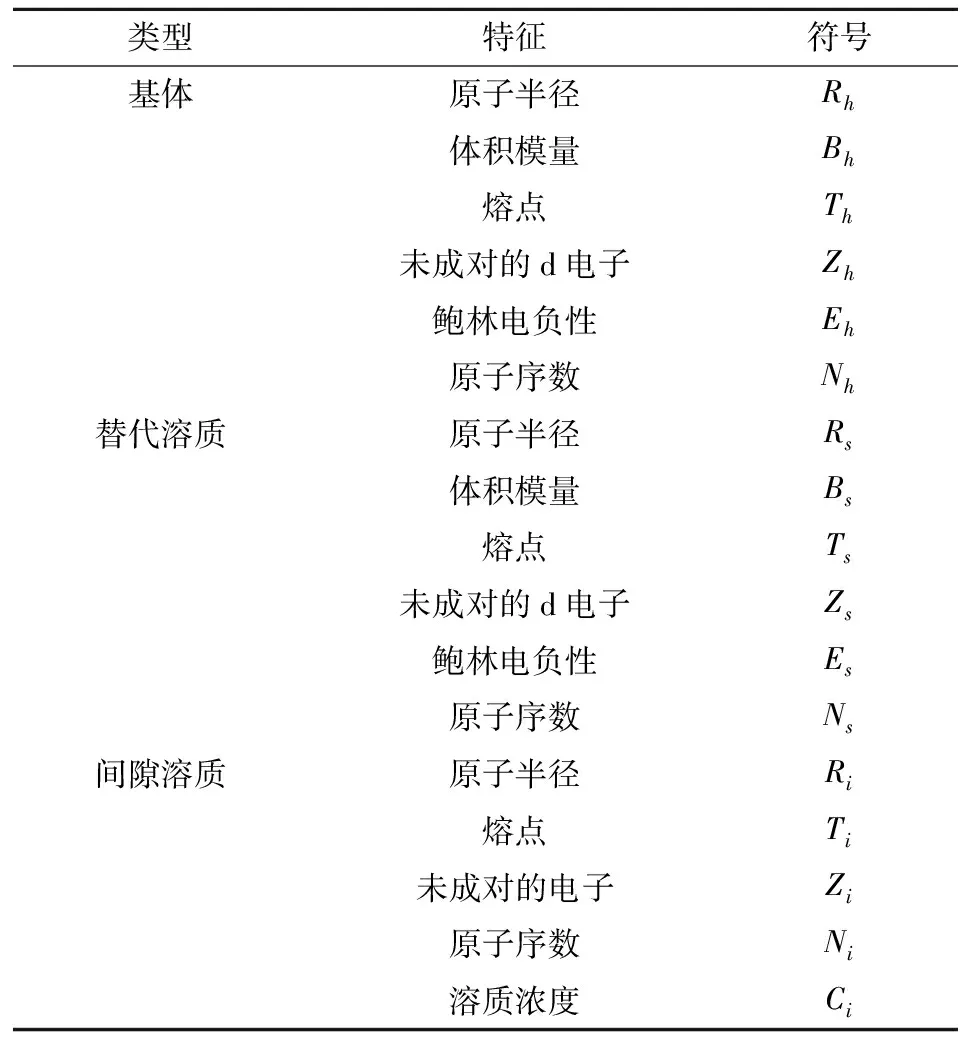
表1 基本特征集
1.2 支持向量机方法
本文采用的方法是SVM回归算法[25],使用的核函数为径向基函数。SVM是一种流行的ML方法,建立在统计学习理论的基础上,适合处理小样本、多维和非线性问题。在SVM建模过程中,不敏感误差、惩罚参数C和核参数γ能被调整以建立不同的模型。经过测试,发现模型的预测效果对较小的不敏感,因此在后文的计算中被设置为0.01。使用10折交叉验证和网格搜索法[31]对C和γ的值进行优化,图1显示了使用网格搜索法进行参数优化的流程图。为了衡量预测结果的优劣,使用均方根误差(root mean square error,RMSE)和平方相关系数(squared correlation coefficient,γ2)作为度量标准,它们由下列公式定义:
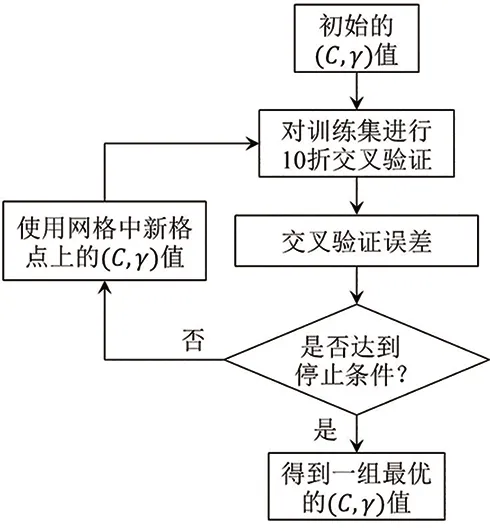
图1 网格搜索法的流程图
(2)
其中,f(xi)是预测值,yi是训练值。对于RMSE,其值越小代表预测效果越好,理想值是0。对于r2,其值在0到1之间,越接近1表明相关性越强,1代表理想情况。本文的所有计算均使用LIBSVM MATLAB软件包[31]完成。
2 结果与讨论
2.1 特征和参数优化
当进行网格搜索时,C和γ值的变化范围被设置为2-10至210,变化步长(即网格大小)都为20.5。因此,共有41×41=1681对(C,γ)值被计算。当把所有的(C,γ)计算完,可以得到一组最优的(C,γ)值,利用此(C,γ)值建立的模型即为最优模型,具有最好的推广性能。图2显示了运用网格搜索法计算得到的交叉验证RMSE,使用的特征集为表1列出的所有特征。当C=28、γ=2-2.5时,RMSE达到最小值0.109 eV。遵循和上面类似的过程,使用不同的特征组合建立不同的模型。表2列出了多种不同特征组合的计算结果。

表2 不同特征组合的详细信息

图2 运用网格搜索法计算得到的交叉验证RMSE,使用的特征集为表1中列出的所有特征
如表2所示,与熔点和原子序数相比,当从所有特征中去掉未成对的d电子或原子半径时(对应的特征组合为“All-Zh,Zs,Zi”和“All-Rh,Rs,Ri”),预测效果显著下降。当从所有特征中去掉体积模量、鲍林电负性和原子序数中的一种或几种时,预测效果变化很小或反而变好。对于组合“All-Bh,Bs,Nh,Ns,Ni”,预测效果达到最优,其RMSE为0.103eV。当仅用一种特征(Zh,Zs,Zi,Th,Ts,Ti,Rh,Rs,Ri,或Nh,Ns,Ni),或仅用基体、替代溶质或间隙溶质的特征(Rs,Bs,Ts,Zs,Es,Ns,Rh,Bh,Th,Zh,Eh,Nh,或Ri,Ti,Zi,Ni,Ci),预测效果都较差,特别是仅用基体或替代溶质的特征时,对应的RMSE超过0.3 eV。这些结果与人们对溶质之间相互作用的理解是一致的,溶质之间的相互作用是一个复杂的过程,涉及多种物理因素的综合影响、难以用单一物理量描述。同时,相互作用的过程涉及基体原子、替代溶质原子和间隙溶质原子之间的协同效应,而不单单由某一种原子决定。由于组合“All-Bh,Bs,Nh,Ns,Ni”具有最好的预测效果以及较少的特征数量,因此被选择作为最优特征组合,本文使用这一组合和其对应的最优(C,γ)值进行后续的计算。
2.2 拟合和预测
使用最优的特征组合和(C,γ)值对整个数据集进行训练,可以得到预测模型。图3(a)显示了拟合预测值和训练值的比较,这些拟合预测值由模型对已知训练值的预测得到,其中不同的橙色点对应不同的合金体系,黑色实线y=x代表预测值和训练值相等的理想情况。从图中可以看到,除了少量数据外,预测的结合能和训练数据没有明显的偏差。通过计算,可得RMSE=0.049eV,r2=0.982,表明拟合效果良好。为了进一步验证模型的预测效果,使用留一交叉验证(leave-one-out cross-validation,LOO CV)进行训练和预测。具体来说,每次使用309个数据进行训练建模,对剩余的1个数据进行预测。把这一过程重复进行310次,就可以预测出所有310个数据。图3(b)显示了由LOO CV预测的数据与训练数据的比较,对应的RMSE=0.102eV,r2=0.923。RMSE达到一个较低的水平,r2超过0.9,表明预测值与训练值之间具有高度相关性,这表明所选特征能很好地反映目标值结合能。

图3 (a)拟合预测值和训练值的比较;(b)LOO CV的预测值和训练值的比较
基于由已知数据集得到的模型,进而对新的、未知的数据进行了预测。具体而言,对8种金属基体(Ti、V、Fe、Ni、Nb、Mo、Pd、W)、24种替代TM溶质(3d系列Ti、V、Cr、Mn、Fe、Co、Ni、Cu,4d系列Zr、Nb、Mo、Tc、Ru、Rh、Pd、Ag和5d系列Hf、Ta、W、Re、Os、Ir、Pt、Au)和5种间隙轻溶质(H、He、C、N、O,其浓度被设置为1/128)的8×24×5的960个合金体系的结合能数据进行了预测(具体数据可向作者索取),包含对部分已有数据的预测。需要指出的是某些合金体系可能并不存在,为了数据完整性也对它们的数据进行了预测。本文以极小的计算成本得到了一个全面的结合能数据库,这些数据可以为后续有关的理论和实验研究提供很有价值的参考,如可以为相关的多尺度模拟计算提供必要的输入参数、以研究更大体系中溶质的行为。
2.3 对新体系的预测效果
虽然交叉验证过程能对模型的预测效果提供有效的整体评估,但当预测全新的基体和间隙溶质体系时,模型的预测能力依旧未知,并且,这种预测具有较强的挑战性。因此,接下来进一步测试了SVM模型对新基体-间隙溶质体系的预测/外推效果。具体而言,把某一种基体-间隙溶质数据选出作为测试集,而把剩余的所有数据作为训练集;对于挑选出的测试集,基体和间隙溶质分别为一种固定的元素,仅替代金属溶质不同。此外,把测试集中的数据逐渐取出加入到训练集中,以此来观察训练集对测试集的预测效果如何随增加的数据而改变。图4显示了被测试的基体-间隙溶质体系分别为V-C、Fe-C和Ni-C时,预测效果随训练集被加入的测试集数据量的变化情况。图5显示了Ti-O、V-O和W-O的相关结果。图6显示了W-H、W-He的相关结果。图4和图5属于间隙溶质相同而基体不同的情况,而图6结合图5中的W-O则属于基体相同而间隙溶质不同的情况。图4-6中的每个数据点为100次计算结果的平均值,同时,标准差也被绘出以表征数据的波动情况。

图4 对V-C、Fe-C和Ni-C新基体-间隙溶质体系的预测效果随被加进训练集的数据量的变化情况
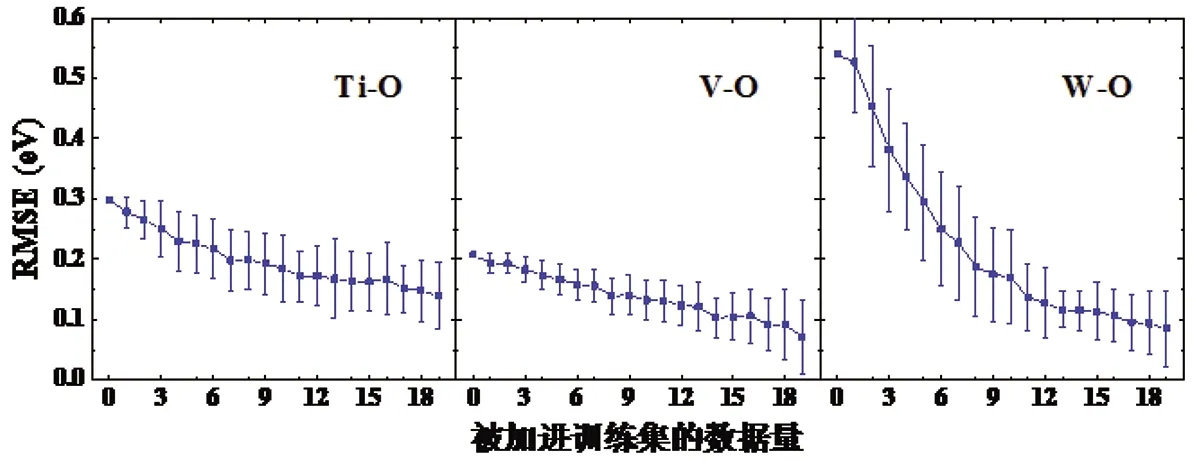
图5 对Ti-O、V-O和W-O新基体-间隙溶质体系的预测效果随被加进训练集的数据量的变化情况
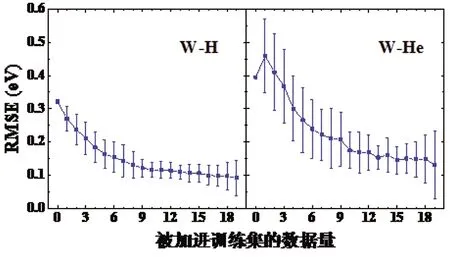
图6 对W-H、W-He新基体-间隙溶质体系的预测效果随被加进训练集的数据量的变化情况
从图4中可以看出,对三种不同基体体系的预测效果差别较小。当训练集完全不包含来自测试集的数据时,对Fe-C的预测误差RMSE为0.106 eV,而对于V-C和Ni-C其RMSE均小于0.1 eV。随着测试集的数据被逐渐加进训练集,RMSE逐渐减小。从图5中可以看出,当训练集完全不包含来自测试集的数据时,对W-O的预测效果明显差于Ti-O和V-O,其RMSE高达0.539 eV。这可能是由于W具有最高的熔点和电负性,以及较大的半径。另外,和训练集里其他金属基体属于3d-和4d-TM不同,W是唯一一种5d-TM。这些因素可能导致对W基体系的整体预测效果较差,这一结论可在图6中W-H和W-He的结果上得到反映。随着测试集的数据被逐渐加进训练集,RMSE同样逐渐减小,对于Ti-O、V-O和W-O当训练集分别包含来自测试集的7个、1个和8个数据时有RMSE<0.2 eV。由图6和图5中的W-O计算结果可知,当训练集完全不包含来自测试集的数据时,对W-He和W-O的预测效果较W-H更差。对于W-H和W-He当训练集分别包含来自测试集的4个和10个数据时有RMSE<0.2 eV。另外,W-He数据的标准差在所有被计算的体系中最大,即预测效果的波动性最大。这可能是由于这里所考虑的4种间隙溶质中He的数据量最少,导致对W-He的预测结果较不稳定。通过对这些新基体-间隙溶质体系的测试,可以了解对没有数据或数据有限的新基体-间隙溶质体系进行预测时的预期误差大小。
3 结论
使用基于SVM的ML方法,本文研究了金属中替代金属溶质与间隙轻溶质之间的结合能。结合课题组前期计算数据和从已发表文献中收集的数据,获得了一个包含310个结合能的数据集。17种物理或化学属性被选择作为基本特征集。通过对特征进行优化,得到一组最优的特征组合。基于最优的特征组合和模型参数,对数据集进行了拟合和LOO CV。拟合得到的RMSE=0.049eV,r2=0.982,表明拟合效果良好。LOO CV得到的RMSE=0.102eV,r2=0.923。RMSE达到了一个较低的水平,r2超过0.9,这验证了所使用的最优特征组合能很好地反映结合能。进而,对960个合金体系的结合能数据进行了预测,这些预测以极小的计算成本获得,可以为后续有关的理论和实验研究提供很有价值的参考。最后,测试了SVM模型对新基体-间隙溶质体系的预测效果,通过这些测试可以了解对没有数据或数据有限的新基体-间隙溶质体系进行预测时的预期误差大小。本文的研究表明ML是提高计算效率、加速材料科学研究的一种很有前景的方法。随着数据量的增加,ML方法能够被更广泛地应用于材料科学领域。

