PLF.sets的实证研究及其高质量仿真应用

刘玉成，王传生，杨露鑫，理查德·丁

(1.南京财经大学 国家重点实验室，江苏 南京 210023; 2.首都经济贸易大学 信息学院,北京 100070; 3.对外经济贸易大学 国际经济研究院,北京 100029; 4.美国波士顿克罗诺斯研究所,波士顿 02101- 02117)

0 引言

受益于计算机逻辑学(Computer logic)、心灵哲学(Philosophy of mind)、玄学(Metaphysics)和语言哲学(Philosophy of language)等学科知识的发展，逻辑否定、反对(contrary)和矛盾(Contradictory)概念的内涵[1～3]得到了进一步的丰富，使得模糊系统运算的复杂性有了少许简化。20世纪末，朱梧槚和肖奚安[4]在计算知识应用系统中提出了Medium Logic(即，M L)，也就是中介逻辑系统的概念。接着，Esteva等人[5～7]将一类新的一元联结词“～”、“┐”和“∃”等，融合到严格基本逻辑(SBL)中，形成带有对合否定的严格基本逻辑(SBLIN)，构建形如:┐x=x→0的逻辑关系等。而文献[2]中研究的广义亚里士多德对立方形图(GASO)的形式化理论是引入了中性量词后，定义了Contradictories, contraries and sub-contraries的概念。当满足：A┐(u)=n(A(u))的条件，称A┐为A的n矛盾否定集；而当满足：A∃=(A+B-U)且A∃(u)+A(u)≤1的条件时，则互为对立否定集。哲学逻辑与模糊集知识的不断更新，为两者高效性的融合应用而夯基垒台。

为了更加高效、稳定且高质量地仿真北京市城市人口迁移与演变趋势的实际情况，基于Zadeh模糊集的关系之上，本研究深度改进了Zadeh的经典定理、逻辑转化、运算规则及特征属性。并结合PLF.sets方法实证和实际应用的具体要求，创新性地提出了泛逻辑性模糊集(Pan logic fuzzy sets, PLF. sets)。PLF.sets模糊集融合逻辑否定和计算机哲学，并根据PLF.sets方法实证和人口迁移与演变趋势仿真需要，选择了符合隶属函数g(x)为非线性要求的PLF.sets系统适用类型(即，g(x)函数表达式局部可建立，但整体未知；在确定的值域U内，任意的可映射于g(x)值)。这也是本研究的一点创新和贡献所在。

在确定适用的系统类型后，本文对PLF.sets方法进行《管理信息系统》教学质量评价的实证研究。研究结果证明，PLF.sets方法可以化繁为简，简化运算方法和步骤；显示出高效性、准确性、普适性和简洁性的特点。最后，将PLF.sets方法应用于北京城市人口迁移与演变趋势的仿真。仿真结果表明，PLF.sets高效地逼近了城市人口流动规律；准确地评估了人口流入城市的人口变化情况。并揭示我国首都与国内其它城市之间人口流动网络的类小世界性和核心城市之间人口整体流动数值幂律分布的规律；高质量地反映了正向迁移城市-北京的城市人口迁移与演变趋势的真实情况。

1 前期知识准备

1.1 逻辑符号

本研究所提PLF. sets方法于实际应用中逻辑符号的定义：A(x)、A～(x)、A┐(x)及A∃(x)。

1.2 评价等级及含义

(1)定义评价因素集：U={u1,u2,…,um}；其中Ui中i的取值：i=1、2、…、m。

(2)评价等级变量通常引用字母V表示，即：V={v1,v2,…,vm}；其中Vi中i的取值：i=1、2、…、m。

若选取“城市人口流动网络及其关联度”指标为研究对象，则可将评价等级定义成：多、较多、中等、较少及少的概念。

1.3 逻辑应用函数

假设“城市人口流动网络及其关联度”特征的评价符号，分别是：A(x)、A～(x)、A┐及A∃(x)；那么，严格对应的逻辑含义，则依序是：多、较多、中等、较少及少。

综上，将上述逻辑符号整合成具体应用函数[16,17]，公式如下:Fn(x)=A(x)+A～(x)+A┐+A∃。

2 PLF.sets的提出

2.1 定义

根据不同逻辑否定的程度和对应值域范围集合的大小，可设定A为原始局部模糊子集。若有A∈F(u)，且所有的U满足：∀∈U，t-模用*来表示，补算子用字母n表示，其中a、b分别表示为U值的两边端点。那么，泛逻辑性模糊集PLF.sets及其若干逻辑否定之间的关系，可表述如下:

2.1.1假设A为局部定义，在值域U[0,1]内，若存在映射A∃，满足:A∃=(A+B-U)且A∃(u)+A(u)≤1的条件，那么称A∃确定的模糊子集为A的对立否定集。

2.1.2假设A为局部定义，在值域U[0,1]内，若存在映射A┐，满足:A┐(u)=n(A┐(u))的条件，那么称A┐确定的模糊子集为A的n矛盾否定集。当n为线性补时，则A┐(u)=n(A(u))=1-A(u)确定的模糊子集为A的矛盾否定集。

2.1.3假设A为局部定义，在值域U[0,1]内，若存在映射A～，满足:A～(u)=A┐(u)*(A∃)┐(u)=n(A(u))*n(A∃(u))=n(A(u))*n(A(a+b-u))的条件，那么称A～确定的模糊子集为A的*-n中介否定集。当t-模用*来取最小值Min，n取线性补时，称A～(u)=min{1-A(u),1-A(a+b-u)}为A的中介否定集。

此外，基于PLF.sets对Zadeh模糊集中基本特征的继承性，同时经过反复论证，得知其模糊子集之间的并、交、分配等逻辑运算规则具有同一性(Zadeh已证)。自然，PLF.sets也蕴含以下定理:

2.1.4假设A，B满足PPN.定义，若有∀u∈U，及A(u)≤B(u)，那么，A⊆B；当∀u∈U且A(u)=B(u) 时，那么A=B。

2.1.5假设A，B满足PPN.定义，若有∀u∈U，那么，有并的隶属度函数:(A∪B)(u)=A(u)∪B(u)=max{A(u),B(u)}。

2.1.6假设A，B满足PPN.定义，若有∀u∈U，那么，有交的隶属度函数:(A∩B)(u)=A(u)∩B(u)=min{A(u),B(u)}。

2.2 性质

本研究综合PLF.sets的定义、定理和公理，严密推导出PLF.sets的模糊集。所得PLF.sets的性质不同于其它LF.sets等一般模糊集。于最根本的逻辑关系层面来理解，PLF.sets应用了中介否定、矛盾否定及对立否定等否定集的概念；集合相与、相或、相异、包含关系、替代关系及排斥关系等各逻辑运算关系。并将计算机逻辑与哲学否定有机融合于其中，产生具备运算严密性、简洁性、准确性及高效性的特有属性。本研究实证与应用所需的运算规则与逻辑转化等相关性质，阐释如下。

2.2.1A⊆B⟺B┐⊆A┐;A⊆B⟺B∃⊆A∃,A⊆B⟺B～⊆A～。

2.2.2 (A∪B)～=(A∪B)┐∩(A∪B)∃┐

=(A┐∩B┐)∩(B∃∪B∃)┐

=(A┐∩B┐)∩(A∃┐∩B∃┐)

=(A┐∩B∃┐)∩(A┐∩B∃┐)

=A～∩B～

2.2.3A～=A┐∩A∃┐;(A∪B)～=A～∩B～;

2.2.4 (A∪B)┐=A┐∩B┐,(A∩B)┐=A┐∪B┐;

2.2.5 (A∪B)∃=A∃∪B∃,(A∩B)∃=A∃∩B∃;

2.2.6 ∀u∈U,A∃∃(u)

=A∃(a+b-u)

=A(a+b-(a+b)-u)

=A(u)

∴A∃∃=A

2.2.7 ∀u∈U,A∃～(u)

=min{1-A∃(u),1-A∃(a+b-u)}

=min{1-A∃(u),1-A(u)}

=min{1-A(u),1-A(a+b-u)}

=A～(u)

∴A～=A∃～

2.3 PLF.sets仿真系统的设计

根据PLF.sets方法实证和人口迁移与演变趋势仿真应用需要，选择符合隶属函数g(x)为非线性要求的PLF.sets系统的适用类型。即：g(x)函数表达式局部可建立，但整体未知；在确定的值域U内，任意的x∈U可映射于g(x)值。

基于模糊系统严谨的结构设计，及其隶属函数的严格性、正规性和完备性的特征，逻辑转化2.2章节中的系列公式和定理；并引用算子、模、计算机逻辑及哲学否定，对模糊系统逻辑性运算转换规则加以充分的证明(篇幅原因，不再赘述)。证明过程中产生PLF.sets方法实证和人口迁移与演变趋势仿真应用所需的重要规则和定理，阐述如下。

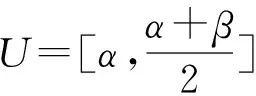
定理2设A是U=[α,β]上PLF.sets的模糊子集，且存在A的对立否定集A∃，那么模糊子集A对应的*-n中介否定集A～和对立否定集A∃，均在U中具备完备性和严格性。式中：t-模用*来表示，n表示补算子。

基于上述PLF.sets系统适用类型中局部特征隶属函数g(x)的可建立性，模糊系统在逼近g(x)的整体函数时，假设有满足任意的输入值X，(x∈U)，其对应于输出数据的值域，可表示为:(x,g(x))的形式。那么，兼顾人口迁移与演变趋势评价的特点，可用以下方法来实现PLF.sets模糊系统函数的整体性。运算步骤如下：

(1)

式中：i1=1,2…N1;…;in=1,2,…Nn。

依据定理1和2的性质，运用公式(1)中模糊中心均值Ci1,Ci2,…,Cin的算法[18～20]，和Mamdani的蕴涵算子：∀a,b∈[0,1],a→b=ab，并取代数积算子的乘积推理法，步骤(1)中的IF-THEN结合规则架构的系统函数f(x)，表示为如下的数学形式:

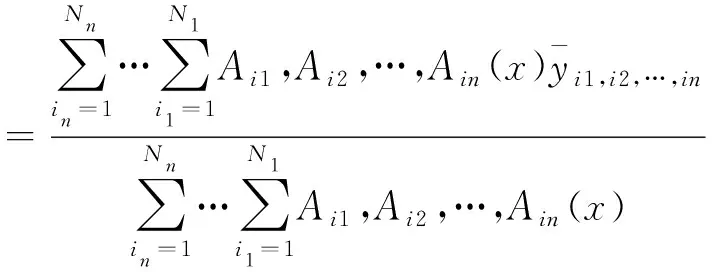
(2)

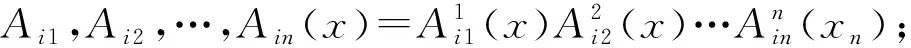
Bi1,Bi2,…,Bin(x)

(3)

本章运用逻辑否定中的替代法则：整体模糊系统中的子集A，相对于对立否定集A∃(x)、*-n中介否定集A～(x)和矛盾否定集A┐(x)等，就是U上严格性、正规性和完备性的其他模糊子集。验证性证明了隶属函数从局部到整体实现的方法与推导过程，最终逼真形成函数F(x)的完整表达式。即，Fn(x)=A(x)+A～(x)+A┐(x)+A∃(x)。

3 PLF.sets的实证研究

为实证PLF.sets评估方法的高效性、准确性、普适性和简洁性等特点，本研究选取普通高校实验教学《管理信息系统》课程的实际教学质量评价进行深入研究。

3.1 教学质量的源数据

首先采集《管理信息系统》课程实际教学的源数据，再由统一化处理后得到各类评价指标数值。部分数值，展示如下。

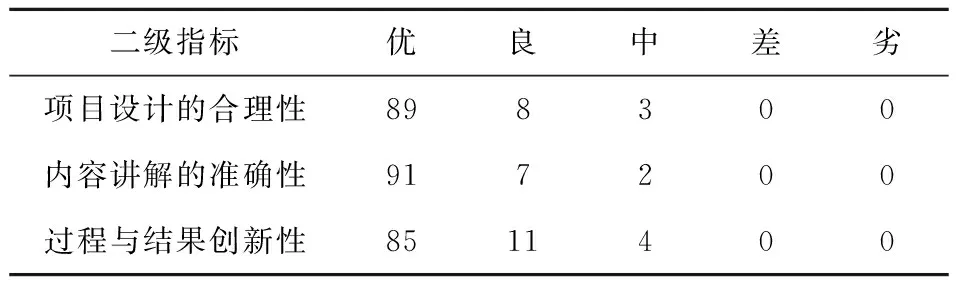
表1 评价标准和等级

3.2 教学质量的评估模糊集

根据PLF.sets定义，可将《管理信息系统》实验课程教学质量的各评价等级采用：A(x)、A～(x)、A┐(x)和A∃(x)等函数式来表达。沿用v来表示模糊子集A(x)，对应定性评判等级即为“优”；并将逻辑关系式严格映射于相应的定性评价集。如此，完成归一化后《管理信息系统》实验课程教学质量之评价因数的整体归集。具体数值(表2)，列举如下。

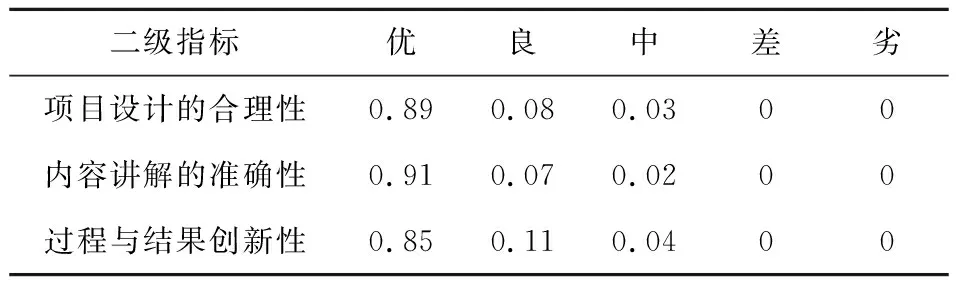
表2 归一化数值表

3.3 评估矩阵的构建

采用g(x)完备且整体性的方法建立《管理信息系统》课程教学质量的评估矩阵，并严格对应地完成对《管理信息系统》课程教学质量的矩阵式评价。以体现对PLF.sets方法的实证效果更具严谨性。

3.3.1 求解隶属函数g(x)

《管理信息系统》课程教学质量对应的模糊局部隶属函数子集为:A1(x)=“优”，A2(x)=“良”等。它相应的局部隶属函数g(x)公式，形式如下。

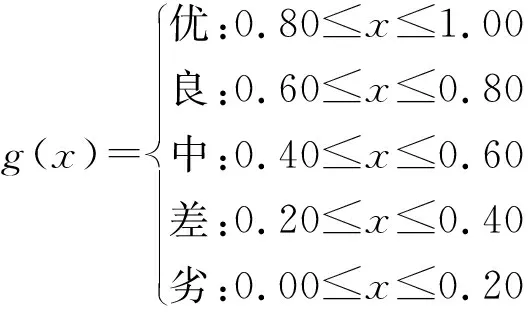
(4)

由本研究第三章所推理形成的哲学否定及逻辑的相关定理，将PLF.sets中教学质量的g(x)转换成f(x)。即:

Fn(x)=A(x)+A～(x)+A┐(x)+A∃(x)

(5)

推进一步，为更好地揭示《管理信息系统》课程教学质量与各级指标参数之间的本质规律和联系，PLF.sets运算中的F(x)建立了严格对应的数学计算表达式。a,b,c及d是F(x)中对应不同否定集的常系数。

Fn(x)=a*A(x)+b*A～(x)+c*A┐(x)+d*A∃(x)

(6)

3.3.2 求解逻辑式

首先，确定《管理信息系统》课程教学质量之隶属函数g(x)；然后，DS融合[21,22]整体函数f(x)；最后，进行教学质量参数指标的逻辑运算[23～25]。结合PLF.sets的定义和性质，《管理信息系统》教学质量指标中项目设计的合理性(即x1)的评价“劣”可视为“优”的对立否定。那么，基于评估模糊集等各环节的依次运算和逻辑，可转变成《管理信息系统》教学质量指标参数“劣”等级的逻辑数组。

根据已知条件U域的两个端点数值分别是:故得:

a=1；b=5

A(a+b)=A(1+5)=A

(6)

∵F2(x1)=A∃(x1)

=A(a+b-x1)

=A(6-x1)

(7)

(8)

由式(10)可知，项目设计的合理性x1的评估数组值为：A(x1)=(0.835、0.071、0.094、0、0)。对标最大隶属度原则的判断标准，可得《管理信息系统》教学质量之“项目设计的合理性”的定性等级是“优”。对表加权平均原则的判断标准数值，该项目设计的合理性的定位同样是“优”等级。

类似的方法，若“内容讲解的准确性”指标(即x2)的评价“中等”，使用中介否定集A～(x)表示；即介于《管理信息系统》教学质量判断等级的“优”与“劣”之间，则可定义成“不优”或“不劣”的概念。那么，根据PLF.sets模糊集相关定理，分别运算“不优”和“不劣”的局部隶属函数，依次得出A┐(x)和A∃┐(x)隶属函数的逻辑形式结果。形式如下:

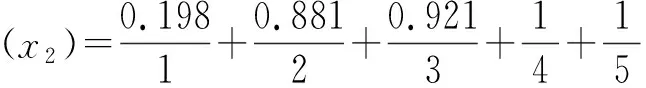
(11)

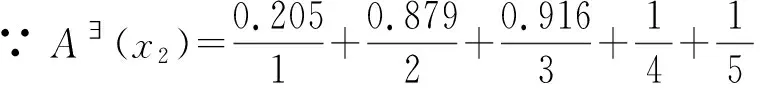
(12)

(13)

至此，本研究代A┐与A∃┐(x)的逻辑结果数值入PLF.sets，进行不同逻辑否定集之间的关系运算，或按照PLF.sets定义3的公式，即:A～(u)=min{1-A(u),1-A(a+b-u)};(u=x2)；得到A～(x)的数组结果。

(14)

然后，联立公式(12)～(14)，得:

(15)

据公式(15)得，内容讲解的准确性x2的评价数组值为：A(x2)=(0.802、0.119、0.079、0、0)。据此，分别对标最大隶属度原则的判断标准和加权平均原则的判断标准，可查内容讲解的准确性的定位均是“优”的等级。

3.4 教学质量的评价矩阵

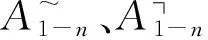
(16)

4 教学质量的综合模糊评价

为高水准地证明PLF.sets方法对《管理信息系统》实验教学的质量评价，符合高效性、准确性、普适性和简洁性等特征；本研究运用模糊综合法对《管理信息系统》教学质量的评价结果进行验证。

4.1 模糊综合法及运行

本研究所运用的模糊综合法对《管理信息系统》实验教学质量的综合模糊评价过程，以及整体的运行步骤如下：

(1)首先，采集同一的《管理信息系统》课程实际教学源数据；

(2)其次，标准化处理后代入AHP[26,27]法则，赋值并运算；

(3)再次，根据各级指标数值与对应权重的M(·,+)合成运算(式17)，得出《管理信息系统》教学质量的评价数组值。M(·,+)算子的具体运算式，即:

(17)

(4)然后，分别单极化和多级化模糊运算，得到各级教学质量相关评价矩阵；

(5)最后，将单因素模糊综合评价矩阵综合，得到最终的综合评价结果。

本研究采用的多级模糊综合法之运行模型的内部结构(图1)，具体如下。

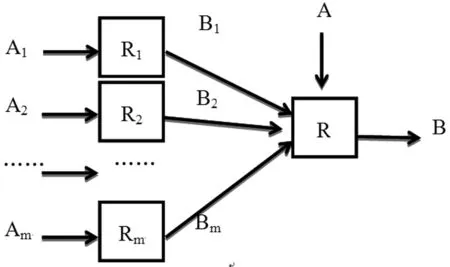
图1 多级模糊综合模型

4.2 综合模糊评价结果

本研究应用AHP[28～30]层级运算，得到A1、A2、…、An等权重(A1[0.2852、0.3347、0.3801]；A2[0.3726、0.3982、0.2292]…)；并采用兼顾性较强的算子对教学质量评价因子进行模糊合成运算,得到如下R1、R2、…、Rn等矩阵(式18)；最终归集得出综合模糊评价数值结果。因篇幅限制，本节所涉及的教学质量评价相关过程数据和矩阵，这里只作简要列举。归纳如下:

(18)

B1=A1·R1=[0.2852、0.3347、0.3801]·R1

=[0.882、0.087、0.031、0.000、0.000]

(19)

B2=A2·R2=[0.3726、0.3982、0.2292]·R2

=[0.911、0.053、0.036、0.000、0.000]

(20)

通过多次循环运算，依次得到B3、B4及B5的单行矩阵式数组。数据如下:

B3=[0.891、0.074、0.035、0.000、0.000]

(21)

B4=[0.806、0.104、0.090、0.000、0.000]

(22)

B5=[0.865、0.083、0.052、0.000、0.000]

(23)

查对上述综合模糊法评估结果数据，易得《管理信息系统》实验教学质量之二级指标(LEVEL2)的评估定性均是“优”等级。自然，项目设计的合理性、内容讲解的准确性及过程与结果创新性的评估定性均“优”。

且对其做进一步验证，可证明《管理信息系统》实验教学质量的整体评估也是“优”等级(篇幅所限，不再详细阐释)。相关结论对应的支撑数据和数值结果，具体如下。

(24)

A=[0.2104、0.2011、0.2007、0.2021、0.1857]

(25)

B=A·R=[0.8711、0.0803、0.0486、0.0000、0.0000]

(26)

注：这里的A代表LEVEL2总权重值，区别于其它。

5 评价结果与分析

本研究运用PLF.sets方法和模糊综合法，分别对具体实验课程《管理信息系统》的教学质量进行了评价验证。通过对照教学质量的最终评价结果，较好地得出了PLF.sets方法具备高效性、准确性、普适性和简洁性的客观结论。

进一步对比《管理信息系统》教学质量评估矩阵中对应指标的评价结果数值，形成了更清晰且更具说服力的细化结论：

(1)两种不同的评估方法对同一《管理信息系统》教学质量的实际评估，互证了各自方法的客观性；并显示了评估结果的一致性；

(2)PLF.sets方法对教学质量的评估过程能够化繁为简，充分体现了高效性和简洁性的优点。

6 人口迁移与演变趋势的高质量仿真

城市人口流动网络及其关联度特征是区域人口迁徙于与演变趋势[31,32]的主要参数指标之一。其具体特征涉及：关联城市个数、关联强度以及城市中心度等典型二级指标。同等体现人口迁徙与演变趋势内质性的主要参数指标，还包括“城市人口流动变化净增加值”这一重要指标。它的主要二级特征指标有：户籍增加量、学籍转入量、医保增加量、疫苗接种增量和居住证保有量等。

本章的仿真应用以我国首都地区为客体对象；采用高效率的PLF.sets方法来准确评估人口流入城市的人口变化情况，并深析人口流入城市的人口流动规律；以期高质量仿真北京城市人口迁移与演变趋势。特别指出，一般情况下，人口迁徙的概念涵盖了通常意义上人口迁移与人口流动的内容范畴；而本研究只是针对人口迁徙中人口流动[33]的内容范畴进行研究。

6.1 人口流动的源数据

随机采集相关指标的数据样本，随后任意选取8000组有效样本数据。经过统一量纲的结构化运算[34]，得到满足PLF.sets方法对城市人口流动变化与趋势计算的过程性数据。部分城市人口流动变化净增加值(一级指标)参数之二级指标数据(表3)的隶属分配情况，展示如下。

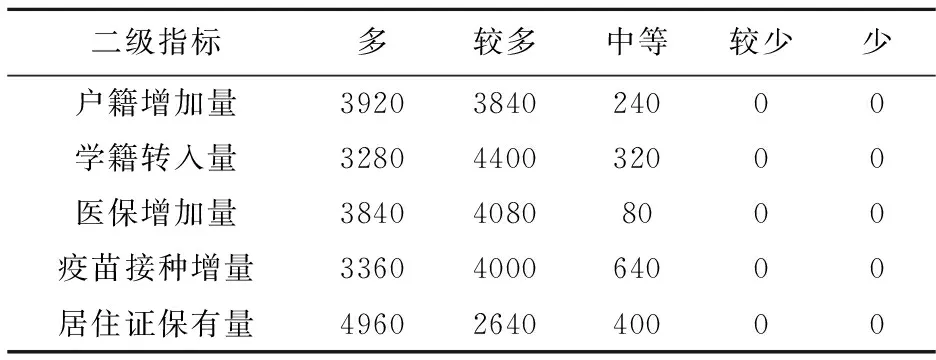
表3 评价标准和等级

同样，随机采集并选取城市人口流动变化与趋势之城市人口流动网络及其关联度特征(一级指标)的相关二级指标数据(表4)1000组。其隶属情况，如下所示。

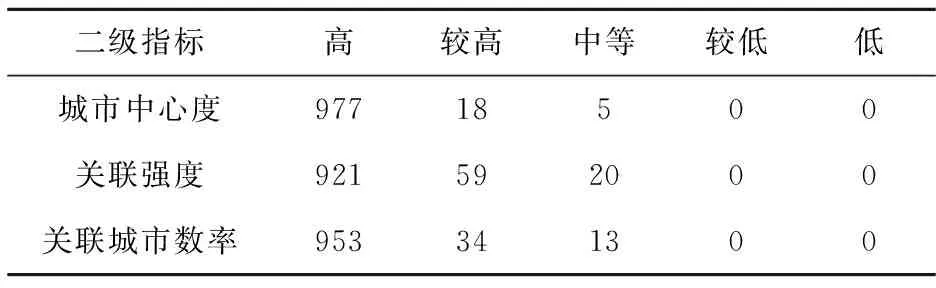
表4 评价标准和等级

6.2 人口流动的评估模糊集

按照PLF.sets的定义，将城市人口流动变化与演变趋势的各个评价等级构建成逻辑式。(如：A(x)、A～(x)、A┐(x)和与A∃(x))。沿用v来表示模糊子集A(x)，定性评判等级为“多/高”等；并将逻辑关系式严格映射于定性评价集。如此，完成归一化后的城市人口流动变化净增加值与城市人口流动网络及其关联度等评价因数的整体归集。具体数值(表5，6)，分别展示如下。

表5 归一化数值表

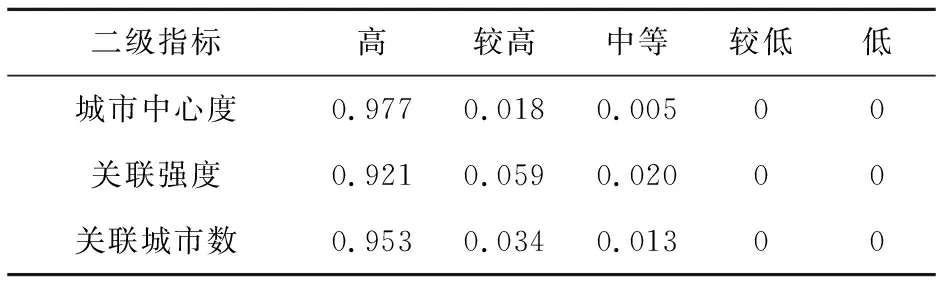
表6 归一化数值表

6.3 评估矩阵一

矩阵一的构建是采用隶属函数g(x)完备性和整体性确定方法，实现对城市人口流动变化净增加值的矩阵评价。有局部隶属函数g(x)向完整隶属函数f(x)转化；再依据函数f(x)构建城市人口流动变化净增加值的评价矩阵。

6.3.1 求解隶属函数g(x)

城市人口流动变化净增加值的判断系统对应的模糊局部隶属函数子集为:A1(x)=“多”，A2(x)=“较多”等。它相应的局部隶属函数g(x)公式，表示如下:

(27)

根据本研究所提哲学否定与逻辑的适用定理，将城市人口流动变化净增加值PLF.sets中g(x)演变为完整函数f(x)。即:

Fn(x)=A(x)+A～(x)+A┐(x)+A∃(x)

(28)

通常情况下，在各LF.sets中运算的A(x)、A～(x)、A┐(x)和A∃(x)存在着对应的f(x)。为了更好地揭示城市人口流动变化净增加值与城市人口迁移与演变趋势之间的本质规律和联系，PLF.sets运算中的F(x)同样须建立以下严格的数学计算表达式(系数a,b,c及d对应F(x)中不同否定集)。

Fn(x)=a*A(x)+b*A～(x)+c*A┐(x)+d*A∃(x)

(29)

6.3.2 求解逻辑式

在城市人口流动变化净增加值隶属函数g(x)的确定后，再经过整体函数的DS融合，进行参数指标的逻辑运算。根据PLF.sets的定义和性质，城市人口流动变化指标中“户籍增加量”指标(即x1)的评价“少”可视为“多”的对立否定。由评估模糊集等各环节的依次运算和逻辑，转换为“城市人口流动变化净增加值”指标参数“少”等级的逻辑数组形式。

由已知条件U域的两个端点数值分别是：a=1；b=5。

可得:A(a+b)=A(1+5)=A(6)

∵F2(x1)=A∃(x1)

=A(a+b-x1)

=A(6-x1)

(30)

(31)

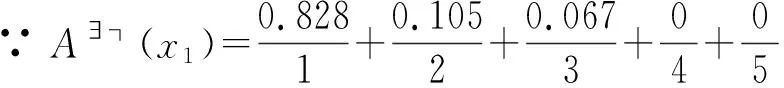
(32)

(33)

因而，得到户籍增加量x1的评价数组值为：A(x1)=(0.817、0.103、0.080、0、0)。此时，参照最大隶属度原则的判断标准，可得城市人口流动变化净增加值之户籍增加量的定性等级是“多”。对表加权平均原则的判断标准数值，该人口流动变化净增加值之户籍增加量同样定位是“多”的等级。

类似的方法，如城市人口流动变化指标之学籍转入量(即x2)的评价“中等”，使用中介否定集A～(x)表示；即介于城市人口流动变化判断等级的“多”与“少”之间，则可定义成“不多”或“不少”的概念。那么，根据PLF.sets模糊集相关定理，分别运算“不多”和“不少”的局部隶属函数，依序得出A┐(x)和A∃┐(x)隶属函数的逻辑形式结果。形式如下:

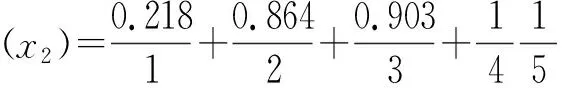
(34)

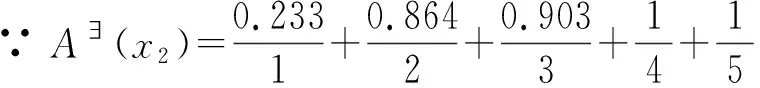
(35)

(36)

于是，将A┐(x)与A∃┐(x)的逻辑结果直接代入以下否定集，进行PLF.sets逻辑运算，或者按照PLF.sets定义3的公式计算(即：A～(u)=min{1-A(u),1-A(a+b-u)}；(u=x2))。具体如下:

(37)

联立公式(35)～(37)可得:

(38)

因此，学籍转入量x2的评价数组值为A(x2)=(0.782、0.134、0.084、0、0)。此时，分别对标最大隶属度原则的判断标准和加权平均原则的判断标准，可知学籍转入量的定位都是“多”的等级。

6.3.3 归集评价矩阵

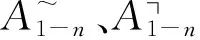
(39)

6.4 评估矩阵二

参照以上相同的方法，首先确定城市人口流动网络及其关联度特征的隶属函数g(x)；其次对整体函数DS融合；再次逻辑计算二级指标；最后将关联城市数、关联强度以及城市中心度等二级指标的参数数值代入PLF.sets逻辑公式，并引用A～(x)、A┐(x)与A∃┐(x)等不同否定集之间的逻辑关系进行运算。最终得到城市人口流动网络及其关联度特征的评价矩阵结果，形如A(x6)=(0.927、0.060、0.013、0、0)等。另外，标题表述的“矩阵二”即指“城市人口流动网络及其关联度特征”矩阵。简要计算过程如下:

(40)

此时，综合A┐(x)、A∃┐(x)与A～(x)等否定集之间的逻辑关系，进行PLF.sets逻辑运算。得到模糊集A～的数组结果，形式如下。

(43)

联立公式(41)-(43)，可以得出A(x)的数组结果为:

(44)

显而易见，本研究城市中心度x6的评价数组值为A(x6)=(0.927、0.060、0.013、0、0)。将x6的数组值分别对标最大隶属度原则的评判标准与加权平均原则的评判标准，可得城市人口流动网络及其关联度特征之城市中心度的定性等级都是“高”级别。

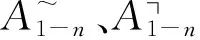
(45)

7 分析与结论

本研究运用准确高效的PLF.sets方法进行逻辑运算，高质量仿真了北京城市人口迁移与演变趋势状况。在分别对学籍转入量等(x1,x2,…,x5)与城市中心度等(x6,x7,x8)二级指标进行逻辑运算后，得到：(1)北京城市人口流动变化净增加值的定位均是“多”的等级(即，表示该城市为人流高输入城市)；(2)北京城市人口流动网络及其关联度特征的定性等级均是“高”级别(即，该城市人流关联核心程度强)的结论。

与此同时，基于北京城市人口流动变化净增加值和人口流动网络及其关联度的各评价矩阵数值，归集得出北京城市人口迁移与演变趋势之PLF.sets法的具体量化评估结果。依据PLF.sets方法所得数值结果，并将其与国家人口动态监测数据以及百度迁徙的相关数值[35,36]相较，产生了北京城市人口迁移与演变趋势下人口流动变化趋势特征的一致性重要结论。这在一定程度上反映出我国首都与其它各城市之间的人口迁徙和演变趋势。且进一步分析可得如下结论：(1)于纵观维度观测，中国首都与各个城市之间的人口流动网络具备类小世界性的属性；(2)从横向流动的层面统计，以首都为核心的主要城市之间人口整体流动数值满足幂律分布的规律。

值得一提的是，鉴于户籍政策问题等可能性原因，北京城市人口流动变化净增加值多年来持续处于“较多”等级，而不是“多”等级的水准区间内运行。