矩阵型灰色关联度的特征检验方法及其应用

刘 震，谢玉梅，党耀国

(1.江南大学 商学院 金融创新与风险管理研究基地，江苏 无锡 214122; 2.南京航空航天大学 经济与管理学院，江苏 南京 211106)

0 引言

灰色关联是灰色系统理论的一个重要分支，其基本思想是利用线性插值将离散数据映射为连续折线，进而通过几何特征相似程度判别序列间关系[1]。相对于一般的相关性分析方法，灰色关联模型将数据间关系视为不确定的灰色特征，在统计规律不明确的情况下仍然有较好的分析效果[2]，因此在目标识别、农村经济、绩效评估等领域得到了广泛的应用[3～5]。邓氏关联度是灰色关联模型的最初始形式[6]。众多学者在此基础上进行改进，提出了B型关联度[7]、C型关联度[8]、T型关联度[9]、斜率关联度[10]等。此后，刘思峰以整体积分形式构建了广义灰色关联模型[11]，并且提出了接近性和相似性的分析思路[12]。

近年来，面板数据、矩阵数据和高维场数据成为灰色关联的热点方向[13]。张可提出了面板数据灰色关联的概念，由于面板数据在模型中呈现矩阵形式，因此也被称为矩阵型灰色关联模型[14]。王正新以邓氏点系数灰色关联模型为基础，构建了基于时间、指标、方案的三维灰色关联模型[15]。钱吴永利用“水平”、“增量”和“变异”信息对面板数据进行降维，构建了基于多指标面板数据的灰色矩阵关联分析模型[16]。刘震提出了空间网格的概念，并且基于相似性和接近性构建了的两类面板数据灰色关联模型[17,18]。崔立志定义面板数据的矩阵表现形式，构建了针对面板数据的灰色矩阵相似关联度模型[19]。

在灰色关联模型中，几何特征差异性的量化方式主要有两种，一种是计算关联系数后再进行整合，另一种是利用积分直接识别序列间的面积或者体积。虽然两种计算方式不同，但本质上都是利用算数平均计算两序列间的平均差异。这种平均化的计算结果有助于我们了解变量间的总体关系，但同时也损失了一些差异性信息，例如时间维度下变量关系的变化趋势，以及样本间关系的稳定性判断。针对这一问题，Liu提出了一元灰色关联度的稳定性与趋势性检验方法[20]。但是该方法只能作为一元时间序列灰色关联度的补充分析，无法处理矩阵型灰色关联分析结果。

针对这一问题，本文尝试对矩阵型灰色关联模型进行优化，利用行为矩阵差值定义特征差异矩阵，构建基于矩阵2范数的多元灰色关联模型。接着以特征差异矩阵为研究对象，利用变异系数基本结构定义稳定性系数，利用最小二乘法推导趋势性系数，提出矩阵型灰色关联度的特征检验方法，以期为矩阵型灰色关联模型提供补充分析。最后，将矩阵型灰色关联模型及其特征检验方法应用于湖北省恩施州的长期多维贫困分析，通过与现有方法的对比验证模型有效性，进而分析恩施州8个市县的实际贫困情况，并且利用特征检验方法分析各地区贫困的不确定性和趋势性。

1 矩阵型灰色关联模型的优化

矩阵型灰色关联是经典一元灰色关联模型在三维空间中的拓展，主要分析行为矩阵间的相关性问题。行为矩阵的概念与行为序列类似，都是反映研究对象行为特征的一组变量，不同的是行为序列表现为向量，而行为矩阵表现为矩阵[1]。假设系统对象i在点(s,t)处的行为值为xi(s,t)，s=1,2,…,m，t=1,2,…,n，则行为矩阵可以表示为

观察行为矩阵可以发现，Xi包含两个维度。当其中一个维度为截面数据，另一个维度为时间序列时，行为矩阵也被称为面板数据。行为矩阵是度量序列几何特征的基本单位，通过对比几何特征之间的差异可以判别行为矩阵之间的关系。这种量化方式十分直观，但也存在一些问题，随着数据维度的增加，模型计算量将会呈现几何级数增长。为此，本文尝试从矩阵的角度直接对矩阵型灰色关联模型进行优化。

灰色关联理论要求建模前对原始矩阵进行初始化处理，避免量纲或者数量级对于结果的干扰。矩阵型灰色关联模型同样如此，根据处理问题的不同，常见有始边零化象算子、区间化算子、均值化算子等。初始化后的行为序列表示为XiD，行为值为xid(s,t)。很多学者对初始化算法进行了专门的研究，本文不再赘述[21,22]。需要注意的是，为了表达方便，本文直接用Xi表示初始化后的行为矩阵。

定义1已知两组行为矩阵Xi与Xj，i,j为系统标号，令rij(s,t)=xi(s,t)-xj(s,t)，则称

(1)

为矩阵Xi与Xj的特征差异矩阵。

由于Xi与Xj均为初始化后的行为矩阵，因此两者之差体现了行为矩阵之间的几何特征差异。根据灰色关联基础理论可知，特征差异越大，两行为矩阵之间的关系越小；特征差异越小，两行为矩阵之间的关系越大。为了度量特征差异矩阵的大小，引入矩阵范数对特征差异矩阵进行量化。

定义2已知特征差异矩阵Rij，则称

(2)

为矩阵型灰色关联度。

矩阵范数是矩阵论、线性代数、泛函分析等领域中常见概念，以2范数的应用最为广泛。在公式(2)中，‖Rij‖2即为2范数，表示特征差异矩阵Rij的欧几里德长度，计算公式为

2 矩阵型灰色关联度的特征检验方法

矩阵运算的形式有效降低了多维灰色关联模型的计算需求，但本质上仍然是对于行为序列整体相关性的判断，无法估计结果的可靠性[23]。为了更加深入的进行数据信息挖掘，考虑从数据关系的稳定性和趋势性视角对矩阵型灰色关联度的特征进行检验。

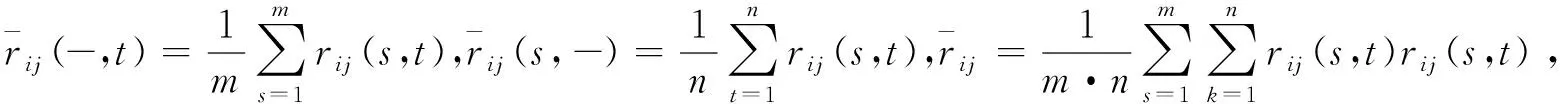
(3)

为第一维度稳定性系数，

(4)

为第二维度稳定性系数，

(5)

为总体稳定性系数。

由于矩阵型灰色关联模型的特征差异矩阵具有两个维度，因此关联度稳定性的评估从横向、纵向和整体三个方面展开。三类稳定性系数的基本结构一致，采用变异系数形式体现特征差异矩阵的波动情况，避免了数量级对于结果的影响。

稳定性系数越大，灰色关联度的稳定性越低。稳定性系数认为，特征差异矩阵在某一维度或总体上波动较大时，关联度并不稳定，此时稳定性系数计算结果较大。同时，稳定性的度量还要考虑关联度的约束。当关联度较大时，序列间相关程度理应相对稳定，判断标准应该更加严格；当关联度较小的时候，稳定性判断标准可以适当宽松，稳定性系数可以适当调低。根据这一原理，在分母位置加-ln|γij|入起到调节作用。具体而言，当|γij|→1时，-ln|γij|→0，轻微的波动也会造成稳定性系数趋向于正无穷；当|γij|→0时，-ln|γij|→+∞，即使特征差异矩阵波动，稳定系数也会等于零。

当行为矩阵在某一维度为时间序列时，继续进行趋势性检验。首先建立估计趋势性评估的基本形式，设第一维度的趋势性评估基本形式为

rij(s,t)=a(-,t)s+b(-,t)

(6)

第二维度的趋势评估基本形式为

rij(s,t)=a(s,-)t+b(s,-)

(7)

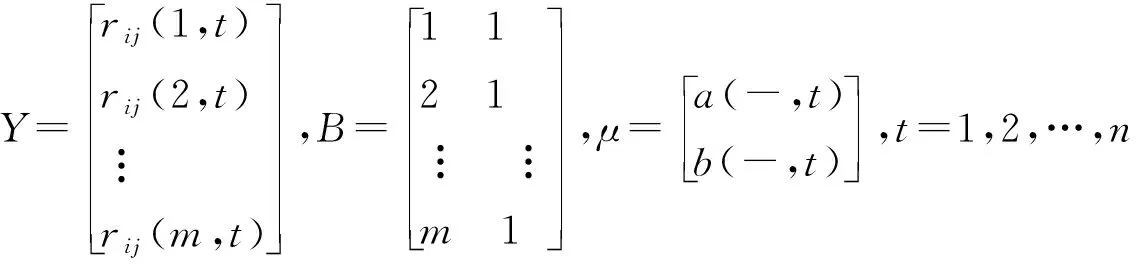
第二维度的最小二乘参数估计满足

定义4已知特征差异序列Rij，令

(8)

趋势性系数本质上是对特征差异序列变化趋势的量化。当特征差异序列在某一维度上逐渐增大时，最小二乘估计系数为正，系数越大表明趋势越明显。特征差异越大说明序列间相关性越低，因此趋势性系数为正表示序列间关系有减小的趋势。反之，趋势性系数为负表明相关性逐渐增大。系数绝对值表示变化趋势的强弱。

为了更加直观的表达特征检验结果，稳定性和趋势性系数可整理如表1所示。

3 基于灰色关联理论的恩施地区长期多维贫困分析

恩施土家族苗族自治州(简称恩施州)位于湖北省西南部，地处鄂、湘、渝交汇处，以山地为主要地貌。当地自然资源丰富，森林覆盖率接近70%，但也面临着地形复杂、基础设施落后、人口素质低、医疗卫生条件较差、自然资源难以转化的困境。恩施1983年8月19日建州，下辖恩施、利川2个县级市，建始、巴东、宣恩、咸丰、来凤、鹤峰6个县，经济发展较为落后，是我国西部大开发的重要地区，也是典型的“老、少、边、穷”地区。恩施州农村和少数民族人口居多，贫困与返贫现象较为严重。2010年《中国农村扶贫开发纲要》将湖北恩施列为国家重点扶持的集中连片特困地区，2011年湖北省成立了武陵山少数民族经济社会发展试验区，也把恩施州整体纳入发展规划[24]。

长期多维贫困是近年来反贫困领域的一个热点研究方向。不同于传统的一维静态收入贫困，长期多维贫困以一段时间内的总体贫困为标准，评估结果更加客观，但是评估体系也更加复杂。为此，本文采用矩阵型灰色关联模型对恩施州2市6县的贫困状态进行评估，同时与现有方法进行对比。借鉴已有的研究成果、数据可获取性以及恩施地区实际情况，构建多维贫困指标体系如表1所示。指标体系包含4个维度8个指标，分别从经济发展、人民生活、环境资源、健康教育四个方面刻画了区域贫困情况。

根据表1指标体系，本文收集了2013～2017年恩施州2市6县的面板数据。其中人均GDP和人均收入来源于wind数据库，用水普及率来源于恩施州统计年鉴，其余指标需要换算，财政收入占支出比、人均存款、人均耕地面积基于wind数据库得出，万人医生数量和百名小学生教师数量是查询恩施州统计年鉴相关数据后计算得出的。相关指标的描述性统计如表2所示。可以发现，经济发展与人民生活指标总体呈上升趋势，但是环境与资源、教育与健康指标出现了不同程度的波动，并且多数指标的标准差在时间维度上有所增加，体现了各县市间的差距正在拉大。

表1 多维贫困指标体系

表2 多维贫困指标的描述性统计

由于本文数据的量纲与数量级具有较大的差异，因此选用均值化算子在时间维度上对原始数据进行初始化。设原始数据为xi(s,t)，i表示恩施州的8个县市，s表示多维贫困指标，t代表数据年份，则

(9)

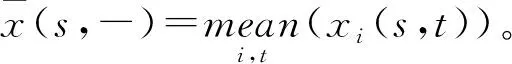
数据初始化后，利用各个县市在每个时间节点和指标下的最大值构建最优矩阵

(10)

并且以各指标平均值上下浮动15%,5%,-5%,-15%为标准构建基准矩阵。各矩阵分别与最优矩阵计算灰色关联度。当某县市的灰色关联度大于15%基准关联度时，认为该地区的多维贫困情况为优；当某县市的关联度大于5%小于15%基准关联度时，该地区多维贫困情况为良；当某县市的关联度大于-5%小于5%基准关联度时，该地区多维贫困情况为中；当某县市的关联度大于-15%小于-5%基准关联度时，该地区多维贫困情况为差；当某县市的关联度小于-15%基准关联度时，则说明该地区多维贫困情况恶劣。由此得到多维贫困分级评价标准，如表3所示。在此标准下，总结恩施州8个县市的长期多维贫困评价结果如表4所示。

表3 恩施州长期多维贫困的灰色关联分级评价标准

表4 恩施州长期多维贫困的灰色关联评价结果

为了验证评估的准确性，采用多维贫困测量中最常用的AF计数法(Alkire & Foster Counting Measurement)[25,26]作为对比模型。AF计数法是Alkire和Foster于2011年提出的一种通过计数手段实现多维贫困测量的方法，在测量长期多维贫困中使用三个临界值，即贫困指标临界值、贫困维度临界值和贫困持续期临界值，通过这三个临界值依次确定各评价对象在指标维度上是否贫困，在维度数量上是否贫困，在持续时间上是否贫困，详细步骤参考文献[27～29]。在本文算例中，贫困指标临界值设定为表2中各指标的均值，贫困维度临界值设定为4，贫困持续期临界值设定为2.5，据此可得结果如表5所示。

表5 恩施州长期多维贫困的AF计数法评价结果

在表5中，第一行“是否贫困”为AF计数法对于恩施州各市县长期多维贫困状态的判断，第二行“长期多维贫困指数”表示贫困状态所占比例，第三行“长期多维贫困距”表示贫困深度。由于灰色关联评估方法是基于恩施州各市县指标绝对值做出判断，与长期多维贫困距的评价目标类似，因此将灰色关联评估结果与多维贫困距进行对比，如图1所示。由于灰色关联与多维贫困距在评价结果中的数字含义相反，灰色关联度越大说明贫困程度越低，而多维贫困距越大说明贫困程度越高，因此图1对关联度进行了倒数处理。

图1 灰色关联度评估结果与多维贫困距

观察图1可以发现，灰色关联与AF计数法的评估曲线基本一致，均判定恩施市的长期多维贫困程度最低，宣恩县的长期多维贫困情况最为严重，这说明了本文模型的有效性。需要指出的是，鹤峰县的长期多维贫困状况在两类评估方法中均属于较为严重的状态，但是在表5中AF计数法却将鹤峰县划分为非贫困状态，这显然是不合理的。其原因主要是AF计数法存在三重临界值，忽略了指标偏离程度对于评估结果的影响，同时当指标取值在临界值附近时很容易造成结果偏差。这也在一定程度上说明了灰色关联模型在长期多维贫困评估中的优势。

接下来，采用灰色关联模型进行长期多维贫困的分维度评估。同样以指标平均值上下浮动15%,5%,-5%,-15%为标准，对恩施州8县市的4个贫困维度进行评价，结果如表6所示。从中可以发现，恩施州各市县在资源环境上总体表现良好，反而是总体评价最高的恩施市在资源环境上得分偏低。健康教育总体水平不高，只有恩施市和来凤县达到了良的水平。经济发展的差距较大，只有恩施市达到了优的水平。人民生活有一定的差距，建始县和咸丰县仍然处于差的状态。

表6 恩施州各维度长期贫困的灰色关联评价结果

对恩施地区多维贫困灰色关联评估结果进行特征检验，从总体和四个贫困维度计算稳定性系数和趋势性系数，如表7和表8所示。从表7中可以看出，鹤峰县的稳定性系数最高，这说明鹤峰县的多维贫困不确定性较大，这种不确定性体现在指标维度与时间维度中。恩施市的稳定性系数最低，说明恩施市的贫困不确定性较低。在表8的趋势性系数中，系数为负说明该地区的多维贫困呈现减缓的态势，系数为正说明该地区的多维贫困正在恶化。建始县是多维贫困恶化最明显的地区，尤其是资源环境的恶化需要关注。来凤县是多维贫困减缓最明显的地区，经济发展是其中最主要的动力来源。

表7 恩施州长期多维贫困的稳定性系数

表8 恩施州长期多维贫困的趋势性系数

总结恩施州八县市的多维贫困评价结果，包括灰色关联度、稳定性系数和趋势性系数，如图2所示。对比发现，多维贫困程度与多维贫困发展趋势之间没有直接联系。在所有八个市县中，恩施的多维贫困情况最为良好，稳定性系数也是最低，但是有贫困加深的趋势。宣恩县的多维贫困情况最为严重，同时有贫困加深的趋势，需要引起重视。鹤峰县多维贫困评价较差，同时稳定性系数也最高，说明该地区的致贫不确定性因素较多。

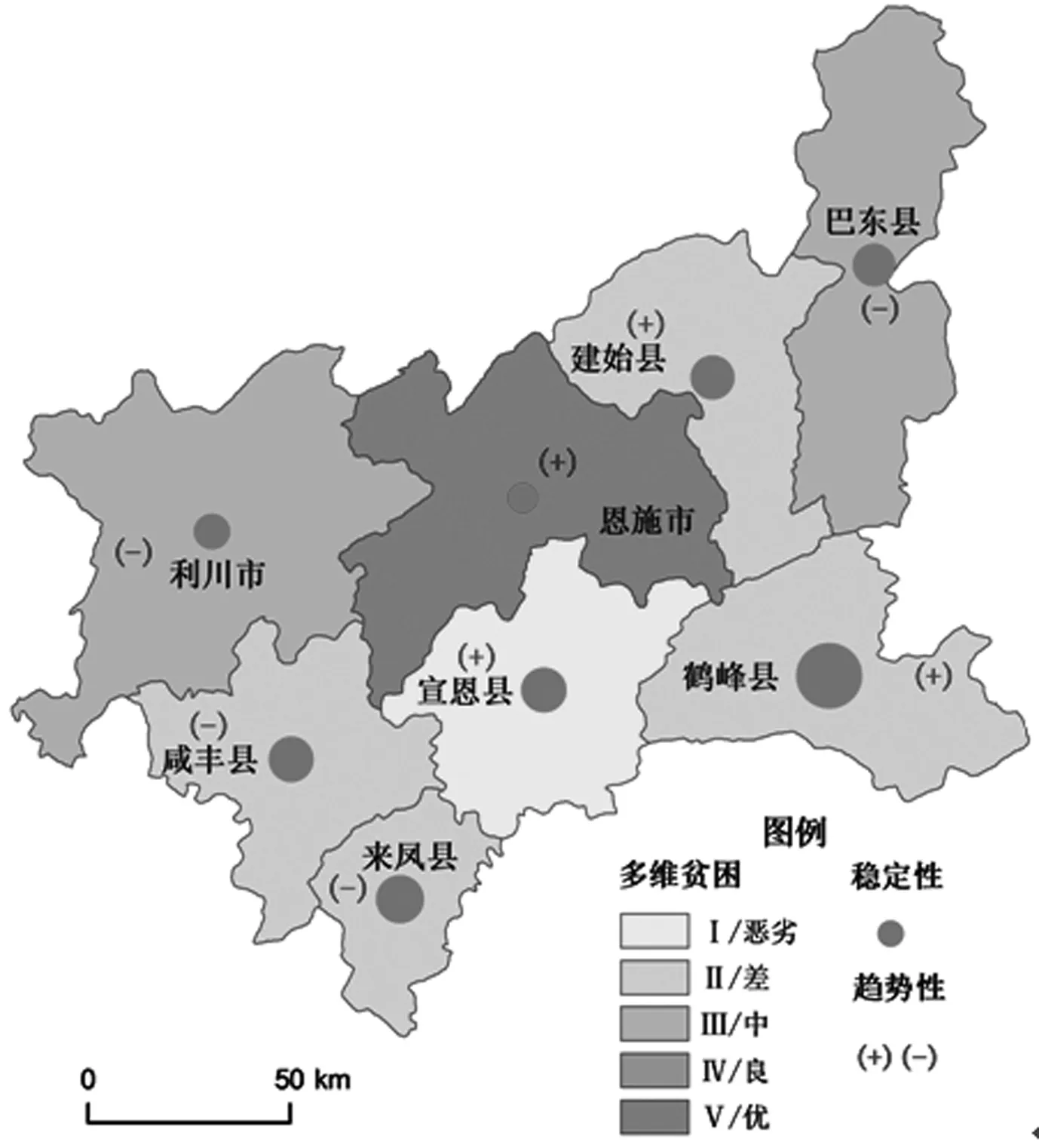
图2 施恩州长期多维贫困分析

进一步总结施恩州八个市县各多维贫困子系统的情况，分为经济发展维度、人民生活维度、资源环境维度和健康教育维度，如图3所示。对比灰色关联度、稳定性系数和趋势性系数，发现三者之间仍然没有直接联系。在经济发展维度中，各市县贫困程度较高，有6个市有恶化的趋势。在人民生活维度中，评价结果为优的城市较多，多数城市的人民生活水平正在逐渐改善。在资源环境维度中，只有施恩市的评价结果为差，其余城市的评结果都为优，所有城市的资源环境都在改善，只是一些城市发展的稳定性较差。在健康教育维度中，施恩州8个市县的评价普遍较低，3个市县仍然有恶化的趋势，这说明健康教育是施恩州多维贫困的一项短板，需要大力推动教育扶贫与医疗扶贫的强度。

图3 施恩州长期多维贫困子系统分析

4 结语

灰色关联的检验方法与检验准则是灰色关联理论的重要发展方向。现有灰色关联检验方法尚处于起步阶段，仅能处理一元灰色关联问题，因此本文构建了矩阵型灰色关联模型的检验方法。具体而言，本文的创新点主要体现在两个方面：(1)对矩阵型灰色关联模型进行改进，采用矩阵2范数构建了新的灰色关联度计算公式；(2)在特征差异矩阵的基础上，提出了矩阵型灰色关联度的特征检验方法，并且从稳定性和趋势性视角构建了检验系数。

在应用方面，矩阵型灰色关联模型被应用于恩施州8个市县的长期多维贫困评估。在与AF计数法的对比中，灰色关联模型与AF计数法的评估结果基本一致。甚至在某些市县中，灰色关联模型相较于AF计数法更加准确。同时，矩阵型灰色关联模型的特征检验方法对长期多维贫困评估进行了补充，有效分析了恩施州8个市县长期多维贫困的不确定性以及发展趋势，验证了本文模型的有效性与实用性。

当然，本文方法也存在一些不足。首先在模型方面，关于矩阵型灰色关联模型及其检验方法的研究仍然处于起步阶段，本文仅针对一般的面板数据的情况进行了讨论，未来可以将研究进一步拓展到高维场数据或者一些特殊的面板数据，例如非等间距或有缺失值的面板数据。其次在模型的应用中，由于统计资料的限制，文章的多维贫困指标体系纳入一些间接性指标，希望在未来的研究中能够进一步优化，同时灰色关联方法与AF计数法在多维贫困分析中的对比也需要进一步研究。