基于概率语言BWM与PROMETHEEII的多准则决策方法
耿秀丽,周青超
(上海理工大学 管理学院,上海 200093)
0 引言
由Brans[1]提出的偏好顺序结构评估法(PROMETHEE),是一种建立在“级别高于关系”的多准则决策方法,该方法过程简单、计算简便、意义明确,对环境具有灵活性和适应性。在决策过程中,每一个备选方案的各个准则值都要求与其他备选方案的各个准则值进行比较,使得各备选方案间都得到了充分的比较,保证了排序结果的稳定性与可靠性。PROMETHEEI通过方案的流入量和流出量建立方案间的部分偏好关系,PROMETHEEII通过方案的净流量建立方案间的完全偏好关系。PROMETHEE广泛应用于各个领域,文献[2]将PROMETHEE用于商业小额贷款信用评级,文献[3]将PROMETHEE方法应用于FMEA风险评估,文献[4]将PROMETHEE方法用于确定失效风险排序,文献[5]将PROMETHEE用于城市防洪减灾方案的优选。但上述文献中PROMETHEE方法都只处理了定量的信息,而评价信息往往存在模糊性和不确定性。
针对多属性决策中评价信息的模糊性和不确定性问题,模糊数常用来处理评价信息。文献[6]用三角模糊数来处理PROMETHEE中的评价信息,文献[7]用灰度数来处理PROMETHEE中评价信息的模糊性,文献[8]用二型模糊数来处理PROMETHEE中的评价信息。但使用单一语言术语的模糊语言不能准确的表达专家的观点。犹豫模糊语义术语集合(Hesitant Fuzzy Linguistic Term Set, HFLTS)可以同时使用多个语义术语来表达专家的意见。文献[9]使用犹豫语言模糊集来处理PROMETHEE中的评价信息,能够很好的表现出专家在决策过程的犹豫性。但在某些具有大量不确定因素的决策问题中,专家对语义集的偏好程度不同,而HFLTS中的语义集被赋予相同的权重,所以会造成专家偏好信息的损失。因此,Pang等[10]在HFLTS的基础上提出了概率语言术语集(Probabilistic Linguistic Term Set, PLTS)。概率语言集中的语义集被赋予了相应的概率,可以体现出专家的犹豫偏好程度,能够比较准确的表现出专家的偏好信息。本文采用PLTS表达专家对备选方案的评价信息,将概率语言形式的评价信息纳入PROMETHEE II中对备选方案进行排序。
传统的PROMETHEE 也存在准则权重需要从外部获得的问题,针对准则的权重要从外部获得的问题,文献[11,12]采用AHP改进PROMETHEE方法来确定准则的权重,对于n个准则的权重问题,AHP需要n(n-1)/2次比较,两两成对比较虽然保证了打分的全面性,但过程复杂繁琐,且当准则数量较多时不容易满足一致性要求。荷兰学者Razaei[13]提出了最优最劣法(Best-worst Method, BWM),其思路是通过筛选最优和最劣两种特殊准则,将其他准则分别与最优准则与最劣准则进行比较,实际只进行(2n-3)次比较,简化了比较过程,也保证了结果的可靠性,所以在决策领域得到了广泛的运用,文献[14]将BWM用于可持续供应商的选择;文献[15]通过建立新的模型,并将M1模型与M2模型进行比较分析,提出了用BWM解决群决策方法;文献[16]将BWM应用于应急决策的选择。本文将BWM和PROMETHEE II方法相结合解决多属性决策问题,并将概率语言纳入BWM方法中来确定准则的权重。
综上,本文提出了基于概率语言BWM与PROMETHEE II的多准则决策方法,采用概率语言表达专家给出的语义评价信息和准则之间的影响关系。将概率语言纳入BWM中计算出各准则的权重,再将概率语言作为评价语言纳入PROMETHEE II中对备选方案进行排序。最后,将本文所提方法应用于无人机改造方案,并进行对比分析,验证所提方法的有效性。
1 理论知识
1.1 概率语言术语集的基本概念
2016年Pang等[10]提出概率语言术语集,概率语言术语集是由语义集和语义集相对应的概率组成的语义集合,L(P)为专家用概率语言术语集表达的语义评价信息。概率语言术语集不仅可以表达专家在方案评估时犹豫不定的情形,还可以表现出专家的偏好程度,相比其他语义评价方法能避免评价过程中专家偏好信息的损失[10]。
定义1[17]设S={s0,…,sα}为LTS,一个PLTS可以被定义为:
L(p)={L(x)(p(x))|L(x)∈S,
(1)
其中,L(x)(p(x))表示语义集L(x)的概率为p(x),#L(p)是所有L(p)中包含的语义集的个数。
如设LTS为五个粒度的语义术语集,S5=(S0=VL,S1=L,S2=M,S3=H,S4=VH)。当准则为无人机的续航时间(C3)时,专家给出“大多时候对方案影响很大,但有时影响不大”,则此时记“大多时候对方案影响很大”为S4,其概率为0.7,记“有时影响不大”为S1,其概率为0.2,此时的={(S1,0.2),(S4,0.7)}。

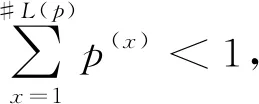
(2)

定义3[17]设L(p)={L(x)(p(x))|x=1,2,…,#L(p)}为一个PLTS,r(x)为语义集L(x)的下标,则L(p)的得分函数如下:
(3)

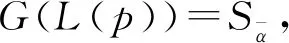
(4)
设概率语言术语集L(p)1和L(p)2的得分函数为G(L(p)1)和G(L(p)2),偏差度分别为σL(p)1和σL(p)2。当G(L(p)1)=G(L(p)2)时,如果σL(p)1<σL(p)2,则L(p)1>L(p)2;如果σL(p)1=σL(p)2,则L(p)1=L(p)2;如果σL(p)1>σL(p)2,则L(p)1 定义5[18]设S={s0,…,sα}为LTS,L(p)={L(x)(p(x))|x=1,2,…,#L(p)}为一个PLTS,r(x)为语义集L(x)的下标,L(x)中语义集L(x)的粒度越大,表示评价时的犹豫度越大,则L(p)的犹豫度如下: (5) 定义6[18]设L(p)={L(x)(p(x))|x=1,2,…,#L(p)}为一个PLTS,则L(p)转化为精确数值的转化函数如下: (6) 概率语言术语集L(p)随着L(p)越大而越优,偏差度的越小而越优,犹豫度的越小而越优。 传统的BWM方法,进行专家打分时用1~9个刻度进行打分,但评价信息具有犹豫性和不确定性,并且决策信息包含概率信息,故采用概率语言进行评价,保证了评价信息的准确性。如设PLTS为9个粒度的术语集,L(p)={(S0,0.8),(S4,0.1)}表示为“大多时候准则Ci极端优于准则Cj,有时准则Ci稍微劣于准则Cj”,具体的粒度表示如表1。通过将概率语言与BWM相结合,求解各准则的权重,其具体步骤如下: 步骤1在准则集{C1,C2,C3,…,Cn}中选取最优准则CB和最劣准则CW。 步骤2经专家讨论用概率语言进行评价,确定最优准则CB相比于其他所有准则Ci的偏好程度,构建比较向量AB=(aB1,aB2,…,aBn),其中aBi代表最优准则CB与其他准则Ci相比的偏好程度。 步骤3同理,确定其他所有准则Ci相比于最劣准则CW的偏好程度,构建比较向量Aw=(a1W,a2W,…,anW),其中aiW表示其他准则Ci与最劣准则CW相比的偏好程度。 minξ wj≥0,forallj 显然, 变换矩阵(A-μB)-1B的最大特征值将对应于原广义矩阵特征值方程中最靠近偏移值μ的特征值, 这个变换过程通常称作shift-and-invert算法[6]. 标准矩阵特征值问题可以采用隐式重启Arnoldi方法求解最大幅值的特征值, 在MATLAB软件中对应于eigs函数调用. (7) 将概率语言与PROMETHEE II进行有效的融合,确定概率语言在PROMETHEE II中的粒度,如设9个粒度的术语集,L(p)={(S2,0.8),(S4,0.2)}表示为“大多时候备选方案Xi在准则Cj上评价值高,但有时评价值稍高”,具体粒度表示如表2所示,利用BWM求得准则权重,结合PROMETHEE II对方案进行排序,具体步骤如下。 步骤1经专家组讨论,给出方案Xi在属性Cj下的评价值为fj(Xi),评价值用概率语言进行表示,构建决策矩阵。 步骤2通过公式(4)~(6)将概率语言术语转化为精确数值。 步骤3确定每个准则的偏好函数Pj(Xi,Xs)。准则偏好函数有两个要素:dj和Pj(Xi,Xs)。其中dj=fj(Xi)-fj(Xs),表示方案Xi和Xs在准则j上的准则值之差;Pj(Xi,Xs)=Pj(fj(Xi)-fj(Xi))=Pj(dj),Pj(Xi,Xs)∈[0,1]是偏好函数值,表示从准则j的角度看,方案Xi比方案Xs好的程度。根据文献[1]选用常用偏好函数,具体函数如公式(8)所示。 (8) 步骤4确定方案两两比较的优先指数π(Xi,Xs)。π(Xi,Xs)是决策者同时考虑所有的属性时,对方案Xi与Xs的优先强度的描述,其中公式(9)中的准则权重wj,本文已通过概率语言与BWM相结合求得。 (9) 步骤5确定方案Xi的流出量Φ+(Xi)如公式(10)所示,Φ+(Xi)表示方案Xi级别优于其他方案的可能性,其值越大方案Xi越优。 (10) 步骤6确定方案Xi的流入量Φ-(Xi)如公式(11)所示。Φ-(Xi)表示其他方案级别优于Xi的可能性,其值越小方案Xi越优。 (11) 步骤7确定方案Xi的净流量Φ(Xi)如公式(12)所示。然后对备选进行方案排序,净流量越大,证明备选方案越好。 Φ(Xi)=Φ+(Xi)-Φ-(Xi) (12) 表2 PRPMETHEE II中概率语言1~9粒度具体说明 经专家组讨论,得出续航时间(C3)为最优准则,防水性能(C1)为最劣准则,采用概率语言术语对准则间的比较进行评价,通过将最优准则C3与其他准则Ci进行对比,得出与各准则的比较值如表3所示。同理,将最劣准则C1与其他准则Ci进行对比,得出与各准则的比较值如表4所示。 表3 最优准则与其他准则的比较值 表4 最劣准则与其他准则的比较值 利用公式(3)~(6)将表3与表4的概率语言评价信息通过函数转化为精确值,得到精确值评价表,分别如表5和表6所示。 表5 将表3概率语言评价值转化为精确值 表6 将表4概率语言评价值转化为精确值 通过数学模型(7),使用MATLAB求得各准则的权重,如表7所示。 表7 各准则的权重值 经过专家组讨论,得到每个方案在每个准则上的评价值并用概率语言表示,如表8所示。并通过公式(3)~(6)通过函数将概率语言术语转化为精确值,如表9所示。 表8 专家组给出的概率语言方案评价信息 表9 方案的概率语言术语评价信息转化为精确值 根据PROMETHEE II的排序方法,利用公式(8)~(10),分别求出每个方案的流出量Φ+(Xi)与流入量Φ-(Xi),再通过公式(11)求出每个方案的净流量Φ(Xi)。 表10 方案的流出量、流入量、净流量 通过计算,得出了每个方案的流出量Φ+(Xi),流入量Φ-(xi)与净流量Φ(xi),如表10所示。得到了改装无人机方案的完全排序结果为X1>X4>X5>X2>X1。所以应该选择第一种方案对无人机进行改造。 文献[19]采用AHP-PROMETHEE方法来对方案进行排序,采用本文案例的数据,用文献[19]所提方法进行计算,与本文方法进行对比。首先将概率语言与AHP相结合,通过之前的数据,构建专家评价矩阵如表11所示。 表11 AHP评价矩阵 根据表格可以看出AHP的比较次数为25次,而本文所使用的BWM只需要7次比较。通过公式(3)~(6)将评价矩阵中的概率语言转化为精确值,如表12所示。再利用MATLAB计算得出各准则权重分别为w1=0.0756,w2=0.0372,w3=0.4050,w4=0.1398,w5=0.3425。与BWM中求出的准则权重排序一致,根据表7与表8,利用公式(8)~(11),求出方案的流出量Φ+(xi),流入量Φ-(xi)与净流量Φ(xi),如表13所示。得出的排序结果为X1>X4>X5>X2>X1。对比方法与本文所提方法计算结果排序一致,但可以明显看出当指标值过多时,对比方法使用AHP求权重就显得尤为复杂,指标越多,成对比较的次数越多于BWM中的比较次数,所以当指标过多时,对比方法明显不适用。 表12 AHP评价矩阵中的概率语言转化为精确值 表13 利用AHP与PROMETHEE II结合得出方案的流出量、流入量、净流量 本文针对多准则决策问题提出了一种新的方法,所提的方法具有如下的特点: (1)将概率语言作为评价语言与BWM结合计算准则的权重,并且BWM法比较次数少于传统的的AHP法,因此所提方法即保证评价信息准确性与有效性,又保证了计算的方便性。 (2)选用PROMETHEE II法作为排序方法,避免了决策补偿性对决策排序的影响,同样选用概率语言作为评价信息,保证了评价信息的准确性。 所提方法已用于某企业改进无人机设计方案的评价分析,通过实证分析,验证了所提方法的有效性和可行性。本文考虑了备选方案准则权重的判定及排序,下一步还会进一步讨论多准则群决策的评价与分析。2 指标权重的求解及备选方案的排序
2.1 基于概率语言BWM权重计算方法
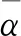


2.2 基于概率语言PROMETHEE II排序方法


3 算例分析











4 结论

