金属矿山企业生产计划优化方法
马 龙,卢才武,顾清华
(1.西安航空学院 经济管理学院,陕西 西安 710077; 2.西安建筑科技大学 矿山系统工程研究所,陕西 西安 710055)
0 引言
矿山企业生产计划的编制和优化效果对企业生产作业和资源回收利用有着重大的影响,特别是因目标函数的不同而产生明显的差异。目前国内外学者重点采用数学规划和智能优化算法进行建模和解算。如文献[1~4]采用混合整数规划方法,解算出金属矿山企业生产计划的编制方案;文献[5,6]采用0-1整数规划方法,构建了金属矿山企业生产计划模型;文献[7~9]分别采用粒子群算法、帝国主义竞争算法和鸽群-粒子群算法,对矿山企业长期生产计划进行优化求解;文献[10]采用禁忌搜索算法,对金属分布不确定的露天矿山企业生产计划进行优化求解,文献[11,12]分别采用粒子群算法和蜂群算法,对多金属矿山生产计划进行编制和求解计算,尽管这些优化方法应用较广,但大多是用传统的仿生进化算法对矿山企业生产计划模型进行优化解算;算法的开发和探索能力弱,收敛计算速度慢,易于出现早熟现象,这给矿山企业生产计划的编制和优化带来诸多困难。另外,研究成果中多数以净现值最大化为目标,约束条件较为复杂,在实际矿山生产领域通用性较差,且忽视了矿山生产作业单位投入成本对企业总体经济效益的影响。
量子进化计算是由Benioff和Feynman于1980年提出,该算法以其快速的计算性能、精确的求解效果引起学术界的广泛关注[13,14],主要应用在函数优化、组合优化等问题中,而利用量子计算与改进的仿生进化算法进行融合,对金属矿山企业的开采生产计划模型进行优化计算还研究较少。
因此,针对现有研究成果的不足之处,本文针对金属矿山企业生产计划优化方法的主要贡献如下:
(1)构建的模型将开采和运输的单位成本考虑在内,为精准核算金属矿山企业的经济利润提供条件。
(2)约束条件中增加了矿产资源利用率,有助于监测不同类型的矿石开采利用效果。
(3)利用进化速度因子和聚集度因子,对量子粒子群算法的惯性权重参数进行改进,满足该算法求解最大化与最小化问题的适应性。
(4)利用量子进化计算与标准的仿生进化算法的完美融合,解决了标准进化算法的计算速度慢、收敛结果误差大的问题。
(5)设计了双层可行域搜索策略,加固了仿生进化算法搜索可行解的效果。
(6)利用Lingo、Cplex软件、非线性规划方法和基本粒子群算法,分别对模型的求解速度与不同人工智能算法的求解速度进行优化计算与比较,突出了本文算法的可行性。
纵观上述研究成果,为了精细化考量金属矿山企业的生产任务和成本利润问题,建立企业生产计划优化模型,提出改进的量子粒子群算法(Improved Quantum Particle Swarm Optimization, IQPSO),实现了金属矿山企业的单位开采和运输成本的计算精度和效率。
1 矿山企业生产计划模型
1.1 生产计划编制原则
金属矿山企业生产计划编制时需要综合考虑矿山作业的地质条件、生产工艺、矿石品位以及开采矿量等多种复杂的约束条件,编制过程中考虑的约束条件不同而形成的生产计划具有较大差异,特别是考虑的约束条件数量较多时,会使企业在编制和优化生产计划时困难较大。因此多数金属矿山企业生产计划从配矿或排产的角度优化调整采区各出矿点或采场的备采量、计划期内的开采量、矿石品位和回采率等参数,达到生产计划期内企业下达的开采生产任务。
通常矿山生产作业的采场作为生产作业活动的最基本单元,在开采矿石之前,需要做探矿、钻孔、爆破等准备工作,然后通过回采作业完成矿石的开采和运输,编制计划的目的是将这些工作按照一定的时空顺序组合排列,从而使矿山企业投入的单位开采和运输成本最小,其编制生产计划的基本原则为:(1)生产作业能力均衡配置;随着矿山作业进尺的推进,不同的采场或出矿点与破碎站的距离逐渐增大,每个采场的出矿能力均会受到不同程度的影响,导致作业工期延误、出矿量少等情况,因此在编制矿山企业生产作业计划时需要综合考虑生产任务量与作业能力间的均衡平稳,保证作业期内各工序准时完成;(2)开采量与出矿总量的合理分配;矿山企业的生产任务量是由年度、季度、月度以及日任务量构成,它们之间是由上而下逐级细分、由下而上逐级实现,为了保证采场均匀出矿和连续作业的要求,必须保证计划期内各采场的开采量和出矿总量的分配制约关系;(3)矿产资源综合利用率;矿山企业的目标是实现投入产出比持续增加,因为日出矿量、品位和回采率等均会制约企业的经济效益。
矿山企业生产作业计划编制过程中,需综合考虑多种因素的平衡与制约关系,开采作业过程无论从生产工艺还是时空顺序上均是环环相扣,矿山企业生产部门需要根据自身实际生产能力及各采场的作业方式制定符合实际生产需要的回采、出矿生产作业计划。
1.2 矿山企业生产计划优化模型
1.2.1 模型构建假设前提
假设1作业计划期时间t,t=1,2,…,T,T表示在计划水平内的总开采周期数。
假设2对于富含不同物质元素的矿石开采量源自同一个采场,且现有采场开采之前,已完成探矿、钻孔等生产工序。
假设3铲运机或卡车的运力、采场至堆场的距离均为已知固定值,且在建模时可不予考虑。
假设4选厂的入选品位事先由生产工艺的需要而确定,且随之生产需要发生动态调整。
假设5矿石的开采只在一个固定的采场施工作业,且矿石开采的人财物资源均已知,且在建模时不予考虑。
假设6金属矿山企业年开采计划任务量与月开采的矿石数量任务已经确定。
1.2.2 金属矿山企业生产计划目标函数
金属矿山企业生产过程是对生产计划月矿石开采量的采运成本进行计算,由于矿山每日或每周的开采生产会在多个采场同时进行,而不同的采场受到矿床地质赋存条件和矿岩结构的影响,其矿岩富含的矿物元素不同,由此需要利用铲运机或卡车将富含不同元素的矿石从采场运输到堆矿场,方便后续选矿厂的选矿需求,但在开采进尺深度的影响下,出矿场与堆矿场之间的距离会出现差异,由此会产生不同的单位运输成本,建立的目标函数为[11]:
(1)
式中,ci表示采场i的矿石开采和运输的单位成本,元/吨;xi表示第i个采场的矿石开采数量,单位:吨,且i=1,2,…,n。
1.2.3 编制生产计划的约束条件
为了验证IQPSO算法优化求解金属矿山企业生产计划的可行性,本文主要从生产技术指标方面构建模型的约束条件表达式[11]:
(1)品位波动约束;由于矿床赋存条件的差异,不同采场开采的矿石品位会产生一定的波动性,应该通过配矿等手段来满足选矿厂入选的品位指标需要,否则开采的矿石作为废石被排岩处理,建立数学表达式为:
(2)
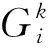
(2)生产计划期内开采矿石量;为了实现各采场出矿量的均匀出矿和连续采矿,建立的数学表达式为:
(3)
式中,Qmin,Qmax表示每个采场允许开采矿石量的界限范围(单位:万吨)。
(3)矿石开采总量的约束;在金属矿山企业生产计划期内,在短期开采生产计划期内,每月开采矿石数量任务是根据年开采生产计划任务的划分来确定的,开采的矿石量必须在规定开采总量范围内,建立的数学表达式为[11]:
(4)
式中,Q表示开采计划期内出矿的总数量(单位:万吨);δi表示采场的回采率(单位:%)。
(4)矿产资源综合利用约束;矿石回采率是评价矿山企业生产成本、企业管理水平和地质环境等指标的主要影响因素。因此,为保证矿山企业的持续生产作业和经营管理,需要考虑矿产资源综合利用约束条件,建立的数学表达式为:
(5)
式中,minδi,maxδi表示资源利用率的界限范围(单位:%)。
2 金属矿山企业生产计划优化与编制方法
2.1 基本的量子粒子群优化算法


(6)
(7)
式中:ω为惯性权重;c1,c2表示学习因子;c1,c2∈[0,1]。
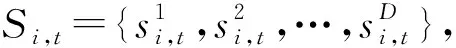
(8)
PSO算法中,通常取c1=c2,因此,式(3)可变为如下形式:
(9)
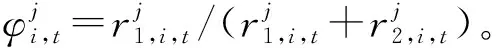
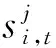
(10)
在搜索空间中的概率分布与位置更新是以薛定谔波动方程式和蒙特卡罗随机模拟方法为主,其数学模型分别为式(11)和式(12):
(11)
(12)
(13)
由上述量子粒子群的基本数学模型可知,该算法的进化过程计算为:
(14)
式中,ω表示惯性权重参数,取值如下:
(15)
(16)
2.2 算法参数优化
2.2.1 进化速度和聚集因子[11,19~21]

(17)
如果在实际问题中以极小值作为优化的目标函数,则可用下式(18)的进化速度因子:
(18)
在标准的量子粒子群算法中,算法求解计算问题的全局最优解时,种群内的粒子同样会向某个可行解区域不断的靠拢,但靠拢的粒子数量多寡,决定了问题求解的可行性,因此,利用聚集度因子来改变算法中的惯性权重参数是衡量算法收敛性能的重点。但是可以将种群内全部粒子的最优位置进行平均计算后,其算法的性能也会得到一定改善,计算所有粒子的当前最优位置如下:
(19)
(20)
(21)
式中,Jd∈(0,1],Jd值的大小,决定粒子的聚集程度。
2.2.2 改进的惯性权重
通常,算法中的惯性权重ω的取值大小与种群内粒子的最优位置呈现正相关,而与算法的收敛速度呈现反相关。因此,为了综合权衡惯性权重参数ω的合理取值,自适应惯性权重调整公式如下[11,18,20]:
ω=f(Sd,Jd)=ω0+ω1Sd+ω2Jd
(22)
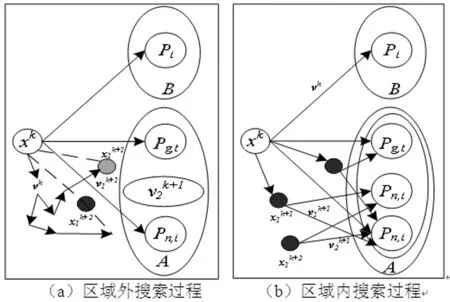
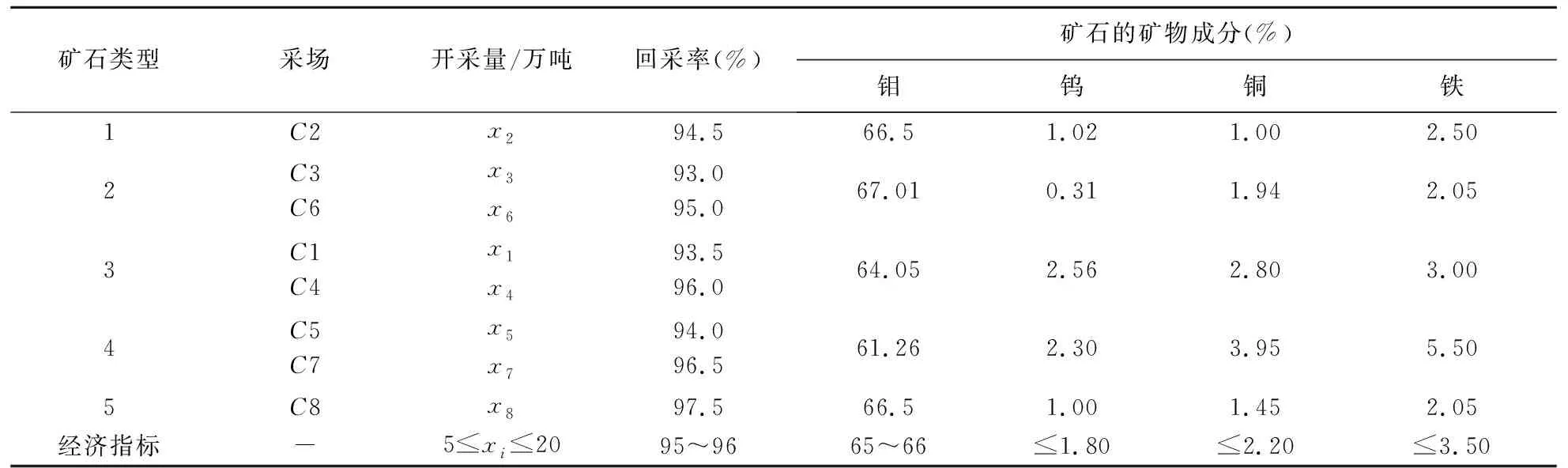
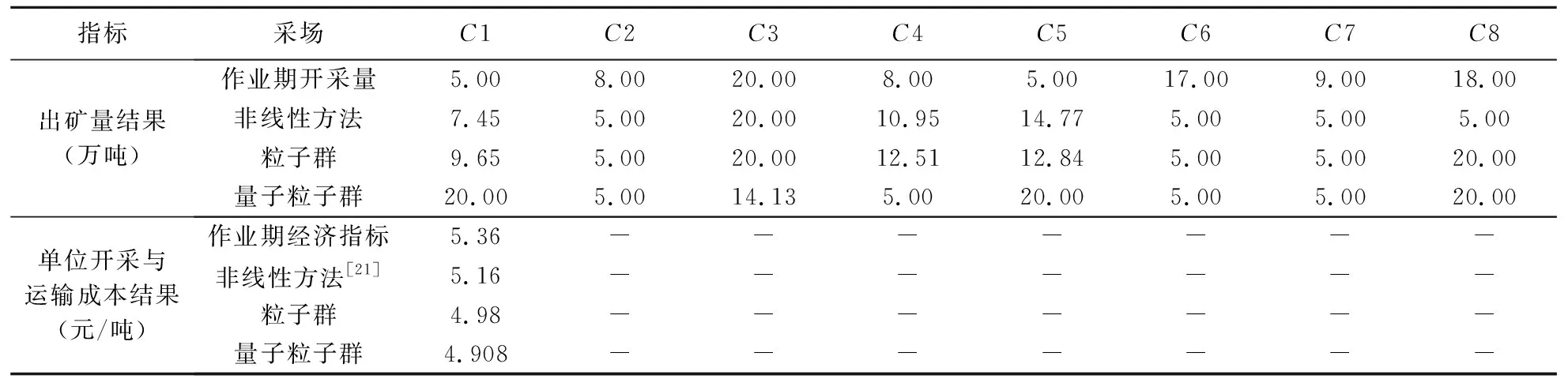
式中,ω0表示初始化惯性权重ω,取ω0=1;ω1表示赋予进化速度因子Sd的权重值;ω2表示赋予聚集度因子Jd的权重值,研究成果表明,ω1=0.9,ω2=0.4;0 2.3.1 生产计划模型处理策略 由于金属矿山企业生产计划模型求解会受到多种编制约束条件的影响,根据矿山企业精细化管理要求,构建以矿石开采和运输单位成本最小为目标的生产作业计划模型,该模型是一个具有品位、储量和开采率等严格约束的复杂问题,为了算法求解的便利性,利用惩罚函数的方法[22,23],将模型中的所有约束条件进行惩罚处理,处理后的约束条件模型如下: (23) 式中,φi(x)表示编制生产计划的约束条件模型中不等式项处理结果;φ(x)表示编制生产计划的约束条件模型中等式项处理结果;μ表示编制生产计划的约束条件中函数惩罚因子。 通过对金属矿山企业生产计划编制模型中的约束条件和目标函数进行惩罚处理后,转换后的优化目标问题的数学模型为: (24) 其中,violate(x)表示违反编制生产计划约束条件的等级程度;同时,violate(x)=0是算法搜索到最优解后可以满足的约束条件求解,violate(x)≠0是算法搜索到最优解后无法满足的约束条件求解,但整个粒子种群搜索到的最优解均可满足编制生产计划的约束条件。 2.3.2 双层可行域的粒子搜索策略 通过使用进化速度和聚集因子两个参数对量子粒子群算法进行优化后,种群内最优的个体粒子历史位置pi,t与群体历史位置pg,t是引导粒子飞行的方向标,将其进行加权平均换算后的位置值Si,t作为引导种群内其他粒子的飞行方向的吸引子,该吸引子作为决定整个种群可否进入搜索空间可行域内的关键参数。因此,为了进一步增加搜索空间外的粒子能够更多的进入可行域内,提升算法的搜索计算能力,提出了具有双层可行域的粒子空间搜索策略,使用该策略的基本想法是算法经过多次反复的迭代计算,种群内的个体粒子向最优位置靠拢时,不要参考粒子自身的最优位置值pi,t,只要与该粒子相关位置最近的可行域内的最优位置的个体粒子值pi,t不断靠拢,记为npi,t,pni(t)=(pni1,pni2,…,pniD),这样是为了让种群内尽可能多的粒子进入可行域内继续搜索计算[11],如图1所示。 图1 双层可行域搜索策略图 2.3.3 模型求解 根据上述生产计划编制原则来构建的生产计划模型与约束条件,要使用改进的量子粒子群算法求解计算,必须将种群内的粒子与模型内的变量X={xi,i=1,2,…,n}进行编码处理,这样可将不同采场内的矿石开采量作为生产计划优化问题的变量:min{f(x),xi∈X},并且为了更好地说明提出的算法与模型之间的映射关系,假设QPSO算法中的个体粒子分别表达了一种求解方案,维数表达为采场的数量,种群规模表达为采场的开采量,目标函数表达为算法的适应度函数,经过编码预处理后,模型的具体求解过程: 步骤2利用算法对生成计划模型进行反复迭代求解,若设定的迭代次数经过迭代计算后tmax与的取值一致,跳转至步骤(9)结束算法搜索计算过程,否则,跳转至步骤(3)继续执行。 步骤3根据种群粒子与可行域之间的位置关系,判断出目标函数的取值问题,若粒子处于双可行域内,则目标函数值为适应度函数值,否则,适应度函数值赋予无穷大。 步骤4根据种群粒子的适应度值,判断其优劣性,若当前粒子的适应度值比搜索到的最优位置pi弱,则将该粒子作为pi。 步骤5从单个粒子的最优位置pi中选取双可行域内距离该粒子最近的个体粒子作为聚集方向npi,t,记作pni。 步骤6根据双可行域内所有粒子的适应度值的优劣性,若当前粒子的适应度值比前一次计算的适应度值更优,对粒子的速度、位置、个体最优值、全体最优值和适应度值进行完全更新。 步骤7根据式(17)~(18)的关系,利用算法求解目标函数时的进化速度Sd,根据式(20)~(21)的关系,利用算法求解目标函数时的聚集度Jd,再根据式(22)求解出ω的值。 步骤8算法求解模型时,迭代次数t经过逐次增加后,跳转至到步骤(2)后再次判断。 步骤9模型求解结束,输出当前的全局最优位置值作为模型计算结果。 为了检验量子粒子群算法的改进效果以及用于求解金属矿山企业生产计划模型的可行性,以涵盖钨、钼、铜、铁等复杂矿物成分的某矿山区域的开采数据为例,其中,钨矿石的矿物成分以白钨矿为主,钼矿石的矿物成分以辉钼矿为主,铜矿石的矿物成分以黄铜矿为主,有时富含一定品位的可见斑铜矿成分,铁矿石的硫化物以黄铁矿成分为主,铁的氧化物以磁铁矿和褐铁矿成分为主[11,24]。经过对该矿山生产计划时期内的部分开采生产指标进行统计和分析后,假定在开采生产计划时期内有8个采场准备开采的矿石量为900000吨,且每种矿石由一个采场采出,具体的生产指标数据和作业计划数据分别见表1与表2所示。 针对上述构建的模型和算法,在配置为4GB内存,1.6GHz CPU的PC机环境下,利用 Matlab2015Ra平台,将给出改进量子粒子群算法中的惯性权重ω值为0.9,设定算法的迭代次数t=1000,初始种群规模为50,Sd=0.5,Jd=0.5;Lingo软件与Cplex软件的基本参数与文中生产计划模型之需的指定参数保持一致。 表1 矿物成分以及生产作业经济指标[11,20] 表2 开采矿石和运输矿石的单位成本 针对上述构建的模型和算法,依据式(23)和表1、表2的数据,对矿山企业开采和运输成本的计算结果,如图2所示。 图2 矿山企业开采与运输成本计算结果 图3 8个采场的矿石回采量分布图 根据图2的成本计算结果曲线分布状态可知,利用惯性权重参数的优化和双层可行域搜索策略对量子粒子群算法进行改进,并利用该算法对金属矿山企业生产计划模型中的采运的单位成本进行求解时,经过1000次的迭代计算,在迭代前50次时,开采和运输的单位成本值在5.1元/吨和5.4元/吨之间曲线波动较大,收敛速度较慢,鲁棒性较差;迭代到50到280次时,算法开始向开采和运输单位成本的局部最优值5.1元/吨平稳收敛,说明算法依然处于不断的寻优状态,而在300到600次时,算法受到双层可行域搜索策略的影响,可行域外的粒子开始迅速向可行域内的边缘靠拢,开采运输的单位成本从5.1元/吨向4.908元/吨的方向开始收敛,发生了一定的波动现象,但在600次以后,算法在单位开采运输成本为4.908元/吨的全局最优解上平稳收敛。 根据图3矿石开采量的雷达图清晰可知,以8个采场90万吨的基准开采矿量的初始分布结果为基础,利用3种算法对开采量为90万吨的矿石分布进行计算,采用非线性规划方法计算后,90万吨的矿石分布与基准开采分布结果较为接近,采用PSO算法求解计算后,采场C1、C2的开采量基本上与设定的基准开采矿量相同,而采场C6、C7的开采分布要明显低于基准开采矿量,只有在采场C3、C4内的开采矿量大于基准开采矿量,说明标准粒子群算法要比非线性规划方法好,但从总体上来看,这2种方法在开采矿量分布的求解结果差值较小。利用QPSO算法计算的8个采场的开采矿量分布较为均匀,而且开采矿量要比基准矿量明显增多,这是因为利用惩罚函数策略,将模型进行适当处理后带来的允许误差结果,并受到矿产资源开采利用的约束,使生产计划期内尽可能满负荷开采出更多的矿石。 为了检验模型与算法的求解速度,经过改进的量子粒子群算法解算出单位开采运输成本以及矿石开采量后,再次利用Lingo软件以及Cplex软件分别对文中的模型进行解算,其解算结果与文中算法一致,而经过解算后的模型求解时间却明显不同,从而可知模型的求解速度也发生明显变化,如表3所示。 表3 模型与算法的求解速度比较 为了比较出不同方法对于本文构建的生产计划模型的目标函数的求解效果,利用改进的量子粒子群算法求解获得的金属矿山企业生产计划中开采和运输成本的结果,如表4所示。 由表4的结果可以清晰地看出,该金属矿山企业在开采时期内的8个采场中的矿石开采量为90万吨,将生产作业期内预估计每吨矿石的单位采运成本5.36元作为其他方法求解的对比标准,比较出非线性规划方法[25]、标准粒子群优化方法和量子粒子群优化方法的求解结果,其计算结果分别为5.16元/吨、4.98元/吨、4.908元/吨,计算时间分别为32秒、23秒、15秒;虽然3种方法的优化计算结果差异较小,但不同方法的优化计算时间却明显不同,这是因为改进的量子粒子群优化算法经过参数和吸引子搜索策略的融合后,使得问题搜索空间内的粒子进入可行域内机会显著增加的缘故,同时,采用QPSO算法优化求解的结果误差达到了算法的精度要求,而其他2种算法获得是目标函数的近似解。另外,通过预估计每吨矿石的单位采运成本与3种算法的计算结果进行求差后发现,用非线性方法计算后相差0.2元/吨,用粒子群算法计算后相差0.38元/吨、用量子粒子群算法计算后相差0.45元/吨,从金属矿山企业长期资金投入的角度来看,这依然会给企业生产投入节约不少成本。 表5 优化后的矿石品位指标对比 从表5的结果可以得知,在金属矿山企业生产计划指标一定的情况下,对富含4种矿石元素的品位指标进行优化计算后,利用非线性规划方法和基本粒子群算法优化计算后的入选矿石品位几乎无法满足选厂指定的品位值,只有钨、铜金属品位指标达标;利用量子粒子群优化算法后,达到选矿厂入选的矿石品位指标明显要比计划期内的指标高出很多,而且矿石的开采率也比计划期内的指标高出1.0%左右,这可以充分说明QPSO算法在求解生产计划模型的优越性,特别是对于矿产资源的开采利用效果的显著变化,因为在QPSO算法中引入双层可行域搜索策略后,使得非可行域内的粒子有更多的机会向可行域内靠拢,增强了生产计划模型求解的可行性,从而能够获得更多的优化求解结果。 表4 金属矿山生产计划优化结果 (1)针对金属矿山企业生产计划的复杂编制问题,设计出符合企业实际生产需求的计划编制原则,并在模型构建的假设条件下,采用0-1整数规划方法,构建了金属矿山企业生产计模型,抽象地表达了金属矿山企业开采生产过程。 (2)针对基本量子粒子群算法求解金属矿山企业生产计划模型速度慢、结果精度低等问题,采用进化速度和聚集度因子对算法中的惯性权重系数进行了改进,同时,提出了双层可行域搜索的新型策略,提高了量子改进量子粒子群算法的搜索计算速度和求解精度。 (3)通过以某金属矿山企业的开采运输生产作业任务为案例,验证了矿山企业生产计划优化方法的可行性,并检验了模型求解软件的速度和算法的计算时间,其优化结果要比基本进化算法和模型求解软件的效果更好,为矿山企业生产投入成本与获利计算奠定基础。金属矿山企业生产计划优化方法是对智能优化算法的改进和拓展应用,今后将该算法与其他人工智能算法进行深度融合应用是本文进一步研究的方向。2.3 矿山企业生产计划的编制方法
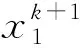
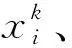
3 案例仿真实验与结果分析
3.1 工程案例与数据来源
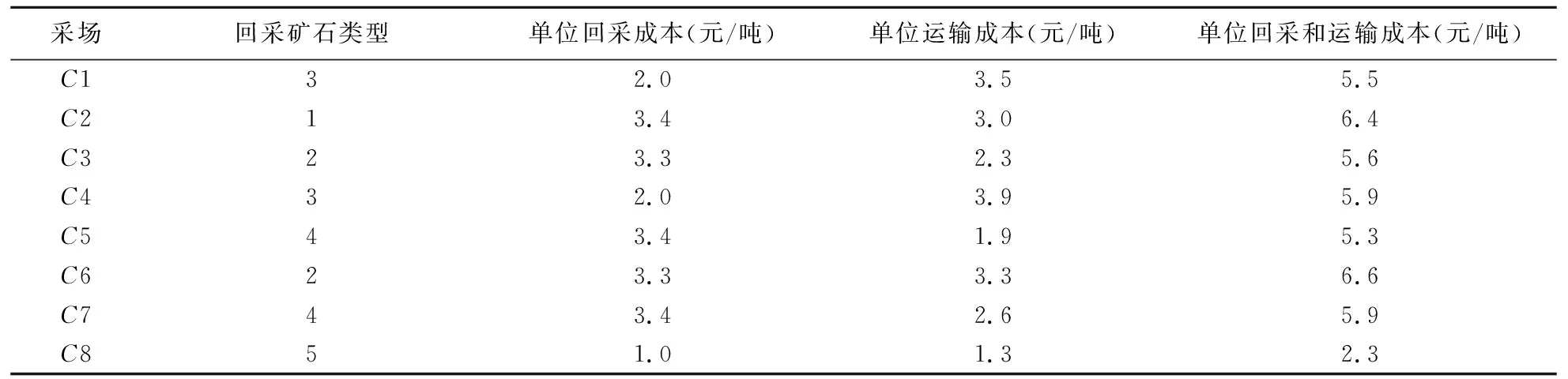
3.2 结果与对比分析
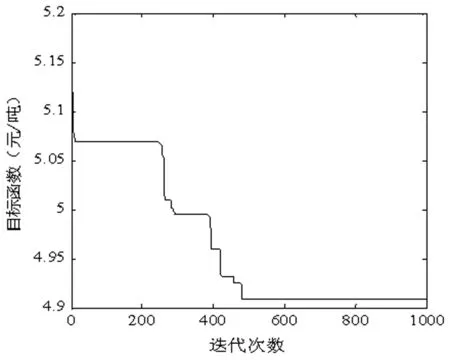
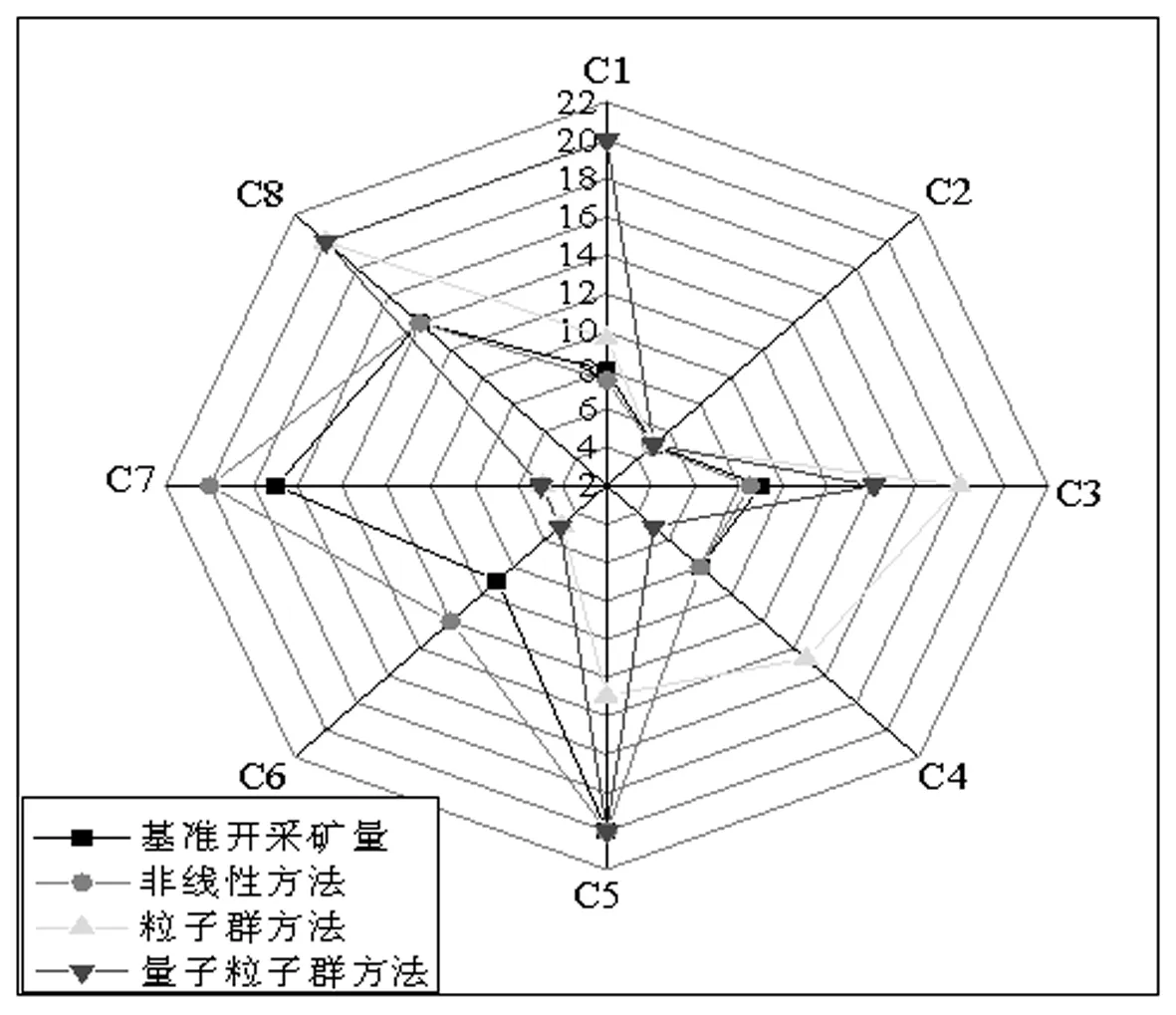

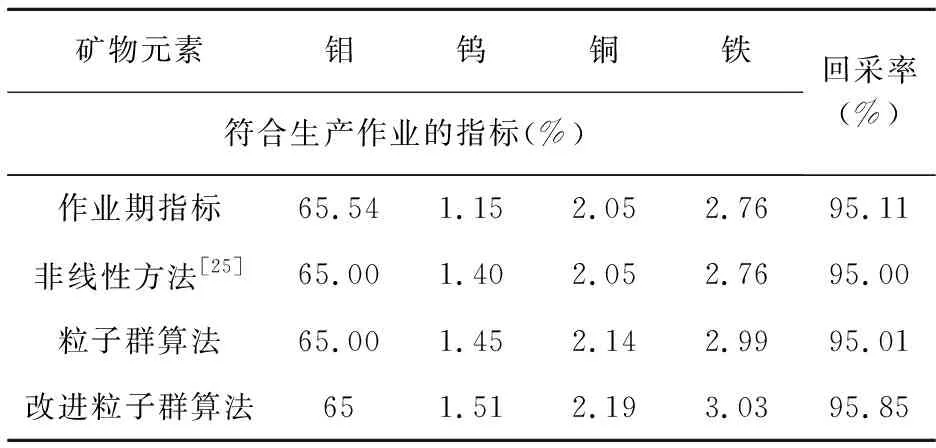
4 结论

