招标采购中的采购物品打包模型及其优化算法
黄学文,孙 榕,艾亚晴
(大连理工大学 管理与经济学部,辽宁 大连 116023)
0 引言
招标采购(Procurement Auction)也称逆向拍卖(Reverse Auction),是招标者(采购商)提出一组货物和服务(统称为物品)的采购要求,邀请指定或非指定的投标者(供应商)参与投标,按照一定程序和规则选择中标者的一种有效的市场交易行为[1],招标采购作为一种价格发现机制在国内外得到广泛应用[2]。
当采用采购招标来购买一组物品时,采购商需要在拍卖活动开始之前解决如下的问题:哪些物品需要打包成一个采购包?以及在保证充分市场竞争性的前提下,需要多少个采购包来完成全部物品的采购?其中,打包(bundling或lotting)是指采购商将多个物品捆绑成一个采购包[3],供多位供应商投标。另外,Schoenherr等[4]通过对30家美国公司的实证研究发现:在75.9%的招标采购活动中,要求或鼓励供应商对采购包中全部物品进行投标,被多数采购商尤其是大公司采购商所推崇。由此便产生一个问题——采购物品打包问题(bundling from buyer’s perspective),即:在要求候选供应商对采购包中的所有物品进行投标和确保候选供应商之间存在充分的市场竞争的前提下,如何确定一组互斥的采购包(任意两个不同的采购包中不能包含相同的物品)来满足采购商购买一系列物品的要求。目前,在中国的绝大数招标采购中,采购商要求供应商对采购包中的全部物品做出投标响应,同时,《中华人民共和国招标投标法》和《评标委员会和评标方法暂行规定》等法律文件规定每个采购包有不少于三家的候选供应商[2,5]。
作为逆向拍卖过程的一个关键参数和前置过程,采购物品打包对采购绩效有显著影响[2,3,6~11],如,降低采购过程的管理成本[12]、提高采购的规模经济[13,14]、增加采购商的议价能力[15,16]、缩短招标采购时间和减少采购约束条件[17]等。但不合理的采购物品打包策略会显著降低采购绩效[3,7,8],Estache等[8]通过实证研究表明:在公共基础设施建设项目中,不合理的采购物品打包策略严重限制了供应商之间的市场竞争性。
现实中存在两类不同的打包问题:采购物品打包和销售物品打包(bundling from seller’s perspective),销售物品打包是指卖方将两个或两个以上的物品捆绑销售。目前国内外研究主要集中于销售物品打包问题,关于该问题的研究,参见文献[18~21]。
关于采购物品打包问题的研究及成果较少,仅提出了几种概念性的采购物品打包策略,如,Jap[2]认为采购包应尽可能包含更多的物品,以降低其采购费用;但不能导致采购包的候选供应商数量减少,进而降低供应商之间的市场竞争性。相关学者[22~25]进一步提出为增加采购包中物品的数量,可将属于同一类别(commodity group)的物品打包在一起的策略。Beall等[6]提出两种打包策略:市场篮子打包(market basket lotting)策略和个体打包(individual lotting)策略,其中,前者适用于采购物品来源于相同或相似的物品类别且候选供应商能够供应全部或大部分采购物品的情况,经过80/20的帕累托(Pareto)分析后,最重要的物品打包在一起;个体打包策略适用于采购物品来源于不同的物品类别的情况,并将单一物品打包在一个采购包中。Linthorst等[26]基于采购人员的采访和总结,提出了同质打包(homogeneous bundling)策略和异质打包(heterogeneous bundling)策略,其中,将属于同一类别的物品打包在一起,称之为同质打包,反之则是异质打包。Hu等[27]定义市场竞争性(market competitiveness)和物品相似性(item similarity)两个变量,来度量两种物品打包在同一采购包的可能性,并提出了PBBS(Post-Bidding Bundle Strategy)采购物品打包策略;汪定伟等[28,29]在采购物品的价格互补性和投标一致性的基础上提出了基于量子算法的打包算法;唐振宇和廖腾芳等[30,31]针对图书馆期刊采购问题设计了基于双聚类算法的打包算法;孟碟和张智慧等[32,33]面向工程建设类项目提出了基于交易成本经济学的打包算法。此外,Schoenherr等[3,7]和Linthorst等[26],采用实证分析方法建立了一系列采购包属性用于评价采购包的价值和最佳采购物品打包程度,如物品定义难度(item specification difficulty)和采购包复杂性(overall bundle complexity)等。
文献综述表明:Jap所提出的采购物品打包理论已成为该问题的基本原则;但目前的采购物品打包策略多属于概念性方法,尚未形成通用性的采购物品打包优化模型和定量分析方法;同时,基于实证研究所提出的诸多采购包属性既难于度量又对采购绩效有相互依赖性的影响,从而难以通过这些采购包属性对采购物品打包问题进行定量分析。
本文将通过对采购包和采购打包方案等概念的定义,建立采购物品打包问题的0-1整数规划模型;同时针对该模型的NP-hard特点,首先将其转化为旅行商问题(Traveling Salesman Problem, TSP),并基于遗传算法(Generic Algorithm, GA)设计采购物品打包问题的求解算法;最后通过一系列的数据实验以验证算法的优化性能和计算效率。
1 问题描述
1.1 基本概念和定义
(1)物品-供应商矩阵
设采购物品集合为G={1,2,…,n},候选供应商集合为V={1,2,…,m},则物品-供应商矩阵为G×V=(eij)n×m,eij∈{0,1},物品i若可以由供应商j提供,则eij=1,否则eij=0。

物品-供应商矩阵可通过供应商管理系统以及RFQ(Request For Quote)、RFI(Request For Information)或RFP (Request For Proposal)等手段获得,物品-供应商矩阵定义了招标采购的基本信息。
(2)采购包
采购包是由一种或多种的采购物品构成,供不少于λ(λ∈Z+)个且尽可能更多的候选供应商投标,任意候选供应商应对采购包中的全部物品进行投标。采购包的候选供应商数量决定了该采购包的供应商之间的市场竞争性[34],最小市场竞争性由市场竞争控制参数λ决定。文献以及实际的招标采购中,一般建议λ=2[6],或λ=3[7]。
根据采购包的定义,任意采购包b可表示为一个矩阵Gb×Vb=(1)nb×mb,其中,Gb(Gb⊆G)表示该采购包中的物品集合,Vb(Vb⊆V,|Vb|≥λ)表示该采购包的候选供应商集合。
给定矩阵G×V和参数λ,存在满足采购包定义的一个潜在采购包集合Ω={b1,b2,…,bN}。N(N=|Ω|)由矩阵G×V和参数λ决定的,Ω可通过枚举法获得,但当G×V=(1)n×m且|V|≥λ时,有N=2n-1,即:枚举法计算潜在采购包集合Ω,会带来组合爆炸问题。
(3)采购打包方案
采购商为采购全部物品G,需要设计由若干采购包构成的某种采购打包方案,采购打包方案S定义为:S={b1,…,bSk},且满足如下三个条件:
1)bi∈Ω,1≤i≤Sk;
2)∀i≠j,有Gbi∩Gbj=ø;
3)∪bi∈SGbi=G。
其中,Sk为S中的采购包数量(|S|=Sk),条件2)表示S中任意两个不同的采购包在物品集合上互斥;条件3)表示采购打包方案S覆盖全部的采购物品。
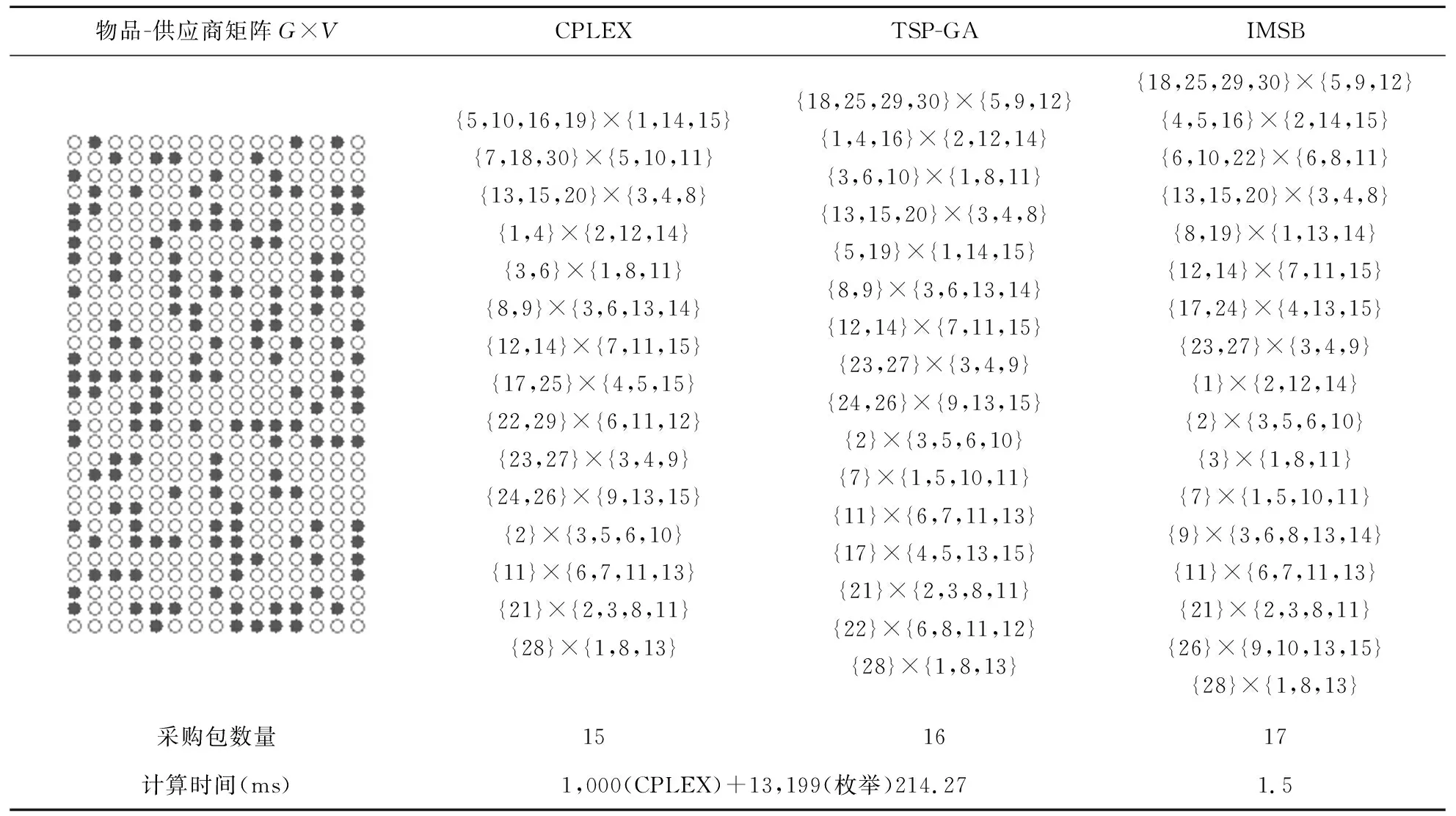
表1为五个物品和五个供应商的采购问题实例,若参数λ=3,采用枚举法可知共有11个潜在采购包;针对该问题,可设计多种采购打包方案,如S1={b1,b2,b3,b4,b5}、S2={b1,b3,b11}等。

表1 采购物品打包问题的示例
值得注意的是:b2={2}×{1,2,3,4}是仅包含物品2的唯一满足采购包定义的采购包,尽管{2}×{1,2,3}、{2}×{1,2,4}、{2}×{1,3,4}和{2}×{2,3,4}都有3个供应商,满足λ=3的要求,但不满足“尽可能最多的供应商”的要求,因此这些采购包是不合法的。事实上,仅包含物品2的采购包最多有4个供应商,即供应商1、2、3和4。
1.2 问题模型
关于采购物品打包问题,Grimm等[24]提出了贴合招标采购整体目标的两个子优化目标,即:最小化采购成本和将采购包分配给成本最低的供应商;但度量这两个目标依赖于供应商的投标数据(如价格、质量、交货等),而供应商的投标对象则是采购物品打包的结果——采购包,即:供应商的投标活动发生在采购物品打包活动之后,因此,上述优化目标无法在采购物品打包过程使用。
本文将最优采购物品打包方案定义为“在保证充分市场竞争性的前提下,包含最小采购包数量的采购打包方案即为最优采购打包方案”。由于采购包的定义已经保证了每一个采购包有不少于λ个的候选供应商,即每一个采购包都有充分的市场竞争性,因此,采购物品打包问题的优化目标为最小化采购打包方案中的采购包数量。
上述观点与Jap的采购物品打包理论是一致的:其一,采购包的定义确保了候选供应商之间有充分的市场竞争性;其二,最小化采购打包方案中的采购包数量,则意味着最大化采购打包方案中的采购包的平均物品数量(|G|/|S| )和平均采购费用C/|S| (设C为采购全部物品的期望费用),显然,这样的采购打包方案会增加候选供应商的投标积极性,并给采购商带来更强的议价能力[16,26];其三,由于包含更少的采购包,可以加速招标采购的执行过程,减少招标采购的管理成本。
因此,采购物品打包问题可定义为:给定物品-供应商矩阵G×V和市场竞争控制参数λ,寻找某种采购打包方案,且该方案包含最小数量的采购包。在给出问题的数学模型之前,先给出如下假设条件:
1)∀g∈G,有|V(g)|≥λ;
2)∀g∈G,其采购数量可由V(g)中任意一家候选供应商的供货能力所覆盖;
3)∀供应商v∈V,均是采购商的合格供应商(如产能、供货,商誉等);
4)∀供应商v∈V,在其能力范围内,不会放弃可能的投标机会。
基于以上假设,采购物品打包问题可表示为如下的0-1整数规划模型:
(3)
式中,xb是决策变量,用来判断最终的采购打包方案是否选中了采购包b(b∈Ω),xb=1表示采购包b被选中,否则xb=0;参数δgb∈{0,1},若物品g打包在采购包b中则δgb=1,否则δgb=0。式(1)表示采购物品打包问题的优化目标为最小化采购打包方案中的采购包数量,式(2)表示采购物品集合中的任意一种物品必须包含于采购打包方案中,且只能被打包到唯一采购包中。
从式(1)~(3)可以看出:上述模型延续了Jap等人所提出的概念化采购物品打包理论或策略,并将这些概念化的理论或策略转化成精确的0-1整数规划模型,为求解优化的的采购物品打包方案提供了一种数学分析方法。
如,对于表1中的问题,共有11个潜在的采购包,因此有11个决策变量向量x1,x2,…,x11,参数δgb可以由如下的矩阵δ=(δgb)5×11表示:

矩阵δ中第i行表示物品i,第j列表示第j个采购包,如δ37=1表示了在采购包b7中包含了物品3(见表1),则该问题的整数规划模型如下:
minz=x1+x2+…+x11
s.t.x1+x6=1
x2+x6+x7+x8+x9+x11=1
x3+x7=1
x4+x8+x10+x11=1
x5+x9+x10+x11=1
xi∈{0,1},∀i=1,2,…,11
1.3 问题复杂性分析
命题1采购物品打包问题是NP-hard问题。
证明该命题的证明是通过说明采购物品打包问题分别是集合分区问题(Set Partitioning Problem, SPP)和双聚类问题(Bi-clustering Problem)的实例。由于这个两个问题均是NP-hard问题[35,36],因此,采购物品打包问题是NP-hard问题。
(1)集合分区问题
集合分区问题的定义如下[37]:给定一个行集合M={1,…,m}和列集合N={1,…,n},如果第j列(其权重为cj,cj>0)包含行集合中的元素i∈M则aij=1,否则aij=0,集合分区问题的目的是寻找一个最小权重的集合M的分区(partition),其数学描述如下:


xj∈{0,1},∀j∈N
其中,决策变量为xj,当第j列选中到最后的分区中则xj=1,否则xj=0。
如果将潜在采购包集合Ω中的每个采购包b∈Ω中的物品集合Gb看成是集合分区问题中权重恒为1的一列,并将采购物品集合G看成是集合分区问题中的行集合,则采购物品打包问题是集合分区问题的一个实例。
(2)双聚类问题
双聚类问题定义如下[36]:给定一个矩阵A(I,J),其中,I={1,…,n}为行集合(或基因集合),J={1,…,m}为列集合(或条件集合),矩阵中的元素aij∈R表示第i行基因在第j列条件下的表达值。一个双聚类A(I0,J0)是矩阵A(I,J)的一个子矩阵,其中,I0⊆I且J0⊆J。双聚类问题的目的是寻找满足某种同质性标准的一组双聚类。
按照定义,任何一个采购包是矩阵G×V的一个子矩阵,且其元素均等于1,因此,一个采购包是矩阵G×V的一个常聚类(constant bi-cluster);同时,任何采购打包方案S={b1,…,bSk},按照定义,满足Gbi∩Gbj=ø(i≠j)和Ubi∈SGbi=G,即:采购打包方案S={b1,…,bSk}是矩阵G×V的行独占型双聚类。因此,采购物品打包问题可以看成是一个矩阵G×V的双聚类问题的实例。
由此,命题1得证。命题1说明:采购物品打包问题具有很高的计算复杂性,单纯依靠概念性的打包理论(如Jap的采购打包理论[1])或打包策略(如Beall等的打包策略[6])以及实际经验来指导采购物品打包是很难获得优化的采购打包方案,特别是对于中、大规模的招标采购问题。
命题2采购物品打包问题是一类比集合分区问题更为复杂的问题。
证明命题1证明了采购物品打包问题是集合分区问题的一个实例。
但是,采购物品打包问题和集合分区问题有着很大的差异,其差异体现在如下两个方面:
(1)集合分区问题的列集合是事先给定和已知的,但若将采购物品打包问题视为集合分区问题,其列集合,即潜在采购包集合Ω,不是事先给定的;
(2)枚举法是获得潜在采购包集合Ω的唯一方法,对于中、大规模招标采购问题,会导致组合爆炸问题。正如前文所述,当G×V=(1)n×m且|V|≥λ时,潜在采购包的数量高达2n-1。
由此,命题2得证。命题1意味着采购物品打包问题可用集合分区问题和双聚类问题的现有算法来求解。目前,集合分区问题和双聚类问题均有成熟的求解算法。对于集合分区问题,已有一些精确算法(如列生成算法、商用数学规划软件等)和启发式算法(如并行遗传算法)[38,39];对于双聚类问题[40],有MSB算法(Maximum Similarity Bi-cluster algorithm)、FLOC算法(Flexible Overlapped Bi-clustering)、SA-B算法(Simulated Annealing Bi-clustering)和CTWC算法 (Coupled Two-way Clustering)等算法。然而,由于采购物品打包问题属于NP-hard问题,因此,若将这些现成的算法直接用于求解一定规模的采购物品打包问题,只能得到近似最优解。另一方面,命题2说明:用于求解集合分区问题的现成算法或只适用于求解小规模的采购物品打包问题。与此同时,现成的双聚类算法不能保证“双聚类中的列数量不小于λ”的要求(采购包有不能小于λ个候选供应商),即原始的双聚类算法并不完全适用于采购物品打包问题,它需要一定的改造并满足双聚类中的列数量不小于λ的要求后才可以用于求解采购物品打包问题。
在求解采购物品打包问题时,将选用商用数学规划软件——CPLEX(Version 12.2)和一种双聚类算法——MSB算法,作为对比算法来比较本文所提算法的优化性能。
2 基于TSP和GA的优化算法
2.1 采购物品打包问题的TSP模型
旅行商问题(TSP)是研究历史最为悠久的经典组合优化问题并有更为广泛和成熟的求解算法,其定义如下[41]:设图Graph=(V,E),V是N个顶点的集合,E为边集,设C=(cij)是一个与E有关的非负距离矩阵。TSP的目标是寻找一个具有最短长度的巡回路径,且该巡回路径有且只有一次经过每一个顶点。
某种意义上讲,一个采购打包方案类似于采购物品集合G意义上的一个巡回路径,这是因为:任何一个物品只能打包在采购打包方案中唯一的采购包中,即任意一个采购打包方案有且只有一次地“访问”了每一个物品。
因此,若将采购物品集合G看成是TSP问题的顶点集合,采购物品集合G意义上的一个巡回路径长度看成是该路径所对应的采购打包方案中的采购包数量(后文给出相应的解码算法)。则采购物品打包问题可以看成是如下的一个TSP问题。
min|{xij=1│i,j∈G}|
(4)
其中,若有向边(i,j)包含在巡回路径中则xij=1,否则xij=0 ;集合{xij=1│i,j∈G}表示由n个xij=1所构成的巡回路径,|{xij=1│i,j∈G}|表示该路径的距离,即:该路径所对应的采购打包方案中的采购包数量。式(4)表示问题的优化目标,即最小化巡回路径所对应的采购打包方案中的采购包数量,式(5)、(6)和(7)表示每一顶点(物品)在巡回路径中只出现一次。
巡回路径R={xij=1│i,j∈G}为集合G的一个全排列,即R={g1,g2,…,…,gn},巡回路径采用如下的BUNDLING算法解码为采购打包方案,该算法中用到如下的数学符号:
(1)运算符⊗:对于矩阵G×V的任意两个行向量:i=(ei1,ei2,…,eim)和j=(ej1,ej2,…,ejm),有:i⊗j=(e1,…,ek,…,em),ek=eik·ejk,k=1,2,…,m;
(2)aBundle表示一个采购包,它由两个元素构成:Items和Suppliers,其中,Items表示采购包中的物品集合;Suppliers表示候选供应商集合;若aBundle=Ø,则有aBundle.Items=Ø和aBundle.Suppliers=Ø;
(3)BunSolution表示采购打包方案。
算法BUNDLING的具体步骤如下:
Step1输入巡回路径R={g1,g2,…,gn}和参数λ;
Step2初始化:BunSolution=Ø;aBundle=Ø,向量R*=(1,…,1)∈R|V|,循环变量j=1;
Step3Repeat
Step3.1R=R*⊗gj,其中gj为路径R={g1,g2,…,gn}中第j个物品gj所对应的行向量;
Step3.2如果Sum(R)≥λ且j Step3.3如果Sum(R)<λ或j=n,则:R*中分量为1所对应的供应商集合记为tempSup,aBundle.Suppliers+=tempSup,BunSolution+={aBundle};重置aBundle=Ø和R*=(1,…,1)∈R|V|; Step3.4循环变量j=j+1; Step4Untilj=n; Step5输出采购打包方案,即BunSolution。 如对表1中的问题,若巡回路径为R=(2,4,5,3,1)(即:x24=1,x45=1,x53=1,x31=1,x12=1)和λ=3,则该路径将解码为采购打包方案{b11,b3,b1},即{{2,4,5}×{1,3,4},{3}×{1,3,4},{1}×{2,3,4} }。这是因为:R*⊗i2⊗i4⊗i5=i2⊗i4⊗i5=(1,0,1,1,0)、Sum(i2⊗i4⊗i5)=λ、i2⊗i4⊗i5⊗i3=(1,0,1,0,0)且Sum(i2⊗i4⊗i5⊗i3)=2≤λ,故第一个采购包将包含3个物品,即{2,4,5};并有候选三个潜在供应商,即{1,3,4}(i2⊗i4⊗i5的第1、第3和第4个分量为1);同时,第二个采购包从该路径的第4个元素开始,又因为i3⊗i1=(0,1,1,0,0)和|i3⊗i1|<λ,故:第二个采购包为b3={3}×{1,3,4},第三个采购包为b1={1}×{2,3,4}。 从式(4)~(9)来看,正是由于BUNDLING算法的提出,从而使得采购物品集合G意义上的一个巡回路径可以解释成一个采购打包方案,进而使得采购物品打包问题可以表达为TSP问题。 旅行商问题有着广泛而且成熟的求解算法,其中,元启发式算法(metaheuristic algorithms)是一类重要的求解算法[41]。本文选用遗传算法(GA)来求解采购物品打包问题的TSP模型,该算法采用GA的标准流程,此处不再赘述,以下介绍其主要组成部分,如:种群初始化、染色体编码和解码、适应度评价、交叉与变异算子和个体选择机制等。 2.2.1 染色体编码和解码 染色体编码直接采用采购物品集合G的全排列,如前文所述,采购物品集合G的任意一个全排列,表示了集合G意义上的一个巡回路径。以表1中的问题为例,其染色体编码如图1所示: 25134 染色体的解码直接采用BUNDLING算法,该算法将染色体解码成合法的采购打包方案。 2.2.2 种群初始化、适应度评价和个体选择机制 按照染色体编码策略,随机构造遗传算法的初始种群。 由于采购物品打包问题的优化目标为最小化采购包数量,故染色体i的适应度定义为: Fit(i)=n+1-|BunSolution(i)| (10) 其中,BunSolution(i)表示染色体i所对应的采购打包方案,|BunSolution(i)|表示该采购打包方案中的采购包数量,由适应度的定义可知:Fit(i)≥1,这是因为:最恶劣的采购打包方案是一个采购包有且只包含一个物品,要采购全部物品,则最多有n个采购包。 选用带有精英保留策略的轮盘赌选择机制,即染色体i的生存概率定义为: (11) 其中,Popsize为遗传算法的种群数量。 2.2.3 交叉和变异算子 为避免产生不合法的染色体,选用POX交叉算子(Precedence Preserving Order-based Crossover)[42]。其过程如下:随机选择两条染色体P1和P2,初始化两条空的子代染色体O1和O2,将采购物品集合G随机划分为两个非空子集G1和G2;将P1中属于集合G1中的元素所对应的基因复制到O1的相同位置上,再将P2中属于集合G2中的元素所对应的基因从左到右依次填充到O1的空位上;互换P1和P2的角色得到O2。O1和O2为P1和P2的交叉结果。 以表1中的问题为例,图2为POX交叉算子的运算实例。 图2 交叉算子实例 变异算子则采用简单的两点倒位变异算子,即随机选择两点并且两点之间元素倒序排列。 采用C-Sharp(C#)语言实现了上述采购物品打包算法(以下简称TSP-GA算法),并进行了若干数据实验,测试环境为:Windows 7操作系统,CPU i7 2.9G,内存4G。 选择了两种测试算法来对比分析TSP-GA算法的性能,即:(1)将采购物品打包问题视为集合分区问题的实例,采用商业线性规划工具软件CPLEX(Version 12.2)来求解;(2)将采购物品打包问题视为双聚类问题的实例,采用MSB算法来求解(关于MSB双聚类算法,参见文献[43])。 如前文所述,将采购物品打包问题视为集合分区问题的实例,需要预先采用枚举法生成全部的潜在采购包,而这会产生组合爆炸问题,因此,集合分区问题的算法只能解决小规模的采购物品打包问题。 MSB算法是一个优秀的双聚类算法,能够发现包含更多行和列的具有最大相似性的双聚类;但正如前文所述,MSB算法所发现的双聚类并不能保证“列数量不小于λ”的要求(采购包有不能小于λ个候选供应商)。为此,本文对MSB算法做适当改进,以确保改进后的MSB算法(Improved MSB approach,IMSB)所发现的双聚类的列数量不小于λ的要求。 IMSB算法的具体步骤如下: Step1输入矩阵G×V和参数λ; Step2初始化如下变量:BunSolution=Ø,aBundle=Ø; Step3Repeat Step3.1置参考基因R*=(1,…,1)∈R|V|; Step3.2计算矩阵G×V当前的在参考基因R*下的最大相似性双聚类(Maximum Similarity Bi-cluster),记为A(I*,J*); Step3.3如果|I*|≥2且|J*|≥λ,则:aBundle.Items+=I*、aBundle.Suppliers+=J*、BunSolution+=aBundle;G=G-I*,aBundle=Ø; Step4Until|I*|=1或|J*|<λ; Step5若|G|≠0,则对于任意物品g∈G,做aBundle=Ø,aBundle.Items+={g},aBundle.Suppliers+=V(g)和BunSolution+={aBundle}; Step6输出采购打包方案,即BunSolution。 其中,参考基因设为R*=(1,…,1)∈R|V|,以确保寻找到的双聚类中的元素永远为1,从而满足采购包的定义;Step 3.3将每一个列数量不小于λ的双聚类输出成一个采购包;Step 5则将G中双聚类后剩余的每一个物品均打包成单一的采购包。 现有文献中尚未有采购物品打包问题的标准算例。为此,采用随机的方式建立了七个不同规模的采购物品打包问题,即:30/15/8、50/50/14、80/80/15、100/100/15、500/100/25、1000/200/35和1500/250/40。问题均表示成|G|/|V|/r的形式,其中,|G|表示采购物品的数量,|V|表示供应商的数量,r(λ≤r≤|V|)是一个非负整数。对于每个采购物品打包问题,矢量g(即任意采购物品)在满足条件λ≤Sum(g)≤r的前提下随机生成。 七个不同规模的采购物品打包问题,市场竞争控制参数均设为λ=3。对于其中的30/15/8问题,采用枚举法求其全部的潜在采购包。 若干实验后,TSP-GA和IMSB算法中参数设置如下:IMSB算法的α=0.4,β=0.5(α,β为MSB算法的内置参数);TSP-GA算法的交叉概率为PC=0.4,变异概率为PM=0.1;对于第1个测试问题:Popsize=50,IteNo=50(遗传算法的迭代次数);对于第2、3个测试问题:Popsize=50,IteNo=100;对于第4个测试问题:Popsize=80,IteNo=100;对于第5、6个测试问题:Popsize=100,IteNo=100;对于第7个测试问题:Popsize=100,IteNo=120。 表1给出了小规模问题30/15/8的优化结果,其物品-供应商矩阵G×V采用点阵图表示(实心点表示数1,空心点表示数0),通过枚举法求得潜在的采购包共174个,枚举耗时13,199毫秒(ms)。其中,CPLEX求得该问题的最优解——15个采购包,CPLEX纯粹用于计算时间为1,000ms,加上CPLEX所必须的枚举潜在的采购包的时间(13,199ms),则CPLEX所需要的全部时间远高于TSP-GA和IMSB算法的计算时间;TSP-GA算法的优化性能非常接近最优解,而IMSB算法优化性能稍差,但IMSB算法具有最快的计算速度。 造成这一现象的原因是:IMSB算法属于贪心搜索算法,故而收敛速度很快,但易陷入局部最优[50],即容量更大的双聚类很难被发现;TSP-GA算法属于全局搜索进化算法,有效地克服了贪心算法的缺点。同时,TSP-GA算法和IMSB算法均无需事先枚举潜在的采购包,故这两种算法相对于CPLEX具有明显的计算速度优势。 表2 30/15/8问题的优化结果 七个不同规模问题的优化结果如表3所示,结果表明:TSP-GA和IMSB算法均能较好地实现采购物品打包,其中,TSP-GA算法具有更好的优化性能,能获得包含更少采购包的采购打包方案;IMSB算法的计算时间小于TSP-GA算法的计算时间的1%,具有明显的计算速度优势;同时,随着问题规模的增大,两种算法所求得的采购打包方案的采购包数量上的差值呈增长趋势。 表3 不同规模问题的优化结果 TSP-GA算法的计算时间明显高于IMSB算法,且计算时间随着问题规模的增加而增加。但相对于问题的规模而言,其运行速度尚在可以接受的时间范围内,如:对于七个问题中的最大规模的问题1500/250/40,计算时间仅为1476秒。这表明TSP-GA算法可以应用于实际的大规模招标采购问题。如,国内的药品集中招标采购属于典型的大规模招标采购问题(为了规范医疗机构药品购销工作和减轻社会医药费用负担,我国自2000年起开始实施药品集中招标采购)。文献[27]描述了发生在2010年的第7界黑龙江省药品集中采购招标的情况,在本次招标采购中涉及到1147种不同药品。 采购商视角下的采购物品打包问题对招标采购的绩效有显著影响,本文从采购商的角度出发,通过对采购包、采购打包方案以及最优采购打包方案等概念的定义,首次建立了采购物品打包问题的通用型数学模型,该模型延续了Jap等人所提出的概念化的采购物品打包理论或策略;同时,指出该问题是集合分区问题和双聚类问题的实例,证明了采购物品打包问题属于NP-hard问题;随后,将采购物品打包问题转化成一类特殊的旅行商问题(TSP),并基于遗传算法设计了该问题的求解算法。实验结果表明:本文所设计的优化算法具有很好的优化性能和很高的计算效率。2.2 基于GA的优化算法


3 数据实验
3.1 测试算法
3.2 测试问题
3.3 小规模问题的优化结果分析
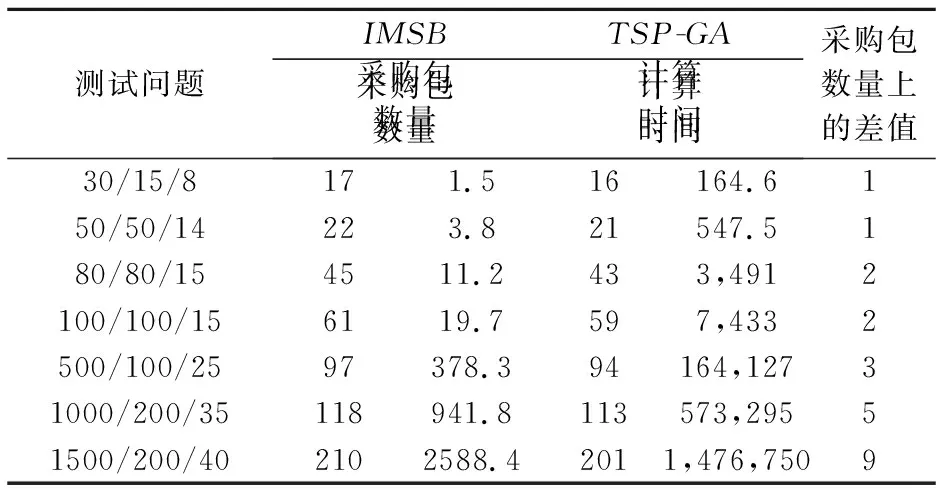
3.4 不同规模问题的优化结果分析
4 结论

