从实验熔合激发函数抽取势垒高度

崔丹腾，温培威，林承键,*，贾会明，王 宁，杨 磊，马南茹，王东玺，杨 峰，徐新星，孙立杰，钟福鹏，钟善豪

(1.广西师范大学 物理科学与技术学院，广西 桂林 541004；2.中国原子能科学研究院 核物理研究所，北京 102413)

重离子一般指较α粒子重的原子核，必须满足两个粒子之间有一定的相对运动能量才能发生核反应。重离子相互作用主要由排斥的库仑势VC和吸引的核势VN组成，两种不同性质的相互作用在一定距离处形成1个势垒，即库仑势垒，其高度VB在反应中扮演着重要角色。如对于熔合反应，即弹核克服库仑势垒被势阱俘获并形成复合核的过程，当反应能量E>VB时，弹核越过势垒被俘获，称为垒上熔合，这是经典的俘获过程；当E≤VB时，弹核穿过库仑势垒被俘获，称为垒下熔合，这是量子隧穿过程[1]。由此可见，库仑势垒的高度VB扮演了1个经典机制和量子机制转换点的角色。近垒反应通常是指反应能量相对于库仑势垒高度而言的。

熔合反应对于理解核力、超重核合成以及天体核合成等具有重要的意义，相关研究引起了关注。势垒高度是描述熔合反应的基本参数，目前已有较多理论模型来描述[2-5]，但给出的结果差别较大。由于势垒高度不能直接测量，需结合理论模型才能给出，因此存在一定的模型相关性[6-7]。

鉴于库仑势垒高度的重要性，本工作将采用一种新方法从实验数据提取库仑势垒高度，以降低所提取的参数对理论模型的依赖。考虑到目前很多体系已有高精度熔合激发函数的测量值，因此该方法主要思路是拟合实验熔合激发函数，将得到的截面与能量乘积对能量进行一阶微分得到穿透系数T，然后通过T确定势垒高度。还对所提取的势垒高度与不同理论模型预言的势垒高度进行系统分析比较，如Bass势[2]、亲近势[3]、CW76势[4]、BW91势[5]等，并对势垒高度随同位旋自由度的变化进行研究。

1 物理模型和拟合方法

采用实验熔合截面与能量的乘积相对于能量的一阶微分作为T，并将该T最大值一半的位置定义为VB，由如下条件得出：

(1)

其中：E为质心系反应能量；σfus为实验熔合截面。该公式只涉及实验熔合截面和反应能量，因此所定义的VB不依赖于理论模型。任何满足该定义的理论模型在实验误差范围内均能拟合出相同的结果。在实际操作中，将采用不同理论模型来拟合一些具有代表性的实验熔合激发函数，根据上述定义得到VB。

1.1 耦合道模型

重离子熔合反应是一个复杂的多维量子隧穿过程，涉及到众多自由度之间的耦合，如两核相对运动自由度与核内部集体运动自由度之间的耦合。获得多维量子隧穿概率的一个标准方法是求解耦合道薛定谔方程。目前已发展了多个耦合道模型，如完全耦合道的CCFULL模型等[8]。CCFULL模型因能处理径向运动和集体运动之间的全阶耦合，并能精确数值求解耦合道方程，所以得到广泛应用。耦合道方程通常表示为：

(2)

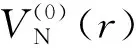
ψn(r)=

(3)

(4)

在CCFULL模型拟合实验熔合激发函数时，采用常用的Woods-Saxon势，即：

(5)

式中：V0为势强度；R为相互作用半径；a为表面弥散宽度。在考虑不同耦合的情况下，通过拟合这3个参数以符合实验熔合截面，进而根据式(1)提取VB。

1.2 Wong公式

在一维WKB势垒穿透公式的基础上，采用势垒分布抛物线近似、势垒位置以及曲率与角动量无关近似，并假设角动量连续变化，可得到一维势垒穿透Wong公式[9]。该公式形式简单，不依赖于具体的相互作用势，能较好描述无耦合时势垒能区的熔合截面，被广泛应用。依据Wong公式，熔合截面可表示为：

(6)

(7)

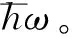
1.3 拟合方法及实验数据

拟合是通过寻找最小的每点χ2实现，每点χ2定义为：

(8)

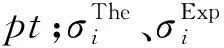
本工作共采用12组实验熔合反应体系：16O+112,116Sn[10]，32S+90,94,96Zr[11-12]，36S+90,96Zr[13]，32S+112,116,120Sn，40Ca+40Ca[14]和48Ca+48Ca[15]。这些实验体系是比较常见的体系，实验数据精度高、测量结果可靠，被关注较多，且包含不同的同位素，可研究势垒高度的同位旋相关性。

2 拟合结果与讨论

2.1 拟合截面和势垒高度提取

本工作采用CCFULL模型和Wong公式两种方法拟合实验熔合激发函数。在CCFULL模型的拟合中，需考虑合适的集体振动与径向运动的耦合，选取的耦合条件列于表1、2。表1列出了CCFULL模型计算中考虑的集体振动条件，包括激发态的自旋和宇称λπ、激发能Eλ、形变参数βλ和声子数NPh。另外，对于一些反应体系，如32S+90,94,96Zr等存在着明显的正Q值中子对转移引起的垒下熔合截面增强现象[11-12]。因此在采用CCFULL模型拟合计算中，也考虑了正Q值中子对转移的贡献。表2列出了CCFULL模型计算中考虑的集体振动耦合径向系数rcoup和Q。在以上耦合条件下，调节Woods-Saxon相互作用势的V0、R和a符合实验熔合激发函数后，通过式(1)可抽取实验势垒高度。

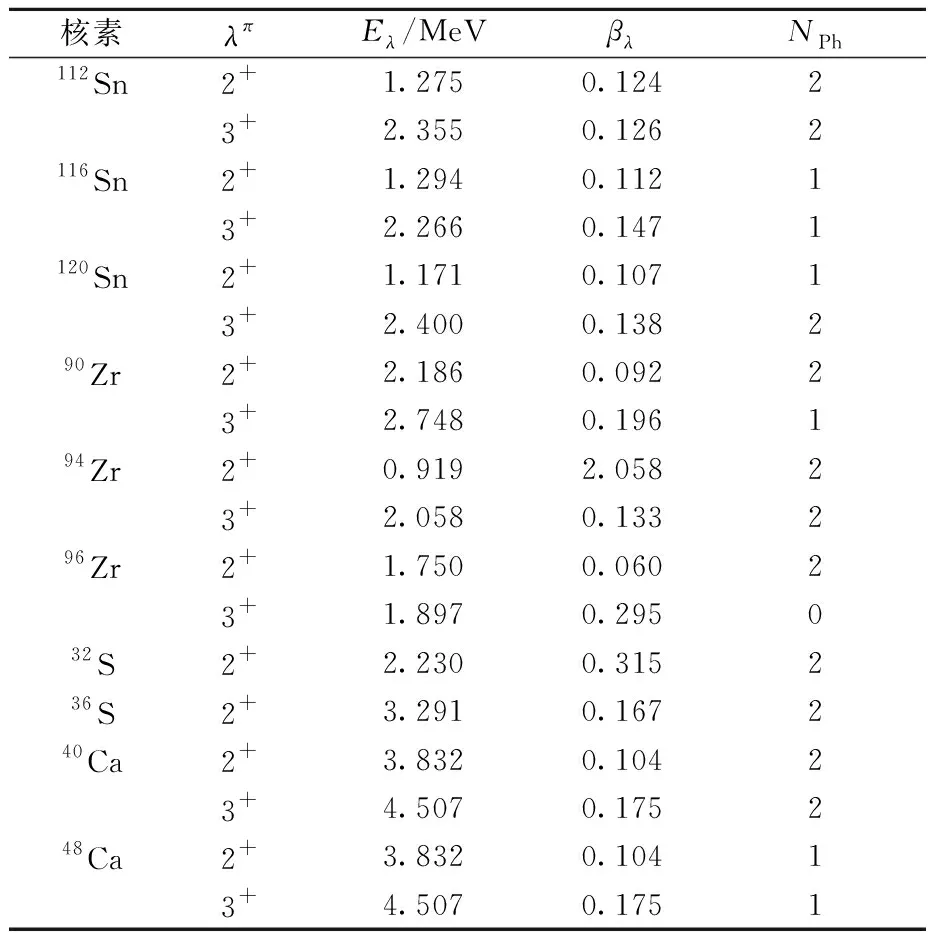
表1 CCFULL模型计算中考虑的原子核集体振动的参数Table 1 Adopted collective vibration parameters in CCFULL model calculation

表2 CCFULL模型计算中考虑的Q和rcoupTable 2 Adopted Q and rcoup in CCFULL model calculation

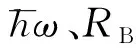
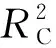
可看到，图2中垒上能区实验值的涨落和误差较大，理论值与实验值存在一定的偏差。需说明的是，垒上能区实验值涨落和误差大是方法本身固有的问题。从实验熔合激发函数抽取T是采用数值一阶微商的方法(式(1))，由于垒上能区熔合截面大，在相同能量步长dE下，d(Eσ)较垒下能区大很多，且截面测量的绝对误差也会传递到抽取的穿透系数中，导致垒上能区实验T的涨落和误差均很大。这与从实验熔合激发函数抽取的势垒分布在垒上的涨落和误差大的原因一致[16]。然而，拟合实验熔合激发函数抽取VB时，一方面，垒下截面对VB极其敏感，呈数量级的变化；另一方面，截面拟合后微商得到的理论T在垒上较高能区呈饱和，即相应于穿透概率P=1的情况，由此确定P=0.5处的VB。图2中垒上实验T的涨落和误差对所抽取的VB影响不大。

图1 不同反应体系的熔合截面随质心入射能量的变化Fig.1 Fusion cross sections for different reaction systems with respect to incident center-of-mass energy

2.2 不同模型预测势垒对比

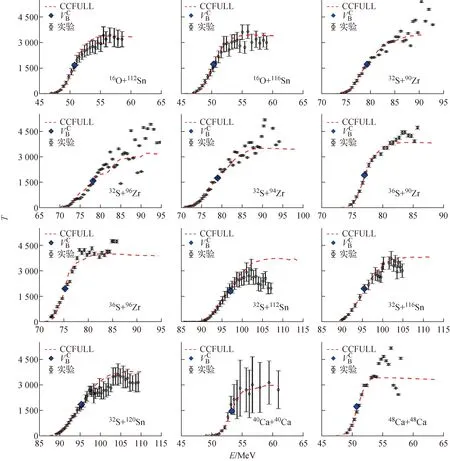
图2 穿透系数随能量的变化Fig.2 Tunneling coefficient with respect to energy

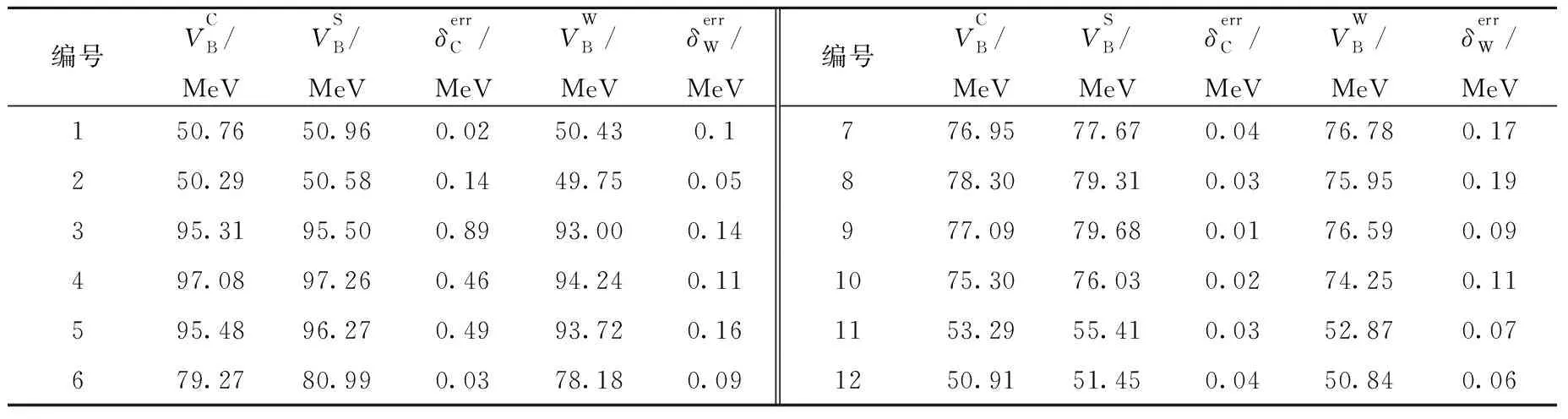
表3 由CCFULL模型和Wong公式抽取的库仑势垒高度Table 3 Extracted Coulomb barrier heights by CCFULL model and Wong formula

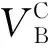
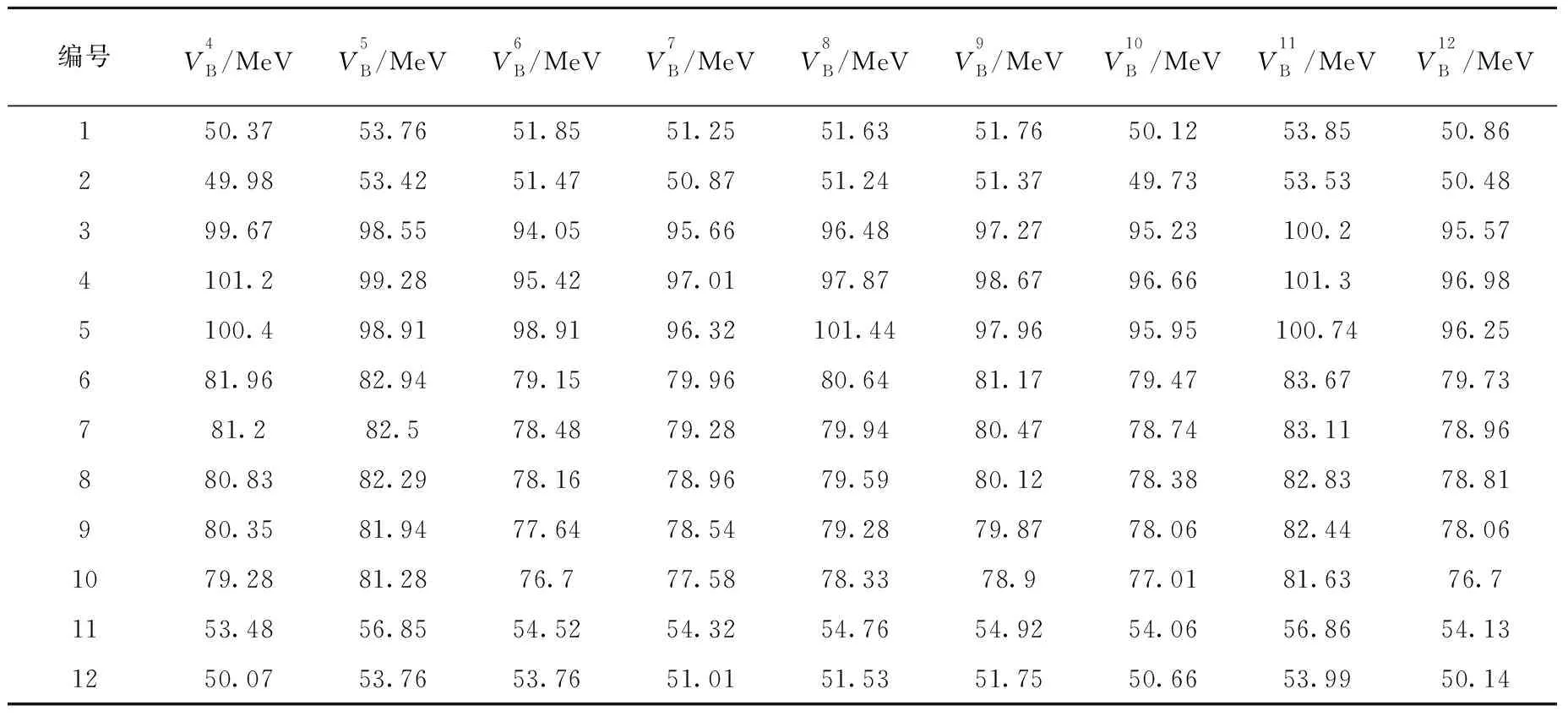
表4 不同理论相互作用势模型预测的势垒高度Table 4 Coulomb barrier heights predicted by different theoretical potential models

高的原因一致。另外，Bass80和WKJ公式的预测结果与本工作中由CCFULL模型从实验值抽取的势垒高度吻合最好。

图3 不同理论模型的库仑势垒高度与CCFULL模型拟合得到的势垒高度的比值Fig.3 Ratio of Coulomb barrier heights predicted by different theoretical models and CCFULL model

2.3 势垒同位旋相关性研究

本工作选择的12组实验熔合反应体系具有一定的同位旋相关性，可研究势垒高度随靶核同位旋不对称度η=(N-Z)/A的变化。以32S+ASn和32S+AZr体系为例，结果示于图4。可看出，随着同位旋不对称度的增加，势垒高度逐渐减小，这是中子数逐渐增多的效应。另外，CCFULL模型从实验值抽取的结果与Bass80和WKJ公式一致，这与从图3得到的结论相同，说明这两个理论模型均能较好地预测实验结果，可为其他体系势垒高度的预测提供参考依据。

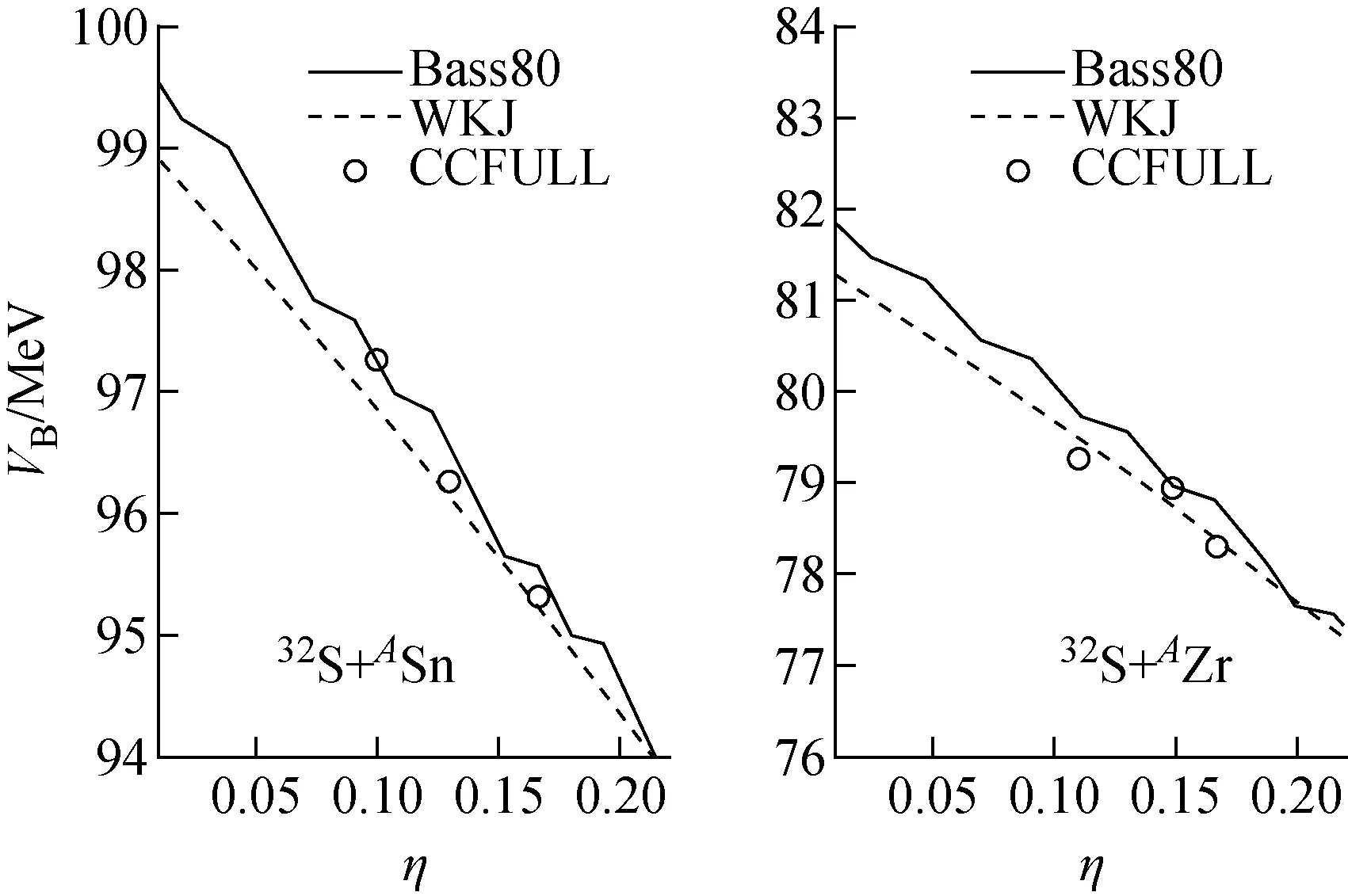
图4 由Bass80模型、WKJ公式和CCFULL模型得到的库仑势垒高度随32S+ASn和32S+AZr体系的同位旋不对称度的变化Fig.4 Coulomb barrier height with respect to isospin asymmetry for 32S+ASn and 32S+AZr by Bass80 model, WKJ formula and CCFULL model

3 小结

本文运用CCFULL耦合道模型和Wong公式，通过调节相应参数，拟合实验熔合激发函数以抽取势垒高度。根据熔合截面与能量乘积的一阶微分得到穿透系数，其最大值一半的位置即为势垒高度。该方法不依赖于理论模型，能抽取出较稳定的势垒高度。本研究选取了12组熔合反应体系，包括16O+112,116Sn、32S+90,94,96Zr、36S+90,96Zr、32S+112,116,120Sn、40Ca+40Ca、48Ca+48Ca。这些实验体系较常见，实验数据精度高、测量结果可靠，被关注较多，具有一定的代表性。通过调节相应参数，理论计算均能符合实验熔合反应数据。通过对比从实验值抽取出的库仑势垒高度和不同理论模型计算的结果，发现各理论模型计算的结果与从实验穿透系数中抽取的势垒高度的结果相差不大，但大部分偏高。通过系统的分析与比较后发现，Bass80模型和WKJ公式的结果与本工作结果吻合最好，且从势垒高度随同位旋不对称度的变化中也可印证该结论。在以后推测其他熔合反应的势垒高度，尤其是合成超重核的熔合反应势垒高度时，可优先考虑Bass80和WKJ公式，这将为探索合成未知超重核素的某些关键问题提供重要理论参考。