中国省际能源利用效率再测度＊

■ 李彦华 焦德坤 刘婧 武勇杰

中北大学经济与管理学院 太原 030051

0 引言

2015年，全球大约200个国家签订了《巴黎协定》，目标致力于将全球的温升控制在2 度。为了达到这个目标，一些学者或机构提出了碳预算的概念（即向大气里排放温室气体的最大限额），经测算，大约是3万亿吨，至今已用大约是75%，即2 万亿吨，还剩下大约7 千亿吨的温室气体排放空间。而每年全球排放的温室气体大约在400 亿吨，意味着到了2035年，全球的碳预算可能将消耗殆尽，即2035年以后，全球温室气体排放必须保持零排放，这对全球各国能源工业带来的挑战是巨大的。当今，我国作为世界上最大的能源消费国，据《BP世界能源展望2019年版》预计，到2040年，我国仍是全球最大的能源消费国，我国的碳排放则将在2020年达到顶峰。同时，煤炭在我国的能源消费比重中居高不下，对我国的环境造成了沉重的压力。所以，提高能源利用效率成为我国发展经济和节能减排合理并行的一个至关重要的因素。山西为煤炭资源大省，打造全国能源革命排头兵的政策对山西能源产业的发展具有十分重要的影响，考察政策落实情况对于进一步发展是必要的，山西省哲学社会科学规划办公室因此设立了《山西打造全国能源革命排头兵行动方案》对山西能源产业发展的影响研究课题，本文是该课题的部分成果，测度山西省能源利用效率并将其与全国其他省份进行比较，精准定位其能源利用效率发展现状及限制性因素，对于山西省能源产业的进一步发展具有十分重要的借鉴意义。

目前，能源利用效率测算相关文献主要涉及不同的区域、行业以及方法的改进和比较。其中，岳立[1-2]利用数据包络分析方法（Data Envelopment Analysis，DEA）的方向性距离函数（Directional Distance Function，DDF）和包含非期望产出的全要素生产率增长指数（Global Malmquist Luenberger，GML）测算了“一带一路”沿线50个国家的能源利用效率，并基于传统DEA 模型和Malmquist 生产率指数对中国和中亚5 国的能源利用效率进行了测算；孙伟[3]、关伟[4]分别基于松弛方向性距离函数（Slacks-based Measure，SBM）和超效率DEA模型对黄河流域62 个地级市的能源生态效率和9 省区的综合能源效率值进行了测算；刘海英[5]、厉桦楠[6]、孟洁[7]、于洋[8]和杜佳敏[9]等学者分别对我国省际能源利用效率进行了测算。关于行业能源效率的测算，肖智[10]、雷辉[11]对中国工业行业的能源利用效率进行了测算；宾厚[12]、张雪梅[13]、江兵[14]分别针对中国包装产业、兰州市节能环保产业、合肥市物流业的能源利用效率进行了测算；何伟怡[15]、陈亚[16]分别基于Bootstrap-DEA 模型和传统DEA模型对中国区域装备制造业的能源全要素生产率进行了测算。关于能源效率测算方法的应用及改进，主要是基于非期望产出涉及的两个问题：该指标替代变量的选取和处理方式。其中，研究中更多的是将二氧化碳、二氧化硫和“三废”作为非期望产出指标的替代变量。最初阶段，对于非期望产出的处理方法主要是将非期望产出变量取倒数，或者将非期望产出作为其投入变量[17,18]，这两种方法与实际情况不符，测算结果会有所偏差；发展阶段，学者通过坐标变换改变非期望产出变量的变化方向对能源利用效率进行研究[19,20]，使用该方法使产出为负的决策单元（Decision Making Unit，DMU）为有效状态，需要对此类DMU 再次进行测算；还有学者是通过方向距离函数来实现同时减少非期望产出和增加期望产出[21]，此方法弥补了前3 种方法的缺点，但与前3 种方法同属于径向的效率测度方法，会高估DMU 的效率值，结果区分度较低；目前应用最广泛且认可度较高的的方法是包含非期望产出的SBM-U 模型，该模型基于松弛变量对效率值的影响，使效率值有更好的结果区分度[22]。另外，基于方法的改进致使能源利用效率测算结果不一，从而对不同方法及指数测算的能源利用效率结果进行比较也成为当前研究的热点，彭树远[23]分别基于SBM模型、包含非期望产出的SBM-U 模型和非期望混合距离SBM 模型对中国全要素能源利用效率进行了测算，并将3 种模型测算的结果进行了比较；吴江[24]分别基于非期望产出不可分离的松弛方向性距离函数模型以及GML指数对中国全要素能源利用效率进行了测算。

综合上述分析，考察包含非期望产出的能源利用效率及其影响因素成为当前的研究热点，基于此，本文借鉴Aparicio[25]等人提出的至强有效前沿最近距离模型（minimum distance to strong efficient frontier，MinDS），该模型是基于SBM-DEA 模型改进而来的，结合Malmquist 生产率指数分别构建基于MinDS-DEA 模型和SBM-DEA 模型的全要素生产率指数模型：MinDS-M和SBM-M 模型，然后对中国省际能源利用效率进行评价，对现有研究内容和方法进行补充。文章具体从以下几个方面展开研究：（1）将基于MinDS-M 指数模型、SBM-M 指数模型以及包含非期望产出的MinDS-U-M指数模型和SBM-U-M 指数模型测算的结果进行比较分析，考察碳排放对我国能源全要素生产率的影响；（2）考察我国能源全要素生产率的时间序列特征和区域异质性；（3）考察我国能源全要素生产率的增长模式。

1 研究方法

1.1 MinDS-U-DEA模型

MinDS-DEA 模型是Aparicio 等人在SBM-DEA 模型的基础上进行了改进。投入或产出松弛变量最大化是实现SBM-DEA 模型优化的先决条件，但是这样可能会高估了无效决策单元的可改进空间。基于此，Aparicio 等人提出了MinDS-DEA 模型，该模型使被评估的DMU 到强有效前沿面的距离最小，弥补SBM-DEA 模型的缺点，后来学着扩展了SBM-DEA 和MinDS-DEA 模型，将非期望产出考虑到了模型当中，被称为SBM-UDEA和MinDS-U-DEA模型。

（1）经SBM-U-DEA 模型判定有效的决策单元的集合为Ecrs，SBM-U-DEA模型线性规划如下:

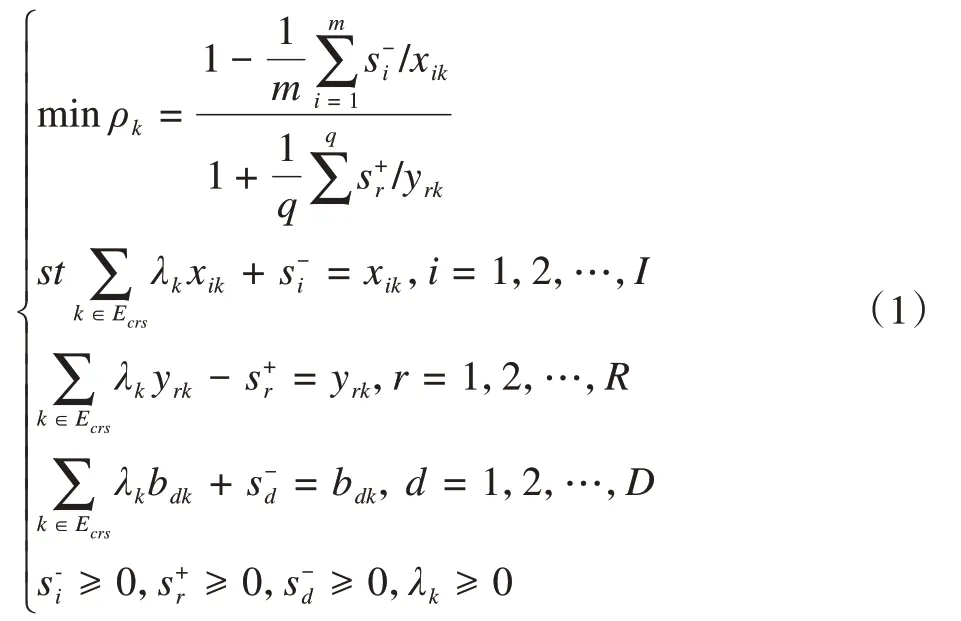
公式（1）中，xik、yrk和bdk分别表示第k个DMU 对应的投入，期望产出和非期望产出。、和为投入，期望产出和非期望产对应的松弛变量。λj表示各DMU 的权重，若，表示生产技术处于规模报酬可变状态，去除该条件，表示生产技术处于规模报报酬不变状态。ρk表示第k个决策单元的技术效率值。

（2）基于SBM-U-DEA进行MinDS-U-DEA模型前沿面的构造。MinDS-U-DEA 模型的可能性生产集表示如下：

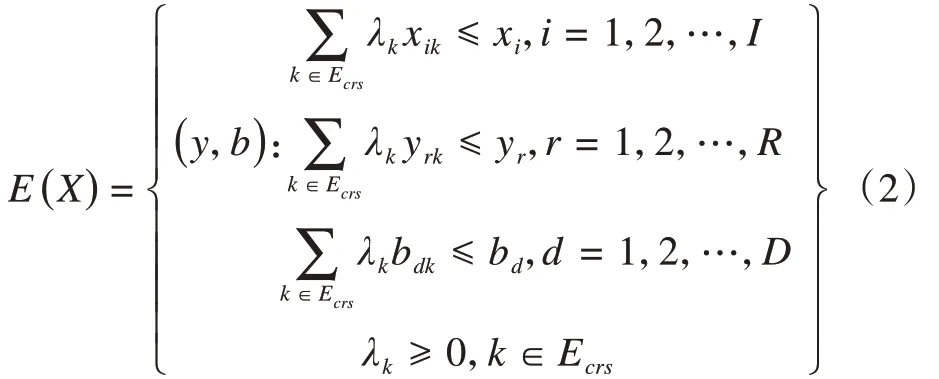
在公式（2）中，Ecrs为MinDS-U-DEA 模型的初始参考集，此外，我们假设vi、ur和βd分别表示投入、期望产出和非期望产出的权重。M是一个足够大的正数。则MinDS-U-DEA的模型如下：

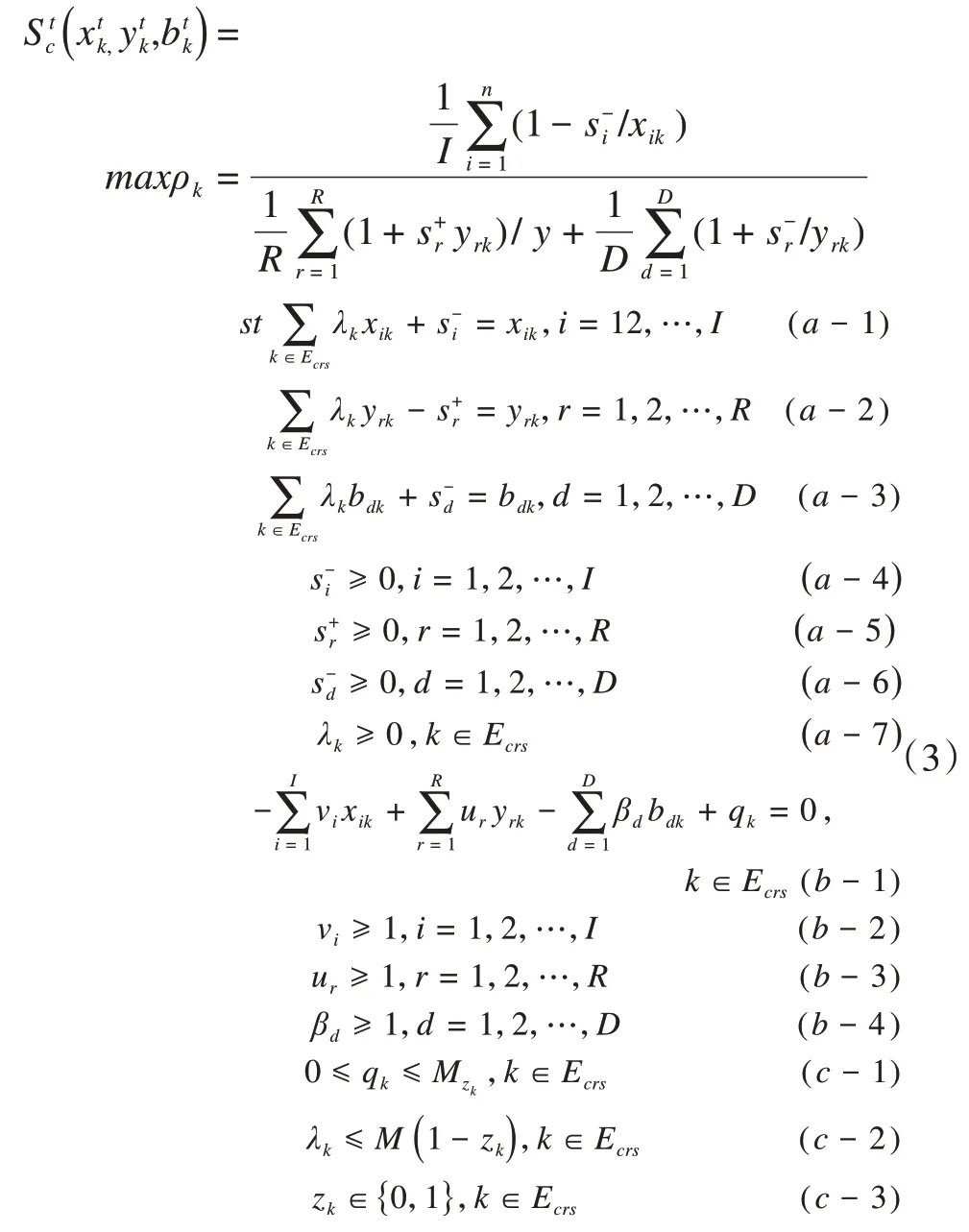
MinDS-U-DEA 模型由目标函数和3个约束组成，约束a、b、c为混合整数线性约束。它参考同一个超平面的基准。zk∈{0,1}，若zk= 0，则qk= 0，λk≤M，DMUK为参照集；若zk= 1，则qk≤Mzk，λk= 0，DMUK不是参照集。

1.2 MinDS-U-M指数

Malmquist指数是基于传统DEA 模型衡量决策单元动态效率的重要方法，根据Chung 等人的研究，结合MinDS-U-DEA 模型构建了包含非期望产出的全要素生产率指数（MinDS-U-M）模型，公式如下：

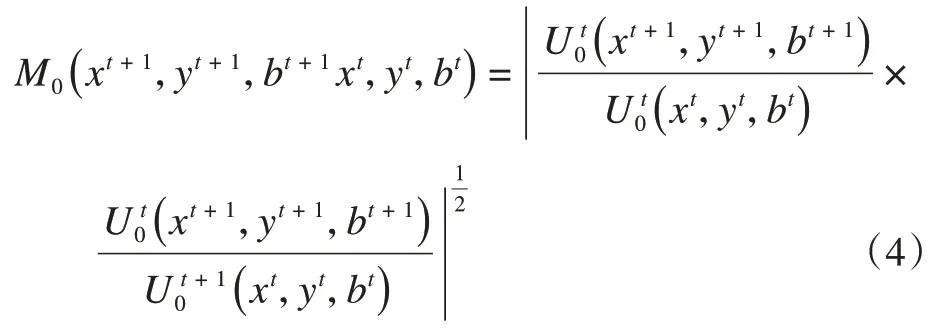
公式（1）中，(xt,yt,bt)和(xt+1,yt+1,bt+1)分别是两个时期的技术效率值；(xt+1,yt+1,bt+1) 和(xt,yt,bt)是在两个时期的混合期间的技术效率值。将公式（4）其进一步分解：

1.3 指标选取和数据来源

指标选取的科学性是进行效率评价的本质要求，应满足以下两个要求：一是指标要具有客观性、代表性和可量化的特征；二是指标数量要达到科学合理的标准，投入和产出指标个数应构成max{m×s,3(m+s)}≤n的数值关系。另外，综合分析各省能源效率现有状况及已有成果，本文选取如下指标：

（1）能源投入。

以考察期间各省能源消耗总量来衡量，单位万吨标准煤。

（2）劳动力投入。

劳动力通常以有效时间内实际参与生产过程的就业人数来表示，因此本文选取各省考察期间年末就业人数来衡量劳动力投入。

（3）资本投入。

以往研究多采用永续存盘法估计资本存量作为资本投入，因此，本文借鉴单豪杰[26]的计算方法，取折旧率为10.96%，并以2000为基年计算2000～2017年期间的资本存量。

（4）期望产出。

经济活动中要素投入的直接收益，以考察期间各省的国内生产总值来衡量，单位亿元，并将各省历年GDP通过平减指数调整为2000年价格。

（5）非期望产出。

本文借鉴张志雯[27]，采用碳排放系数法，将能源消耗总量通过各种能源的碳排放系数来估算CO2的排放量。计算公式为：

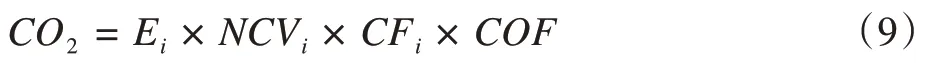
其中，i为能源种类，本文选取原煤、焦炭、原油等8 种能源；Ei为各省第i种能源消费量；NCVi为《中国能源统计年鉴》附录中各能源的平均低发热量；CFiCO2排放系数，COF为碳氧化率。

文中原始数据均来自历年《中国统计年鉴》、《中国能源统计年鉴》以及各地区的统计年鉴。

2 实证分析

2.1 不同指数结果的比较分析

由表1可知，与不考虑碳排放的MinDS-M 和SBMM 模型相比，考虑碳排放的MinDS-U-M 和SBM-U-M 模型测量的中国省际全要素生产率指数都有不同程度的下降，不考虑碳排放将导致对能源全要素生产率的高估。另外，由表2可知，经Wilcoxon 带符号秩检验MinDS-U-M 模型和SBM-U-M 模型的测量结果之间，以及MinDS-M 模型和SBM-M 模型的测量结果之间存在显著差异。这是因为MinDS 模型对SBM 模型缺点的修补，减小了决策单元的投入松弛变量。因此，MinDS-UM 和MinDS-M 模型分别优于SBM-U-M 和SBM-M 模型。此外，考虑碳排放的MinDS-U-M 模型和不考虑碳排放的MinDS-M 模型的测量结果，以及考虑碳排放的SBM-U-M 模型和不考虑碳排放的SBM-M 模型之间存在显著差异。这些关系表明考虑碳排放的必要性和重要性。因此，下文将重点分析考虑碳排放时MinDS-U 模型的测量结果。

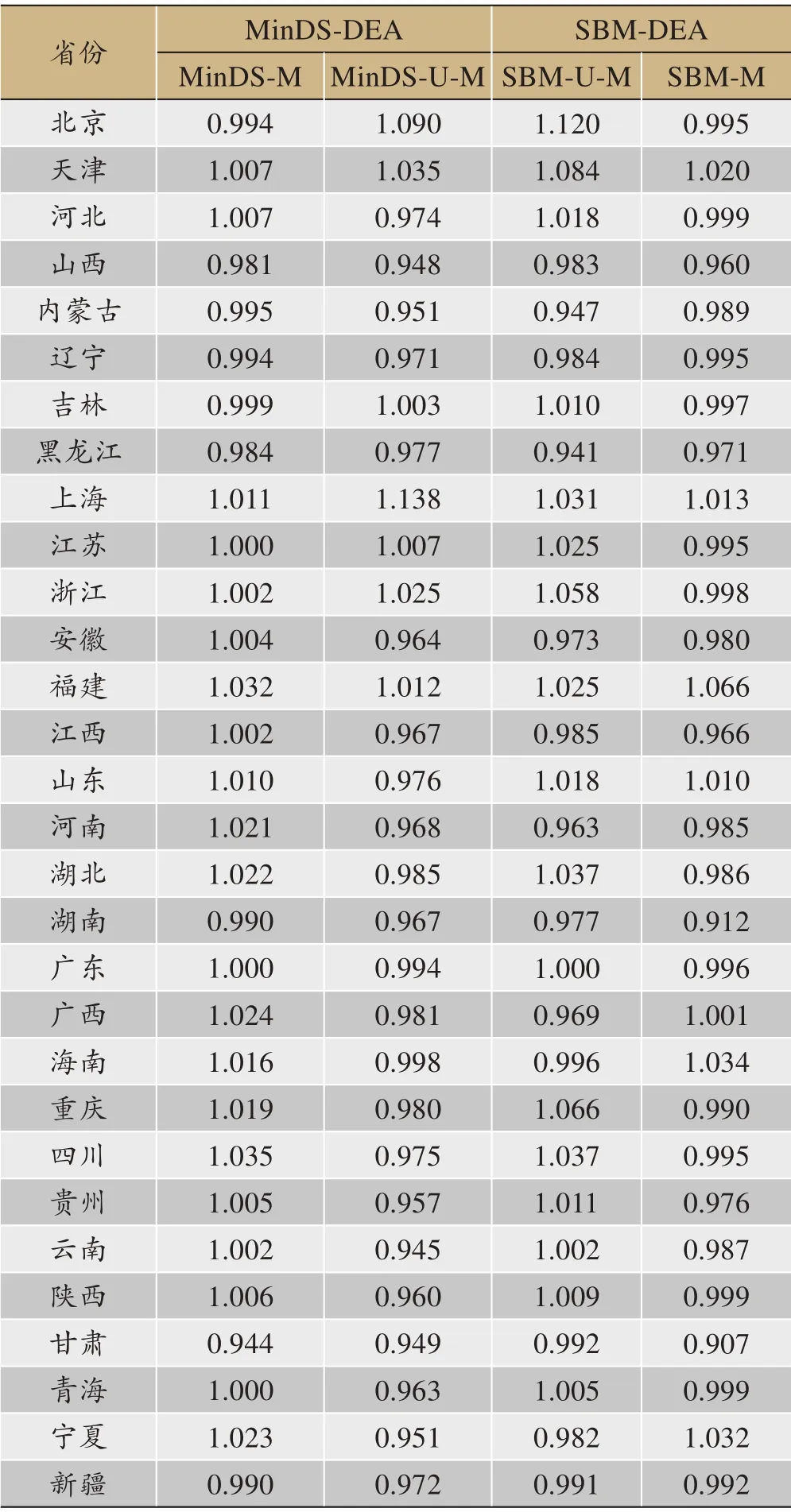
表1 不同模型能源全要素生产率结果

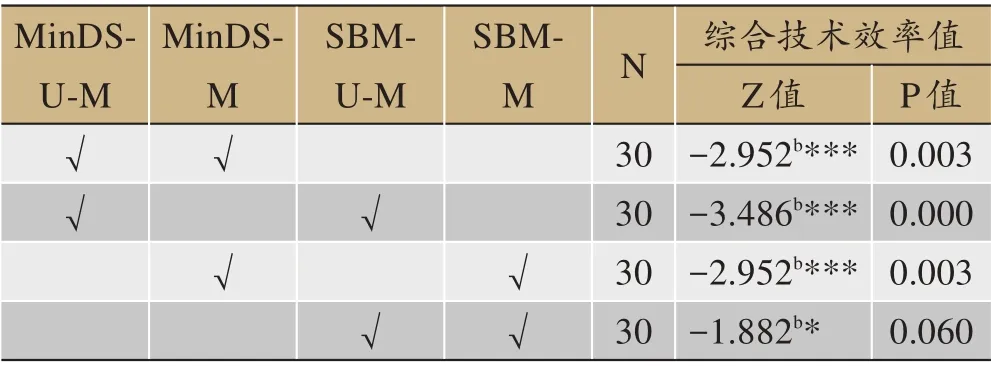
表2 Wilcoxon带符号秩检验结果

2.2 MinDS-U-M指数结果分析

2.2.1 中国省际全要素能源利用效率时间序列分析

由表3可知，我国能源全要素生产率指数（MI）与技术进步指数（TC）的变化趋势一致，整体呈现小幅上升趋势。在跨期对比数据中：2012～2013年、2014～2015年、2015～2016年和2016～2017年的全要素生产率呈现不同幅度的提升，其余年度均为下降。明显注意到，2012年为下降转为上升的一个节点。2012～2017年间我国能源全要素生产率为1.006，平均上升了0.6%，其原因与2011年国家出台“十二五”规划有关（包括《国家能源科技“十二五”规划》、《“十二五”节能减排综合性工作方案》等相关政策）。从要素增长结构来看，2012～2017年期间，TC指数年均增长1.8%，说明科研创新水平有所提高，存在创新效应；规模技术进步（STC）指数和纯技术进步（PTC）指数年均增长分别为1.7%和0.2%，说明主要受益于规模技术的提升。然而，规模效率（SEC）指数和纯技术效率（PEC）指数年均下降分别为0.9%和0.2%，两者均抑制了综合技术效率（EC）指数的增长。技术效率指数低是导致我国近年来省际能源利用水平不高的主要原因，说明相对于能源创新体系、技术进步和管理，我国对于能源科研投入的利用能力和管理水平有待进一步提高。

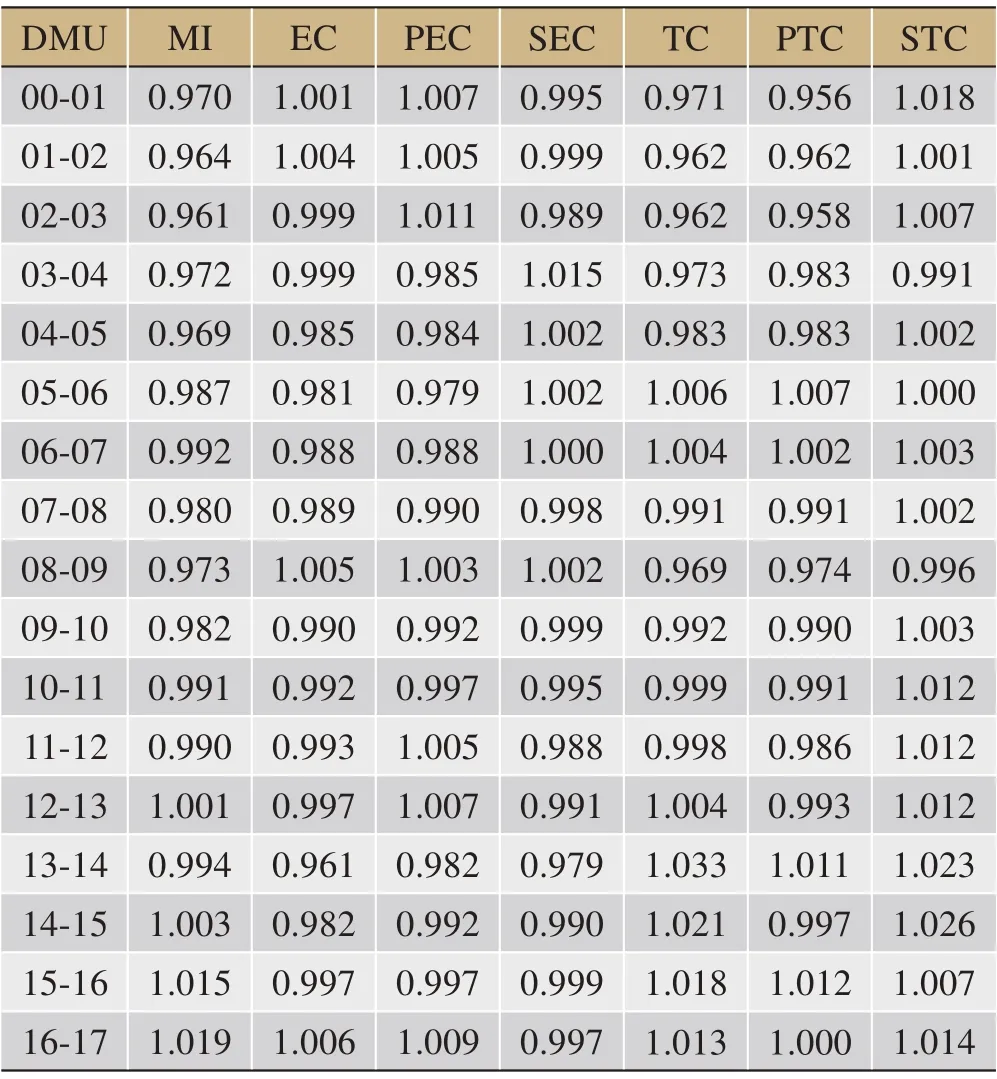
表3 我国整体全要素能源利用效率

2.2.2 中国省际能源全要素生产率区域异质性及发展模式分析

进一步考察我国能源全要素生产率区域特征，结果如表4所示。从分地区看，全要素生产率指数（MI）东部>东北>中部>西部，仅有东部地区的能源全要素生产率超过了1，其增长主要由综合技术进步提供，综合技术效率指数（EC）为0.998，处于能源制度保障和管理状态不佳，主要是因为规模效率不经济。与东部地区相比，东北及中西部地区规模技术进步（STC）指数值均大于东部地区，但纯技术进步（PTC）指数远远落后于东部地区，导致拉低了综合技术进步（TC）指数，且均未超过1；另外，东北及中西部地区纯技术效率和规模技术效率指数值也均未超过1，抑制了综合技术效率（EC）的增长。整体来讲，地区及各省份的全要素生产率较低主要源于综合技术技术效率和纯技术进步共同作用的结果。

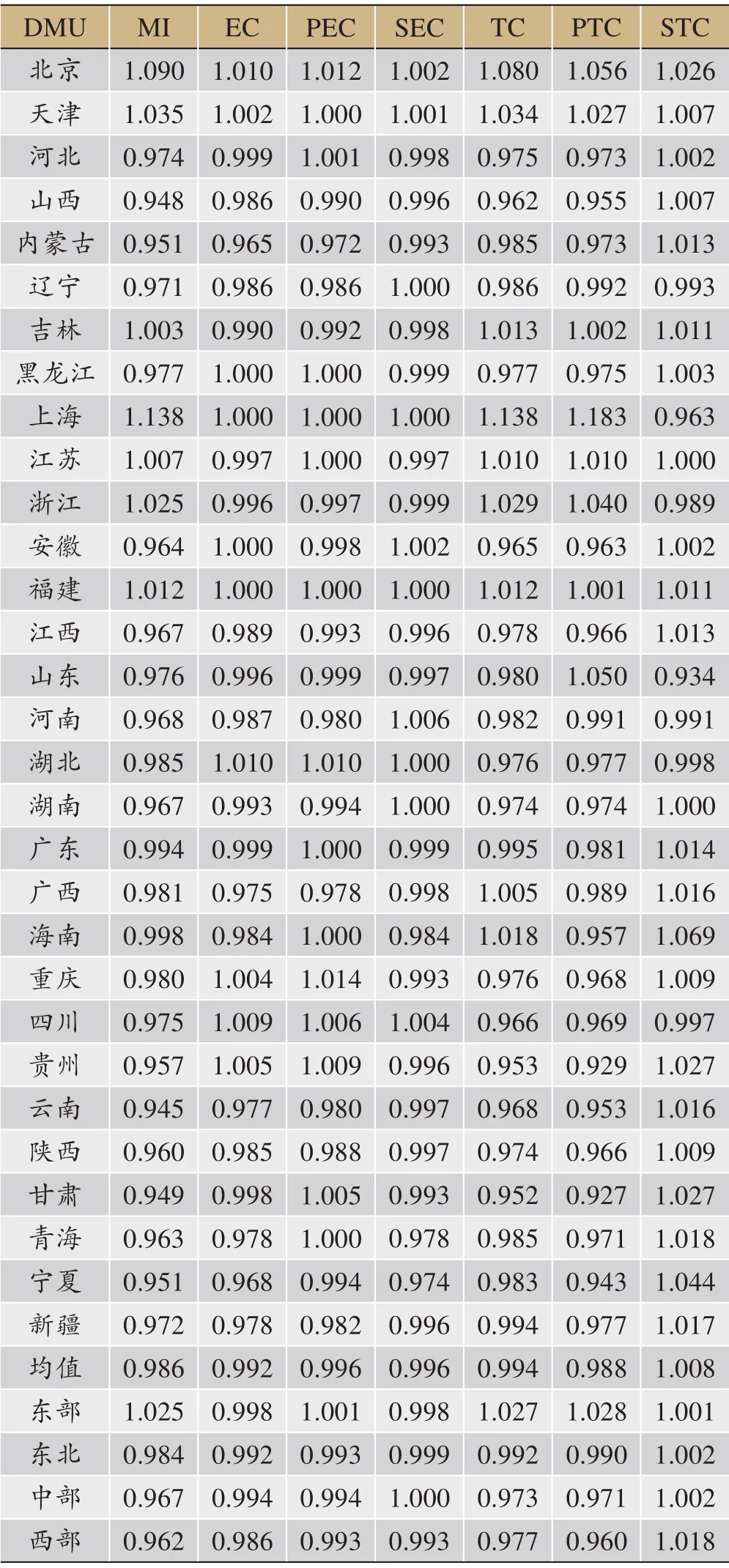
表4 2000～2017年我国各省份年均全要素能源效率指数及其分解

将各地区全要素生产率指数按照MI、EC和TC进行模糊聚类分析，考察中国能源全要素生产率增长模式，如表5所示。整体来看，一方面，在考察期间，MI指数超过1 的省份有7 个，仅占总样本的23.3%。在Ⅰ类中，北京、天津、上海和福建的TC 指数和EC 指数均大于1，创新效应和追赶效应并存（属于双高增长模式），表明这几个省份能源综合利用效果最好，能源效率保持良好的上升发展趋势。在Ⅱ类中，虽然EC指数小于1，缺失追赶效应（属于创新驱动增长模式），但技术进步指数的提升掩盖了技术效率的下降，从而拉动了MI 指数的增长，从侧面讲，该类省份的科技创新水平对能源利用效率的提升有强大的推动作用。另一方面，MI指数小于1 的省份占总样本的76.7%。在Ⅲ类中，技术效率是增长趋势，不存在创新效应（属于效率驱动增长模式），这类省份的能源全要素生产率较大程度上受科技创新水平的约束。Ⅳ类省份的技术效率指数和技术进步指数均小于1（属于双低增长模式），说明这类省份需在技术应用和技术创新两个方面同时加强改进。另外，广西和海南没有归并到上述四类，同Ⅱ类相似，但MI 指数小于1，在较大程度上受技术效率的影响，表明了其技术利用和管理能力较低，基于影响因素是可控制的，所以通过优化资源利用结构，改善基础设施条件可以进一步提升技术效率，从而提高能源全要素生产率。整体而言，中国省际能源全要素生产率增长模式并不理想。

3 结论及建议

本文首先采用2000～2017年面板数据，运用MinDSU-M模型对我国30个省份的能源效率进行了动态分析，并将不同指数测算的全要素能源利用效率进行比较，结果表明：①与不考虑碳排放的MinDS-M 和SBM-M 模型相比，考虑碳排放的MinDS-U-M 和SBM-U-M 模型测量的中国能源全要素生产率指数都有不同程度的下降，不考虑碳排放将导致对全要素生产率的高估，碳排放对我能源全要素生产率具有显著影响；②我国能源全要素生产率指数与技术进步指数的变化趋势一致，整体呈现小幅上升趋势，2012年以来，我国能源全要素生产率为1.006，年均上升了0.6%。③我国东部、中部、西部和东北地区的能源利用效率存在显著差异，其中东部、中部、西部和东北部能源全要素生产率指数的年均增长率分别为2.5%、-1.6%、-3.3%和-3.8%，整体来讲，地区及各省份的全要素生产率较低主要源于综合技术技术效率和纯技术进步共同作用的结果。④仅有4个省份追赶效应和创新效应并存，分别北京、天津、上海和福建，属于双高增长模式；5个省份为单一的创新驱动增长模式，分别是吉林、江苏、浙江、广西、海南；黑龙江、安徽、湖北、重庆、四川、贵州为单一的效率驱动增长模式；其余15个省份均为双低增长模式，综合来说我国省际能源全要素生产率增长模式并不理想。

基于以上结论，给出以下建议：①推进能源绿色低碳发展。通过产业结构调整和可再生能源的开发，降低煤炭消费比重。进行价格机制改革，完善管道运输基础设施，降低成本，提高天然气、风电、太阳能等能源消费比重，构建高效、绿色的社会用能模式。②优化资源配置和提升能源管理利用水平。在我国地区间能源效率显著差异下，东部地区应提升对中西部地区的开放水平，通过政府、企业、高校之间的合作等方式主动输送高水平人才和先进的要素管理理念；中西部地区以及东北地区应积极主动加强与东部地区人才、技术交流强度，积极引进相关高技术人才，学习先进的能源管理技术经验，促进地区间生产要素的合理流动。③提高技术转化效率和能源技术管理水平。各地区加大科技财政支持力度，提供良好的政策环境，完善能源技术保障制度，从而推进技术成果转化以及提高技术利用效率，保障技术进步和技术效率共同推进，优化我国省际能源全要素生产率增长模式；另外，合理控制能源要素投入，在现有规模下充分发挥资源优势。

表5 2000～2017年各地区全要素能源效率指数分类