基于Matlab永磁无刷直流电动机调速系统的仿真研究*

郭志坚，张岳贤

(山西工程技术学院，山西 阳泉 045000)

0 前言

近些年，随着半导体开关器件的高速发展，高性能永磁材料日益普及，永磁同步电机也被广泛应用于各个工业领域；它具有谐波少，转矩精度高，体积小，重量轻，不存在励磁损耗问题，能够有效地解决直流电动机机械式换向器和电刷所造成的火花问题，因此，对于性能和精度要求较高的伺服调速系统，应用尤为广泛。相比于一般的交流电动机，其定子绕组与之相同，但转子磁极使用永久磁铁，故转子磁链是固定的，所以其动态数学模型(电压方程、磁链方程和转矩方程)较简单，且无需计算磁链的观测模型，控制也较简便。

根据驱动电流的形式，永磁同步电动机可分为：正弦波永磁同步电动机(PMSM)和梯形波永磁同步电动机，后者也称无刷直流电动机(BLDCM)。相比于前者，无刷直流电动机的反馈检测装置和控制方法比较简单，能够充分发挥电机和逆变器各自的优势，具有明显的优越性，并且效率高，运行可靠，便于维修，具有优良的调速和起动特性，已被应用到各个领域。本文重点研究无刷直流电动机的调速系统[1]。

1 永磁无刷直流电动机调速系统

1.1 无刷直流电动机的组成

针对他控无刷直流电动机调速系统造成的失步问题，采用自控变频的方式，能够完全消除系统的失步现象，通过转子的位置，直接控制PWM逆变器的输出电压或者电流的相位，使得功率角小于π/2[4,5]。

在电动机的轴端安装一台转子位置检测器BQ，获得转子位置信号，并控制变频装置，以确保转子转速和供电频率是同步的。如图1所示，它包括五部分：不可控整流器，转子位置检测器BQ，PWM变频器UI，控制器和同步电动机MS。

图1 PWM控制的无刷直流电动机的调速原理

1)转子位置检测器BQ。能准确检测转子磁极的位置，以此来调整PWM变频器输出电压信号的频率及相位，使得电机的功率角θ小于π/2。PWM变频器输出频率随着转速同步改变，根本上杜绝失步问题，确保电动机能够稳定运行。

2)不可控整流器。为了在基频以下实现电压频率协调控制，还需要加入可控的直流电压源，改变电压即可改变转速，变频器的输出频率自动跟随转速，实现频率的控制。

3)PWM变频器。为了简化系统的结构，采用PWM变频器，既完成变频，又实现调压。可控直流电源可选用不可控整流装置，或着由直流母线直接供电，这样仅选用一套可控功率单元，大大地简化了系统的结构。

4)无刷直流电动机。把永磁同步电动机和逆变器、转子位置检测器BQ合起来，采用电力电子逆变器和转子位置检测器作为电子式换向器，就可以看作成一台无刷直流电动机。

采用集中整距绕组，输入方波电流，其转子选用瓦形磁钢，气隙磁场也是梯形波；转子上的励磁使用永磁体，为了便于直接输入交流电，电枢位于定子上。

1.2 永磁无刷直流电动机的工作原理

三相桥PWM变频器供电的Y型绕组永磁同步电动机的等效电路如图2所示。Ud为不可控整流输出的直流电压，其值恒定不变。

图2 永磁无刷直流电动机的等效电路

当转子永磁体处于图3(a)时，获得转子转速的信号，并将转速信号转换成相应的电压信号，再经过三相桥逆变电路，使得全控型器件V1和V6导通，此时，电动机定子绕组从A相流入，B相流出，在电机内部产生磁势FA，进而产生磁场,定子和转子通过磁场互相作用，产生电磁转矩，使得电机转动，转向即为磁势的旋转方向。电流的具体流向为：电源正级→全控器件V1→电机定子绕组A相→定子绕组B相→全控型器件V6→电源负极。当转子转到图3(b)所示位置(60°电度角)时，开关器件V6截止，V2导通，此时V1仍然处于导通状态。电动机定子绕组从A相流入，C相流出，在电机内部产生合成磁势FA，定子和转子磁场通过电磁感应，产生电磁转矩，继续拖动转子顺时针旋转。电流的具体流向为：U+→V1→A相→C相→V2→U-，如此循环。

图3 永磁无刷直流电动机工作原理图

当转子按顺时针每转过π/3，全控型开关器件的导通顺序：V1→V2→V3→V4→V5→V6→V1。根据上述分析：转子磁场随着合成磁场顺时针旋转，但空间上定子合成磁场的旋转是断续的，每隔π/3跃变一次，也就是定子磁场的方向随着逆变器中电流的方向变化而变化。因此，无刷直流电动机存在六个磁场,且每个磁场和逆变器中电流两相导通是互相对应的，属于120°导电方式。永磁无刷直流电动机的三相绕组和各开关器件导通次序如表1所示[3]。

表1 三相六状态绕组和开关导通表

无刷直流电动机的电动势也呈现梯形波，通过变频器输入与电动势完全同步的2π/3矩形波电流，以A相为例，其波形如图4所示。

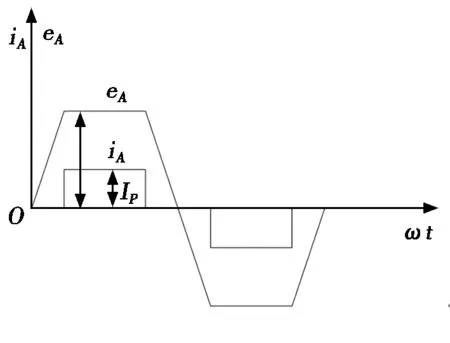
图4 A相的电动势和近似的电流波形图

尽管各相电流的波形都是矩形波，逆变器中开关器件易控制，但各绕组都存在电感，导致换相时电流不能突变，实际中的电流波形类似梯形。因此，转子的电磁功率也是梯形波，且平均电磁转矩在每次换相时会有所降低。PWM变频器每隔π/3进行一次换相，相应的转矩波形就会波动一次，造成转矩脉动，直接影响电机的性能[6]。

2 永磁无刷直流电动机的数学模型

为了简化数学模型，假设：1) 电机三相定子绕组采用Y型接法，且完全对称；2) 空间上的气隙磁通是矩形波；3) 采用三相六状态的导通方式；4) 磁路处于不饱和状态，忽略磁滞和涡流损耗。

由图2可知，永磁无刷直流电动机的电压方程表示如下：

(1)

式(1)中uA、uB、uC为三相输入电压；iA、iB、iC为三相电流；eA、eB、eC为三相电动势；Rs为定子绕组每相电阻；Lσ为定子绕组各相漏磁通所对应的电感。

如果图3中电流峰值为Ip，电动势的峰值为Ep，不换相时，逆变器中仅有两相是导通的，且电机的两相绕组是串联的，则电磁功率为Pm=2EpIp。电磁转矩为：

(2)

式(2)中ψp为梯形波励磁磁链的峰值；wm为电源角频率；w为电动机转子旋转角速度。

忽略换相过程和PWM调制产生的时变和非线性因素的影响，当图2中的开关器件VT1和VT6导通时，A、B两相导通，而C相截止，则iA=-iB=ip，iC=0，且eA=-eB=Ep，由式(1)可得无刷直流电动机的电压方程为：

(3)

式(3)中，(uA-uB)为A和B两相间的平均线电压。

当采用PWM控制时，占空比记为ρ，则uA-uB=ρUd，式(3)化简为：

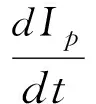
(4)

其对应的状态方程为：

(5)

由电机拖动理论可知：

Ep=keω.

(6)

(7)

(8)

根据式(5)～(8)，推出无刷直流电动机的状态方程为：

(9)

在推导过程中，由于忽略了一些时变和非线性的因素的影响，实际上会导致电机转矩脉动，甚至会影响正常运行，因此，为了解决这些问题，加入转速调节器ASR，且为带积分和输出限幅的PI调节器，其中PI调节器可参考直流调速系统的工程方法进行设计，首先将实际的调速系统化简为典型的I型或II型系统，然后直接利用典型系统的公式和图表，最后计算出PI调节器的参数，以供仿真实验进行参考。

3 无刷直流电动机调速系统建模与仿真

3.1 无刷直流电动机调速系统的仿真模型

无刷直流电动机调速系统的仿真模型，如图5所示，调速系统包括：永磁同步电动机模块、三相桥逆变器模块、PWM发生器模块、电源、控制器模块和PI调节器。在电机模块中，励磁类型设置为梯形波Trapezoidal；逆变模块中采用三相桥电路，选择全控型开关器件IGBT，通过电动机转子位置角和PWM输出的脉冲，经过控制器模块的运算，获得IGBT的6路控制脉冲，控制器件的开通和关断，调节占空比来调节电动机的电压，实现调速。给定转速设为2 000 r/min，与转速反馈量进行比较，通过转速PI调节器，最终实现转速调节[7]。

控制器模块Controller内部结构，如图6所示。首先检测出转子位置角，然后经过Rounding Function、Relational Operator等模块，每隔π/3获得一个矩形波脉冲(周期为2π，脉宽为2π/3)，再结合PI调节器的输出信号经过与门运算得到IGBT的6路控制信号。

图5 无刷直流电动机调速系统仿真模型

图6 控制单元Controller的仿真模型

3.2 仿真结果和分析

电动机的参数：极对数ρ=2，定子电阻Rs=4.765 Ω，定子电感Ls=0.0085H，励磁磁通0.1848Wb，转动惯量J=0.008kg·m2，励磁脉冲宽度120°；转速调节器的参数：比例系数kp=11.7，积分系数ki=140。永磁无刷直流电动机变频调速系统的仿真波形，如图7所示。其中图7(a)为电动机的转速仿真波形，电动机带恒转矩负载，TL=1.5 N·m时满载启动，调节时间约为0.005 5 s，超调量约为9.8%，尽管有超调量，但影响不大，可忽略，调节时间断，转速波动小，表明电动机的动态跟随性能较好。图7(d)为电动机A和B之间的线电压仿真波形。图7(b)为定子A相的电流仿真波形，呈现梯形波，且电流有纹波。图7(c)为电磁转矩的波形，转矩脉动较大，主要是电压采用PWM控制，在2π/3导通区间内有电流纹波，直接导致转矩出现脉动。

图7 永磁同步电动机调速系统仿真波形

4 总结

本文研究永磁无刷直流电动机变频调速系统，在分析无刷直流电动机结构和工作原理的基础上，建立系统的数学模型，采用自控变频调速的方式，克服失步现象，利用PI转速调节器，改善调速系统的动态性能。最后在Matlab中，搭建了调速系统的仿真模型，结果表明：永磁无刷直流电动机的调节时间约为0.0055s，超调小，具有良好的动态跟随性能，存在一定的转矩脉动，提高PWM的频率和限制关断相调制占空比可以有效地减小转矩脉动[8]。