考虑软时间窗的多车型车辆配送路径优化
鲍 伟,贾江鸣,李湘生,周庆红
(1.浙江理工大学 机械与自动控制学院,浙江 杭州310018;2.金华市华南汽配有限公司,浙江 金华321000)
0 引言
近年来,物流产业在国家相关政策的扶持下迅速发展,但物流成本仍居高不下。配送作为物流系统的核心环节,在物流成本中的占比超过50%,因此配送成本过高成为了物流成本居高不下的重要因素[1-3]。通过合理地安排车辆进行配送才能有效地降低物流成本。
目前,国内外学者将车辆配送路径优化问题称为VRP(Vehicle Routing Problem)问题,并进行了大量研究。Yin等[4]将解决车辆配送路径优化问题的方法归为两类:精确优化算法和启发式优化算法。吴艳群等[5]根据先验经验设置初始值,再采用模拟退火算法对车辆路径问题进行求解。同时部分学者为降低运输成本对多车型车辆问题进行研究,陈研等[6]以总成本最小为目标,考虑提高车辆满载率、减少出行次数,构建多车型集配货一体化车辆优化模型。王旭坪等[7]加入车型调整策略所构造的邻域搜索算法,用于满足客户对不同车型服务的多样化需求。葛显龙等[8]以车辆运输成本和固定成本最小化为目标,建立出针对超市越库作业的多车型车辆路径优化模型。部分学者们在VRP的基础上考虑时间窗因素的车辆路径问题(Vehicle Routing Problem Time Windows,VRPTM),Malek等[9]提出一种人工蜜蜂搜索算法来提高VRPTM的收敛速度。李珍萍等[10]提出一种求解模型的联合优化遗传算法用于解决多需求混合整数规划模型。李兵飞等[11]提出一种改进的人工蜂群算法用于解决时变VRPTM问题。
综上所述,目前针对VRPTM问题的研究存在模型复杂、算法收敛较慢、依赖先验经验等问题。因此,本文以车辆固定成本、车辆运输成本、等待时间惩罚成本组成的总配送成本最小化为目标,引入软时间窗惩罚函数,建立多车型车辆配送路径优化(Multi-type Vehicle Routing Problem Time Windows,MVRPTM)模型;采用自适应竞争的遗传算法对多车型车辆配送路径优化模型进行求解,其中引入自适应竞争策略来提高算法的收敛速度,采用多车型车辆选择算法来对车型进行选择。最后通过某物流公司的配送算例对模型和算法性能进行评估分析。
1 问题描述与模型建立
1.1 问题描述
某配送中心配备多种车型的车辆且车辆数目充足,某个区域中存在待服务的客户点,配送中心在满足每个客户的需求量和可接受服务时间的条件下,合理安排各种类型的车辆对客户进行配送服务,最终车辆服务完所有客户后返回配送中心。
考虑到实际问题的复杂性和不确定性,对MVRPTM做出基本假设:
(1)配送中心有且仅有一个,且能满足所有客户的货物装载;
(2)车辆从配送中心出发服务完所有客户,最终返回配送中心;
(3)每位客户的货物不允许拆分放置于多辆车;
(4)客户的需求量、服务时间、接受服务时间、客户地图位置信息都是已知的;
(5)车辆运输货物容量小于车辆的容量,且每位客户的需求量小于车辆容量。
1.2 模型中符号和决策变量(如表1所示)

表1
1.3 模型建立
根据问题描述,将以总配送成本最小化为目标,建立带软时间窗的多车型车辆路径优化模型。其中总配送成本包括:车辆固定成本、车辆运输成本、等待时间惩罚成本,并根据问题描述,建立三维装箱约束下的多车型车辆路径组合优化模型见式(1)至式(10):
(a)目标函数

(b)约束条件
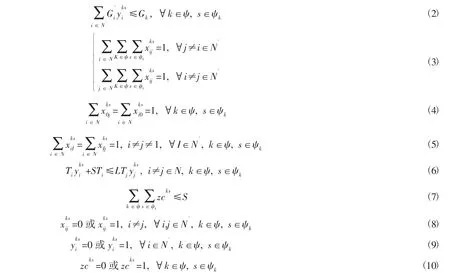
式(1)表示最小化总配送成本的目标函数;式(2)表示车辆运输货物的容量小于车辆的容量;式(3)表示每位客户的需求货物不能拆封放置于多辆车上;式(4)表示每辆车都从配送中心出发,最终返回配送中心;式(5)表示车辆驶向某客户点,则必须从该客户点离开;式(6)表示车辆要在最大时间窗内对客户进行配送服务;式(7)表示调度车辆数不超过配送中心车辆总数;式(8)至式(10)表示决策变量。
2 自适应竞争的遗传算法求解MVRPTM
MVRPTM的实际应用问题属于NP-hard难题,通常采用启发式算法求解。遗传算法本身从问题解的串集开始搜索,采用概率变迁规则来指导搜索方向,优化过程中同时处理多个个体,并对搜索空间中的多个解进行评估有利于全局择优,适用于对组合优化问题的求解,但存在收敛速度慢或过早收敛等问题。局部搜索算法从一个初始解开始通过邻域搜索,选择最优邻域解做为下一迭代的初始解,经过多次局部搜索,有利于提高解集的质量[12]。本文利用局部搜索算法的优势,在遗传算法中引入自适应竞争策略来提高算法获取优秀解的能力。
自适应竞争的遗传算法流程图如图1所示。首先遗传算法生成初始种群,经过自适应竞争策略对种群进行优化,给出客户反向配送顺序,再通过多车型车辆选择算法和构造式启发式算法给出多车型车辆的装箱方案和多车型车辆的配送方案。最后对自适应竞争的遗传算法进行迭代循环,直到满足终止条件。

图1 自适应竞争的遗传算法流程图
2.1 染色体的编码与解码
本文采用自然数编码,用0表示配送中心,1,2,…,n表示客户点,染色体编码如图2(a)所示,每条染色体表示客户装载的顺序。图2(b)表示染色体解码后的个体,每个个体表示车辆对客户进行配送服务的顺序,第一辆车从配送中心0出发,依次服务客户3,1,2,10然后返回配送中心0,第二辆车从配送中心0出发,依次服务客户4,6,5,然后返回配送中心0,第三辆车从配送中心0出发,依次服务客户8,9,7,然后返回配送中心0。

图2 染色体编码与解码示意图
2.2 适应度函数
本文将多目标函数转化为以总配送成本最小化的单目标函数的倒数作为适应度函数,适应度函数越高遗传到下一代的概率越高。
2.3 选择算子
本文采用Holland提出的轮盘赌策略,根据每个染色体适应度的比例来确定该染色体被选择的概率,依照选择概率选择个体直到种群数达到M。每次生成的新种群结合精英保留策略,用上一代最优个体替换新种群中适应度函数最差的个体。
2.4 改进的交叉算子
本文的交叉算子是对传统的部分映射交叉算子进行改进。当两个被选择的染色体相同时,仍能产生新个体,避免丢失种群多样性,陷入局部最优。改进交叉算子示意图如图3所示,基本思路为:
Step1:以概率Pc选择两个父代parent1、parent2,随机产生两个交叉点a、b,同时产生交叉基因片段Fab;
Step2:对染色体parent1、parent2进行基因前移,直到交叉点a为首个染色体基因;将parent1中发生交叉的染色体基因片段Fab逆序插入到前移后的染色体parent2末尾;将parent2中发生交叉的染色体基因片段逆序插入到前移后的染色体parent1头部;
Step3:删除与交叉片段基因相同的部分,得到子代offspring1、offspring2。
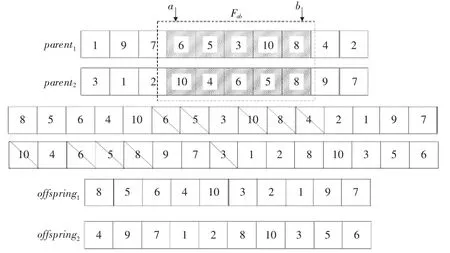
图3 改进交叉算子示意图
2.5 变异算子
本文采用两点互异的变异算子,以一定的概率Pm随机选择一条染色体,随机生成两个变异点,将变异点基因互换得到新个体。
2.6 自适应竞争策略
自适应策略根据当前种群变化的状态来自适应调整竞争状态的开启与停止,以此来平衡搜索效率与种群多样性之间的关系。竞争策略开启阶段将交叉阶段产生的子代与父代进行比较,仅对优于父代的子代进行保留,加强优秀染色体片段的遗传性,提高算法的收敛速度;竞争策略关闭阶段,每次迭代引入新种群,以提高种群的多样性。
(a)竞争策略停止准则。如果当前种群最优解优于上一代种群最优解,重置自适应竞争状态s;否则自适应竞争状态s次数加1,直到自适应竞争状态s达到阈值时停止竞争策略。
(b)竞争策略再开启准则。竞争策略停止状态下,每次迭代向种群中引入M新种群数,当竞争策略关闭状态下,种群生成次数占当前总种群生成次数的比例系数达到ζ时,开启竞争策略,并重置自适应竞争状态s。
(c)交叉阶段进行竞争策略。在竞争策略开启阶段,对交叉算子生成的子代进行判断,如果存在某个子代优于父代,则保留本次子代并重置竞争次数;否则,自适应竞争状态o加1,直到自适应竞争状态o达到阈值时输出最优解并自适应竞争状态o。
2.7 多车型车辆选择
多车型车辆选择算法应用了深度优先搜索的思想,如图4所示。各种类型车辆按照类型号从大到小排序,且车辆容积由大到小顺序调用,即后面调用车辆的容积不大于前面调用车辆的容积,假设排序为V1,V2,V3,…,Vk。其中第一辆车调用的可能为V1,V2,V3,…,Vk,当第一辆车的车型为V1时,第二辆车的车型可能为V1,V2,V3,…,Vk,若第一辆车的车型为V2时,第二辆车的车型可能为V2,V3,…,Vk,依此类推进行车辆选择。基本流程如下:
Step1:按照深度优先搜索方式,对配送货物进行装载;
Step2:若车辆无法再装载剩余客户的货物,则调用下一辆车;若所有客户的货物都装载,则生成可行装载方案;
Step3:进行下一次深度优先搜索装载,直到深度优先搜索完成;
Step4:比较所有深度优先搜索生成的装载方案,选择最优的装载方案。

图4 多车型车辆选择算法示意图
3 算例分析
3.1 数值实例
针对某物流公司2018年10月的实际业务数据。物流配送中心分别对19位客户进行配送服务。其中配送中心共有3种类型的车辆(每种车型5辆,共15辆)给予租赁。车辆规格信息、客户信息分别如表2、表3所示。若车辆在服务时间窗前到达客户点的等待时间惩罚成本0.3元/分钟。
根据上述案例对模型进行仿真,以迭代次数为算法终止标准,设置模型参数如下:种群规模M=50,迭代次数T=5 000,交叉概率Pc=0.85,变异概率Pm=0.1,设置自适应状态o的阈值α=20,自适应状态s的阈值β=13,竞争策略停止阶段种群生成次数占当前总种群生成次数的比例系数ζ=0.3。

表2 物流公司待调度车辆规格
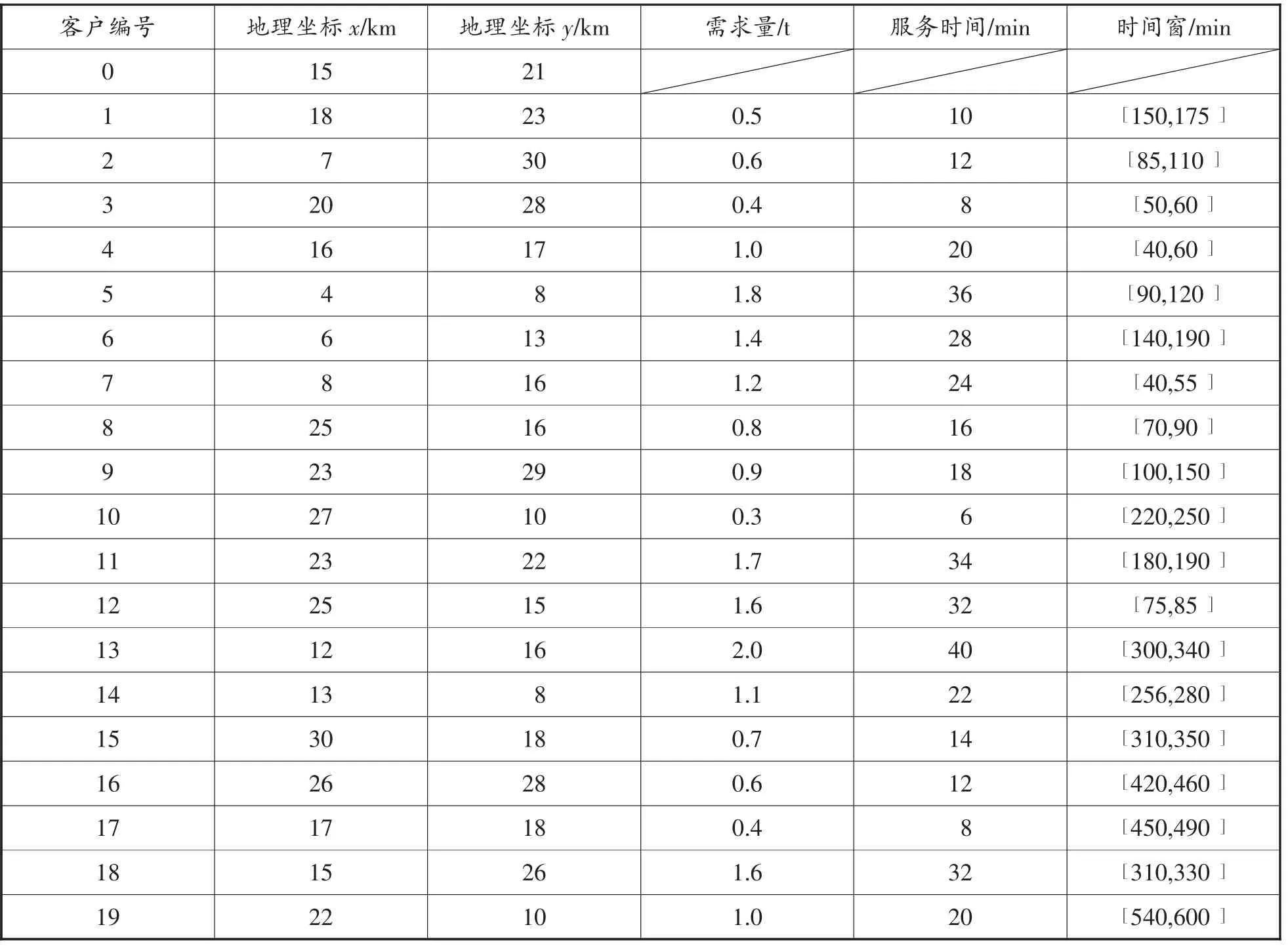
表3 2018年10月部分客户货物信息
试验平台为3.6GHz的AMD 3600处理器、16GB内存的计算机平台实现,最终模型优化结果如表4所示,物流中心安排1辆容积为8t和2辆容积为6t的车辆对19个客户点进行配送服务,总配送成本510.35元;最终的多车型车辆配送路径如图5所示。

表4 采用自适应竞争的遗传算法优化后的结果
图5为多车型车辆配送路径图,数字“0”表示物流配送中心,数字“1,2,…,19”表示客户点。其中不同样式的线条表示不同的车辆,图例中显示所调用车辆的类型。直线表示的配送线路“0-4-2-7-5-6-13-0”由容积为8t的车辆进行配送;虚线表示的配送路线“0-18-3-9-16-11-1-0”由容积为6t的车辆进行配送;点画线表示的配送路线“0-17-12-8-15-10-19-14-0”由容积为6t的车辆进行配送。
3.2 算法实验性能分析
为验证自适应竞争遗传算法对MVRPTM问题的求解性能,将该算法和遗传算法进行对比分析。利用上述案例的数据,设置初始化参数:种群规模M=50,迭代次数T=5 000,交叉概率Pc=0.85,变异概率Pm=0.1,设置自适应状态o的阈值α=20,自适应状态s的阈值β=13,竞争策略停止阶段种群生成次数占当前总种群生成次数的比例系数ζ=0.3。自适应竞争遗传算法和遗传算法迭代图,如图6所示。
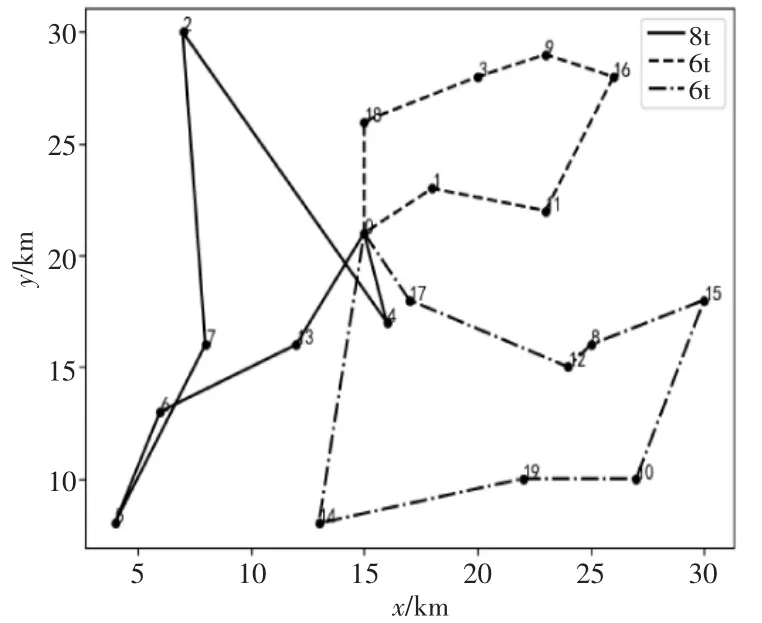
图5 2018年10月多车型车辆配送路径图

图6 自适应竞争的遗传算法和遗传算法迭代图
将上述算法各仿真10次取平均值,自适应竞争遗传算法求解波动相对平稳,算法在622代收敛,总配送成本为510.35元;遗传算法在3 105代收敛,总配送成本为528.74元。自适应竞争的遗传算法收敛代数与遗传算法比较提升5倍左右,最终自适应竞争的遗传算法的总配送成本比遗传算法减少18.39元。
3.3 敏感度分析
在实际货物配送过程,调度不同车型的车辆对总配送成本有影响。本文根据实际物流车辆配送情况,采用多车型车辆配送模式,在一定程度上降低物流成本,提高运作效率。因此车型的使用是影响配送成本的关键,继续采用上述的实例和参数对车辆路径问题进行敏感度分析。求解结果如表5至表8所示。

表5 单采用6t车型配送路径方案

表6 单采用7t车型配送路径方案

表7 单采用8t车型配送路径方案

表8 采用各种车型方案的总路径和总成本对比
由表8可知,采用单车型6t的总配送成本为590.44元,采用单车型7t的总配送成本为528.08元,采用单车型8t的总配送成本为583.11元。随着车型的容积从小到大,总行驶路径逐渐变短,考虑到配送成本,仅采用车型3不一定是配送成本最少的方案。采用多车型配送与采用单6t车型配送相比,装载率提升16.33%,总路径长度减少3.33km,减少成本80.08元;与单7t车型配送相比,虽然总路径长度增加2.99km,但装载率提升4.67%,总配送成本减少17.72元;与单8t车型配送相比,虽然总路径长度增加3.81km,但装载率提升16.33%,总配送成本减少72.75元。因此,通过采用单车型车辆与多车型车辆进行总配送成本对比,可以看出在配送中采用多车型进行配送能更好地降低配送路径,并减少物流的配送成本。
4 结论
本文针对带软时间窗的多车型车辆配送路径优化问题,以车辆固定成本、车辆运输成本、等待时间惩罚成本最小化为目标,建立带软时间窗的多车型车辆路径优化模型。考虑到模型的复杂性,本文引入自适应竞争策略、多车型车辆选择算法设计出自适应遗传算法求解本文的模型。最后以某物流企业的配送为仿真对象进行优化实验,实验结果表明物流企业在对客户进行配送时,采用多车型配送与采用单6t车型配送相比,总路径长度减少2.22%,减少成本13.6%;与单7t车型配送相比,虽然总路径长度增加2.04%,但是总配送成本减少3.36%;与单8t车型配送相比,虽然总路径长度增加2.6%,但总配送成本减少12.48%。且自适应遗传算法与遗传算法相比具有更高的优化精度与优化效率。
模型中考虑多车场、可变油耗、时变车速、交通拥挤等更多实际因素,进一步降低物流成本是下一步研究方向。

