离散傅立叶变换用于非连续工业数据分析

孙学辉 赵 冰 骆 震 孙培健 彭 斌 聂 聪* 邵学广

1(中国烟草总公司郑州烟草研究院， 郑州 450001) 2(河南中烟工业有限责任公司， 郑州 450000) 3(南开大学化学学院， 分析科学研究中心， 天津 300071)

1 引 言

随着大数据时代的来临，科学研究、工业生产、商务活动等诸多领域均出现了大规模的数据增长，如何通过大数据的挖掘和应用产生新的知识和价值已经成为高度关注的热点[1,2]。当前，很多行业和领域都涉及到了大数据问题，例如利用商业大数据进行消费者行为模式的研究，利用医疗大数据进行疾病诊断新方法的研究等等。大数据的突出特点是数量大、产生速度快、数据类型多样和价值密度较低，必须通过数据的深度挖掘才能得到其高的价值，但同时也给数据的分析带来了挑战。

在化学测量学领域，大数据也越来越受到重视[3,4]。化学测量技术和仪器的发展使得化学测量数据迅速增长，已经难以使用常规的统计分析方法直接进行处理。因此，用于大数据分析的化学计量学方法得到发展，建立了针对高维、多类型、时间序列等数据的分析方法[5]。这些方法多为传统的化学计量学方法，如多元统计、多元校正与建模、多元分辨与模式识别等，但在实际应用过程中，往往与信号处理、变量选择、优化算法、数据融合等方法联合，用于相关分析、定量预测、聚类分析与判别分析等，其中基于不同原理的数据分割、样本压缩、分布式计算与共识策略相结合等技术在巨量数据的分析中发挥了重要作用。同时，基于核函数变换的主成分分析和偏最小二乘算法为大数据分析提供了基础算法[6,7]。

近年来，深度学习在大数据分析中的应用日益增加。2019年，Belthangady等[8]对于深度学习在图像恢复和超高分辨成像分析中的应用进行了综述，介绍了深度学习应用于图像重建的最新研究进展，同时也对深度学习面临的挑战，如训练数据的获取、未知结构发现的可能性、不确定图像细节的推断等进行了评述。随着深度学习技术的发展，卷积神经网络在图像生成和图像分析方面得到了应用，如体层摄影图像、磁共振图像以及荧光显微成像，广泛应用于图像修复、卷积与超高分辨率成像、图像着色(染色)、图像分割、聚类分析与表型分析等。深度学习在光谱数据分析中的应用也已有报道，特别是在荧光成像分析、生物医学光谱数据分析等中的应用。有文献建立了一种基于卷积神经网络和长短期记忆神经网络结合深度学习方法用于单分子荧光成像光漂白事件计数数据的分析，获得单分子荧光漂白轨迹，改善了计算效率，提高了分析的准确性，并用于蛋白质复合物化学计量比的自动预测[9]。在近红外光谱研究领域，采用卷积神经网络和长短期记忆神经网络相结合建立了一种深度学习方法用于“情感模型”研究[10]。采用功能近红外光谱测量对人脑血流进行无损检测，检测在受到外部刺激时的光谱变化，然后通过所设计的神经网络建立光谱变化与响应之间的关系。也有文献报道了用于建立近红外光谱定量模型的深度学习方法[11], 设计了包括三个卷积层和一个全连层的网络结构，用于4组开放的近红外光谱数据分析，简化了数据处理步骤，计算结果也得到了明显改善。

本研究提出了一种工业生产大数据的分析方案与方法。对于间歇式、分批次、由多种原料形成产品的工业生产，产品质量的检测一般按照产品的生产批次进行，而原料的检验则按照进货数量和时间进行检验，无论是检验的频次还是检验的时间都不尽相同，产品质量的检验指标和原料的检测数据之间很难具有一一对应关系。因此，难以建立产品质量与原料参数之间的定量模型。本研究将产品的质量指标和原料的检测数据都假定为周期性变化的数据，采用傅里叶变换(Fourier transform, FT)得到各指标和参数的频率信息，并利用逆变换重构相对应的指标和参数，然后再建立质量指标和参数之间的关系模型，用于考察各生产原料对产品质量的影响。

2 数据与分析方法

2.1 数据收集

本研究收集了某卷烟生产过程的工业生产数据，作为产品的质量控制指标，收集了烟气的常规成分含量，即焦油、烟气烟碱、一氧化碳和烟气总粒相物，分别用y1、y2、y3、y4表示。为了研究质量指标与卷烟材料之间的关系，还收集了烟支物理参数(烟支重量、烟支吸阻、总通风率)、滤棒参数(滤棒压降均值)以及卷烟纸参数(卷烟纸定量，即每平方米卷烟纸的重量)，分别用x1、x2、x3、x4、x5表示。所有指标和参数均参照国家标准检测得到，烟气的常规成分含量的测试标准分别是GB/T 19609-2004(卷烟用常规分析用吸烟机测定总粒相物和焦油)、GB/T 23355-2009(卷烟总粒相物中烟碱的测定，气相色谱法)、GB/T 23356-2009(卷烟烟气气相中一氧化碳的测定，非散射红外法)； 烟支重量、烟支吸阻、总通风率和滤棒压降的测试标准是GB/T 22838-2009(卷烟和滤棒物理性能的测定)； 卷烟纸定量的测试标准是GB/T 451.2-2002(纸和纸板定量的测定)。所收集指标和参数的时间跨度为2013年1月1日到2018年12月31日，但各指标和参数数据的采集日期和数据点的多少均不相同，即数据之间无法进行一一对应。因此，无法直接采用这些数据对生产工艺参数对产品质量指标的影响进行研究。本实验所使用的数据中，烟气成分、烟支物理参数、滤棒参数和卷烟纸参数分别有72、1700、1728和80个数据，对于每天对同一指标或参数进行多次检测的情况，采用了平均值进行计算。涉及的数据虽然数据量并不是很大，但收集时间跨度为6年，并且数据的采样密度不一， 采样时间也不同步，因此具备了大数据的某些特征。

2.2 计算方法

FT是一种常用的信号分析方法，最常用于周期性信号分析，考察信号中的不同频率成分。许多波形可作为信号的成分，比如正弦波、方波、锯齿波等，FT采用正弦波作为信号的成分。连续FT用于函数的连续频谱分析，而离散傅立叶变换(Discrete Fourier Transform，DFT)是信号分析的基本算法，把信号从时间域变换到频率域，进而研究信号的频谱结构和变化规律。DFT的正、反变换定义为：

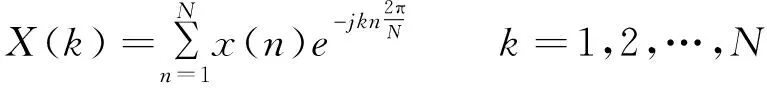
(1)

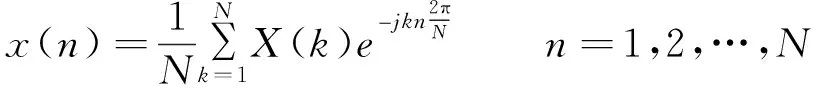
(2)

其中，

(3)

任何连续测量的离散时序信号x(n)都可以表示为不同频率的正弦/余弦波信号的无限叠加，通过FT对测量信号进行分析可以得到信号中不同正弦/余弦波信号的频率、振幅和相位。因此，FT的实质是分析信号中的不同频率成分及它们的相对大小。在实际应用中, DFT一般使用快速傅里叶变换(Fast Fourier transform, FFT)算法进行计算，将DFT计算转化为循环卷积，减少了乘法计算，提高了计算速度。本研究采用MATLAB系统中的FFT函数，使用的是Cooley-Tukey算法[12]。

计算时，首先将各时间上各自独立的控制指标和工业生产参数按照时间顺序排列，然后进行傅里叶分析，得到数据随时间的变化规律，并对数据中最主要的频率成分进行考察，分析各指标和参数的周期性变化规律。然后，采用傅里叶逆变换重构各指标和参数，得到时间上一一对应的指标和参数值，再利用逐步回归方法建立指标和参数之间的多元线性模型，得到对各指标与参数之间的定量模型。

3 结果与讨论

3.1 数据预处理与数据分布

数据预处理往往是大数据分析的第一个步骤，使数据分析适用于后续的计算方法，同时保证数据分析与预测结果的准确性与可靠性, 主要包括数据清理(或称为“数据清洗”)、数据集成、数据归约与数据转换等。本研究的数据包括不同的化学测量值和原材料及产品的物理参数，具有不同的量纲，数值的差异较大。因此首先将数据进行了标准化处理，即将各参数的数值减去其平均值再除以其标准偏差。同时，本研究的数据中各参数或指标在收集时间上具有较大差异，即数据点数、收集时间、收集密度等都不相同。为了便于时间上的一致性，本研究采用“时间数”作为时间量度，即采样时间距公元1年1月1日0时的时间差值，其数值包括整数部分和小数部分，前者表示天数，后者表示时、分、秒等。只采用整数部分，如2013年1月1日对应的数值是735235，而2018年12月31日的数值是737425。

图1是经数据处理后的5个自变量(过程参数)和4个因变量(质量指标)随时间的变化。首先，各参数在数据量上有很大不同，且采样时间并不对应。其次，某些参数(如x1、x2、x3、x4)在2018年期间有一段时间的缺失，需要对这些数据进行补充才能开展后续的研究工作。另一方面，该图展示了生产过程在6年内基本稳定，但存在着一定的波动或变动，如x2存在阶段性的下降现象，x3存在整体上的上升趋势，而4个质量参数均具有比较明显的下降趋势。

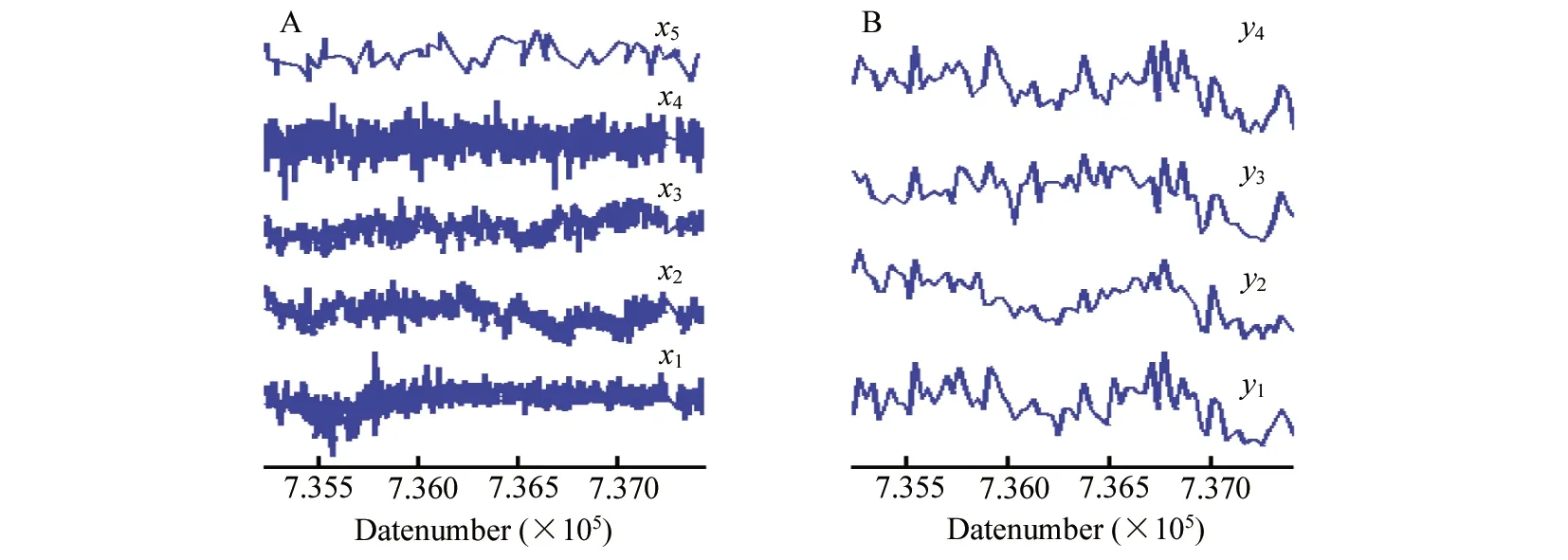
图1 过程参数(A)和质量指标(B)随时间的变动Fig.1 Variation of production (A) and quality (B) parameters with the date of the detection

3.2 数据的周期性分析

为了考察各参数和指标的周期性变化，分别对各参数进行了FT。采用DFT得到的系数如图2所示。由于各参数和各指标的结果具有很高的相似性，图中只显示了过程参数x1和质量指标y1的计算结果。尽管图1显示各参数和指标都具有不同程度的波动，从图2可以清楚地看出，数据的变动无明显的周期性，两图中绝对值最大的系数占所有系数的百分比只有0.12%和2.78%。但是与长周期对应的前几个系数还是相对较大，表明数据在6年的时间里仍然具有单调下降或上升的趋势以及周期在一年以上级别的周期性变化，说明无论是生产原料还是产品都存在着随时间逐渐小幅度变化的因素。

3.3 重构数据与定量模型

为了建立质量指标与过程参数之间的定量关系模型，采用傅里叶逆变换对所有参数和指标进行了重构计算，对原始数据中心缺失的数据进行了补充并得到了时间上一一对应的过程参数和质量指标数据。在重构计算中，整个时间跨度(6年)划分为1000个等间隔的时间点，利用公式(2)计算每个时间点的各参数和指标的数值。图3显示了重构计算的结果。

通过图3与图1的比较可以发现，数据随时间的变化在基本轮廓上保持了一致，说明重构数据保持了原始数据的基本信息。但仔细比较各曲线的细节可以进一步发现，无论是采样密度很高的4个参数(x1、x2、x3、x4)还是采样密度较低的参数(x5和y)均得到了平滑处理，既对高密度数据中的快速变动进行了平滑， 也对低密度数据中由于采用时间间隔不合适带来的大幅变动进行了修正，在一定程度上增加了数据的可用性。同时，重构数据对原始数据中的缺失数据进行了有效补充， 因此，数据的重构达到了提升数据质量的目的。更为重要的是，高密度数据的数据点数得到了缩减，而低密度数据的数据点数得到了提高，并且在时间点上一一对应，为建立质量指标和过程参数之间的定量模型提供了可行的数据集。

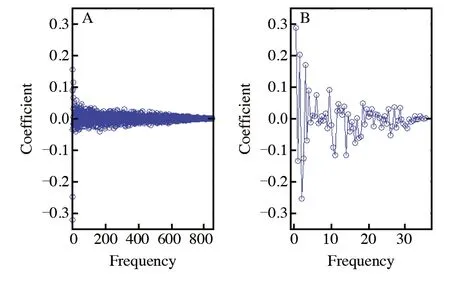
图2 过程参数x1(A)和质量指标y1(B)的傅里叶变换系数Fig.2 Coefficients obtained by Fourier transform of production for parameter x1 (A) and quality for parameter y1 (B), respectively

图3 过程参数(A)和质量指标(B)的重构数据Fig.3 Reconstructed data for production for parameter x1 (A) and quality for parameter y1 (B)

表1是基于重构数据所建立的定量模型及模型的评价参数。建模采用了基于多元线性回归的逐步回归方法，通过对每个自变量参数在回归模型中的显著性进行了删除。表中模型系数为0的参数是指由于置信度大于0.05而被逐步回归移除的参数，在定量模型中没有被使用。另外，由于所有参数和指标均经过了标准化处理， 模型的常数项基本为零(实际计算值均在10-4级别)，因此表中没有列出。RMSE是模型的拟合总误差，即每个质量指标数据拟合误差平方和的均值，数值越小, 表示模型的质量越高。表中的最后一列是模型自预测结果的平均偏差和最大偏差。可以看出，平均偏差均<5%，结合表中的标准偏差数据可以进一步说明, 大部分预测结果的偏差都在可接受的范围之内。因此，所建立的模型具有较好的预测准确性。最大误差的最大值达到17%，说明还存在个别预测误差较大的预测结果，但对实际生产数据来说，此结果仍在可接受的范围。

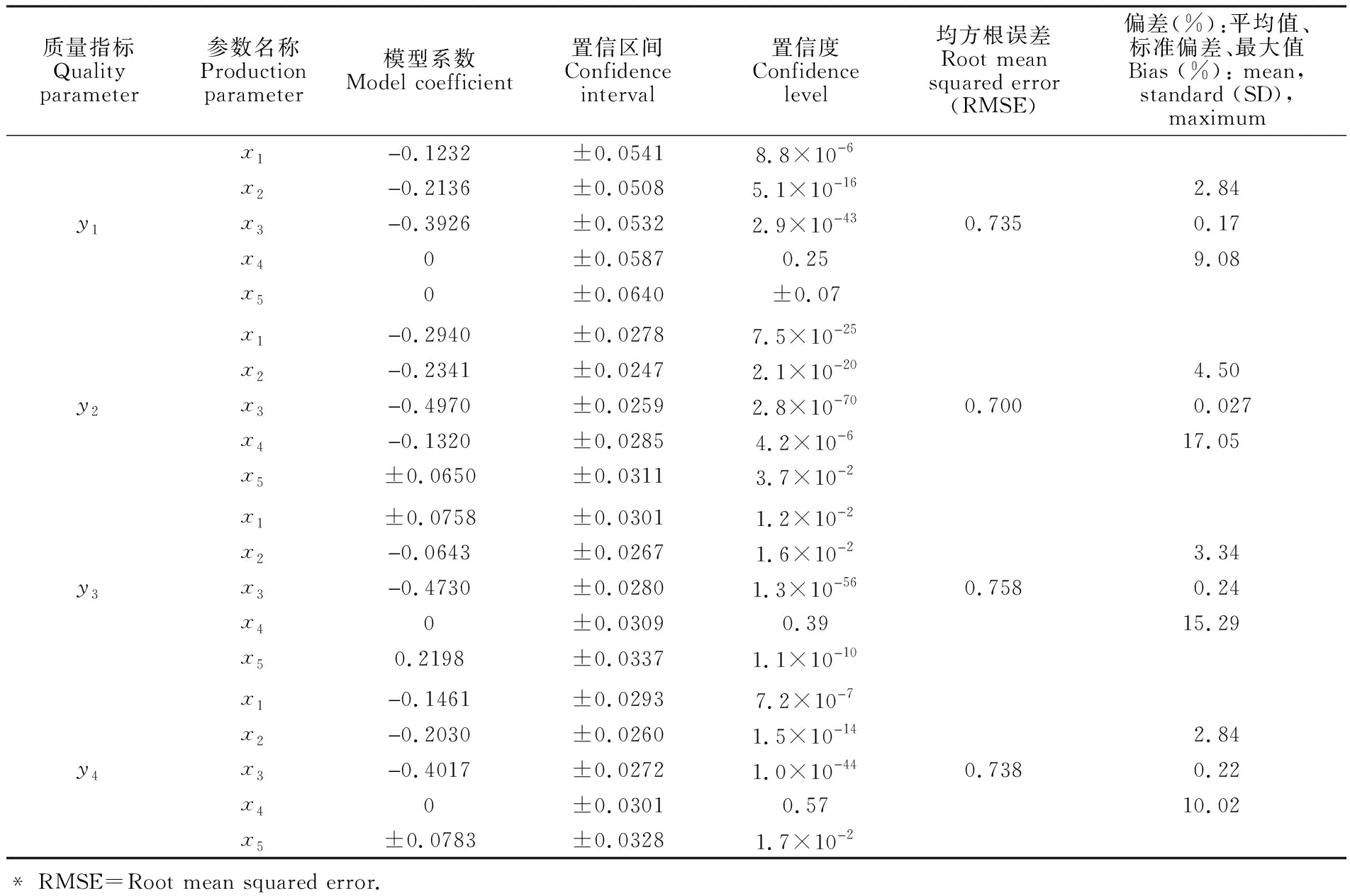
表1 质量指标与过程参数之间的定量关系模型及评价参数

4 结 论

工业生产数据往往具有采样不连续、数据密度差异较大、数据缺失或不完整等特点。本研究针对工业生产数据的特点，采用傅里叶变换对数据进行预处理，实现了数据的平滑、缺失数据的补充以及时间上不能对应等问题，实现了时间上不能一一对应的因变量和自变量之间的模型建立。采用时间跨度为6年的产品质量指标、物理指标和原材料的性能指标等数据，研究了工业生产数据的数据分布，进行了数据变动的周期性分析，建立了产品质量指标与物理指标和原材料性能之间的定量模型，本研究所建立的模型具有较好的预测能力。随着各行业的发展和分析能力的提高，为实际生产服务的大数据分析需求会逐步提升，发展针对分析测试大数据的分析方法具有重要意义。所建立的方法为非连续采样的多参数数据分析提供了一种可行的方法，为工业生产数据，特别是工业生产大数据的数据分析与建模将具有一定的参考价值。