对于停车场区域优化模型研究
翟庭钰 曾钰洁 王森正


摘 要:通过对两种典型停车场设计区域研究,得到家用汽车大小与停车位排放倾斜角度与道路宽度之间的关系,通过Lingo软件对所建立模型进行求解,进而得到停车场车位最佳摆放设计。
关键词:Lingo;动态规划;“单元法”区域划分
随着家用小轿车数量越来越多,与小轿车数量增多相对应的,就是停车场地法日益减少,各大城市“寸土寸金”的情况日益严重,随之而来的“停车”逐渐成为我国各城市普遍面临问题之一。如何综合考虑各方面因素设计停车场的停车位,使之能够获得较大的停车能力,成为了我们国家发展的不可避免的难题。
为解决停车场区域使用效率低下问题,其从标准矩形停车区域面积规划与三角形区域停车位设计方式进行分析与研究,利用单元法区域划分以及非线性规划等方案建立数学模型,对示例区域进行实证分析,并求解出最优停车位规划方案。
1 单通道矩形停车位设计
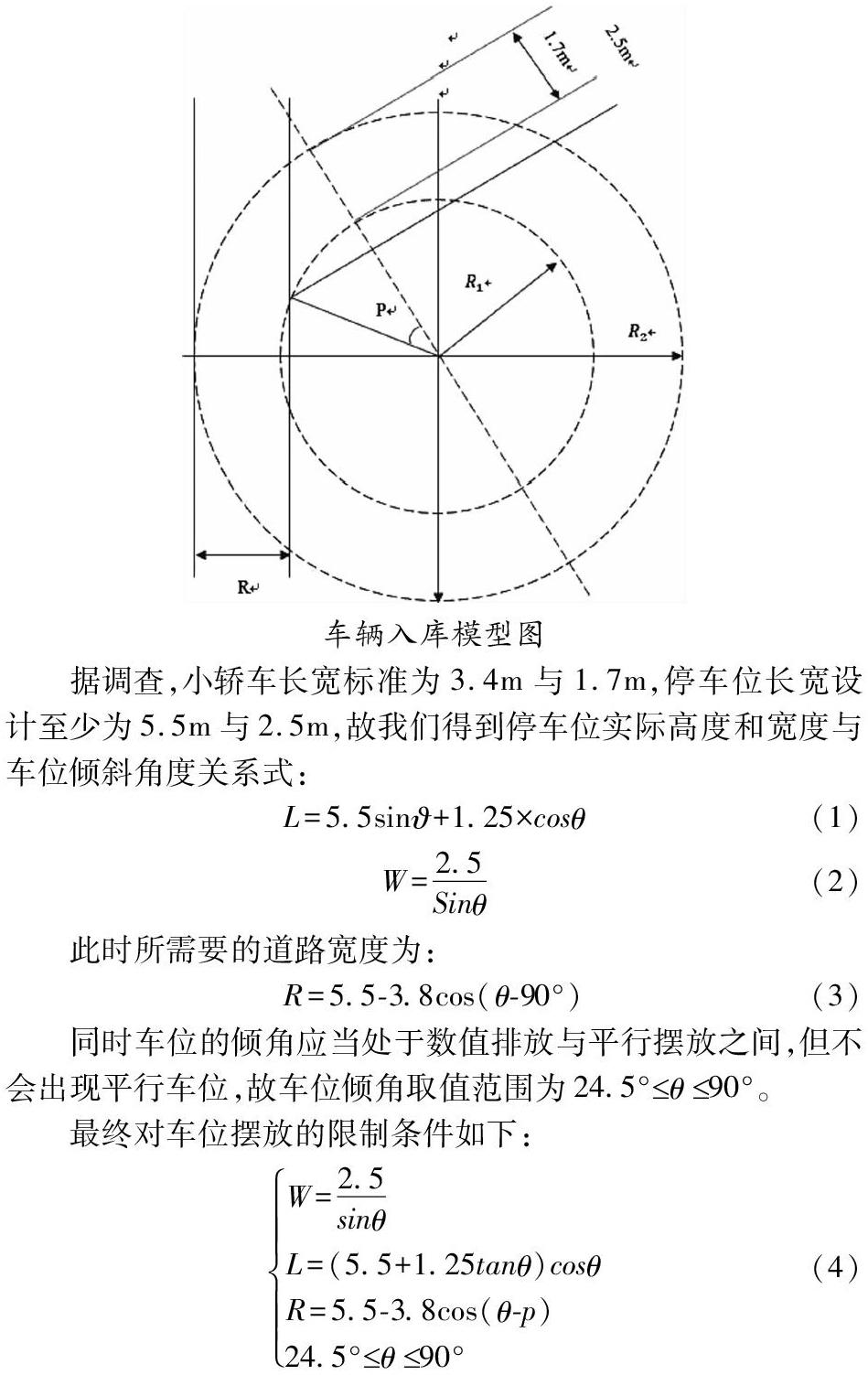
据调查,小轿车长宽标准为3.4m与1.7m,停车位长宽设计至少为5.5m与2.5m,故我们得到停车位实际高度和宽度与车位倾斜角度关系式:
此时所需要的道路宽度为:
我们利用上述限制条件对此区域当中的停车位数量进行求解,每一排的车位都应当与道路相连接,而道路的面积与停车位的总面积之和是不变的,即道路越多,停车位越少。所以我们尽可能要减少道路的数量来增加停车位的数量。
在长为79m,宽为26.5m的标准矩形停车位的场景下,利用Lingo对模型求解,我们计算出各项参数最优取值为:
故容纳车位最多的方案为4排停车位2条道路。即每个停车位的高度为5.33m,宽度为2.95m,倾斜角度为1.01弧度,约为64.2°,所需要的道路的宽度为1.93m。
可以看出,利用动态规划模型所计算出的最优规划方案并不为常见情况下的竖直摆放。在停车位倾斜1.01弧度下不仅使得车位数量摆放最多,同时也方便于车主停车,有利于停车场车辆流通效率。
2 其他矩形区域车位摆放
但区域长度为250m,宽度为43m,同时出入口方向为南北方向,所以我们在规划停车位的时候,井停车位当中的通道也设置为南北方向才能使的停车位个数最多。我们通过区域的宽度估算,其大致能规划6排停车位3列道路,我们将长宽限制条件带入到代码中求解,得到的结果如下表所示。
可以得出在此區域当中的车位规划为垂直车位,每排车位为100个,总共能容纳600个,属于生活当中的常规设计。
3 结语
本文通过对面积的停车场设计区域规划布局进行研究,提出了车位倾斜度与摆放个数动态规划模型,通过计算最优车位摆放个数得出如下如下结论:
(1)一般而言,车位的布置方案是需要根据实际场地具体情况进行设立,有些时候,标准平行摆放车位能够达到最好的区域利用率,但是还有一些情况下倾斜车位效果更好,兼顾利用率以及车主使用感受。
(2)在分析设计停车位安排的过程中,我们建立的局部优化模型可以很好的解决由小问题组成的大问题,在很多方面,诸如房屋的安排等等均可以采用局部优化模型。另外,我们探究的停车位设计问题所采用的方法,还可以广泛运用于其他设计中,例如小区设计等等,都能够起到很好的举一反三作用。
参考文献:
[1]高新涛,陈丽.停车场中停车位排布方式优化设计[J].河南科技,2014(20):149-150.
[2]仲子平,闫瑜.汽车文化[M].北京航空航天大学出版社,2012(第2版).
[3]过秀成.城市停车场规划与设计[M].中国铁道出版社,2008.
作者简介:翟庭钰(1999-),男,汉族,重庆人,本科,研究方向:物流管理。

