多阶段投资组合的动态规划模型

夏贞丽

【摘要】动态规划所研究的对象是多阶段决策问题， 它的目的就是利用动态规划原理建立投资决策问题的一类数学模型， 来寻求一个策略， 使得每个阶段的效益总和达到最优. 本文给出了数学模型的求解方法并利用实例验证了算法的有效性.

【关键词】数学模型 动态规划 多阶段投资决策

一. 引言

多阶段决策问题是投资者在连续的几个投资阶段中每个阶段里都进行投资， 其目的是使得到最后一个投资阶段结束时， 投资者进行多次投资的收益总和尽可能大， 这些投资阶段之间是相互关联的， 面对众多的投资项目， 如何合理的安排资金成为决策部门关心的焦点， 而动态规划方法的关键在于正确写出基本递推关系式， 首先将问题的过程分成几个相互联系的阶段， 恰当的选取状态变量和决策变量及定义最优值函数， 从而把一个大问题化成一族同类型的子问题， 然后逐个求解， 即从边界条件开始， 逐阶段递推求优， 在每个子问题求解过程中均利用了它前面的子问题的最优结果， 依次进行， 最后一个子问题所得到的最优解就是整个问题的最优解.

二. 动态规划在多阶段投资组合中的应用

1.案列介绍

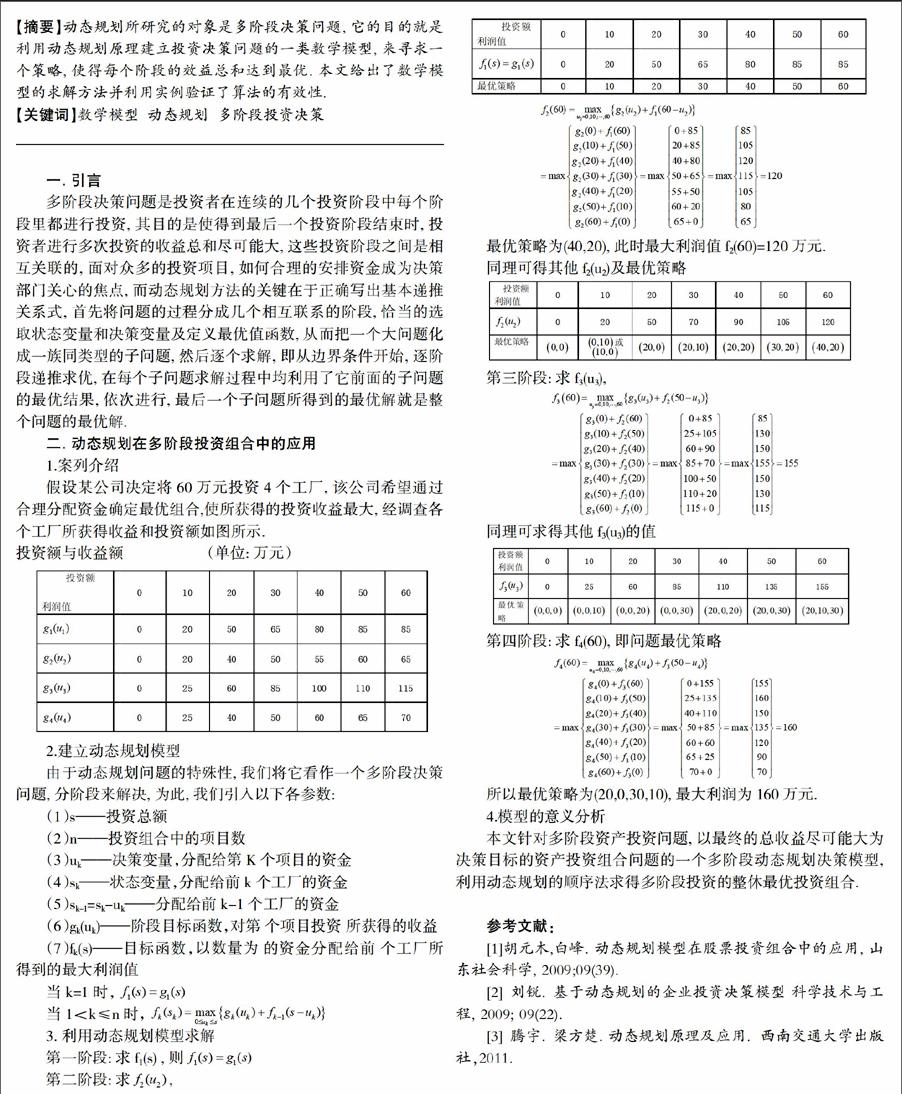
假设某公司决定将60万元投资4个工厂， 该公司希望通过合理分配资金确定最优组合，使所获得的投资收益最大， 经调查各个工厂所获得收益和投资额如图所示.

投资额与收益额 （单位： 万元）

2.建立动态规划模型

由于动态规划问题的特殊性， 我们将它看作一个多阶段决策问题， 分阶段来解决， 为此， 我們引入以下各参数：

（1）s——投资总额

（2）n——投资组合中的项目数

（3）uk——决策变量，分配给第K个项目的资金

（4）sk——状态变量，分配给前k个工厂的资金

（5）sk-1=sk-uk——分配给前k-1个工厂的资金

（6）gk（uk）——阶段目标函数，对第 个项目投资 所获得的收益

（7）fk（s）——目标函数，以数量为 的资金分配给前 个工厂所得到的最大利润值

当k=1时，

当1

3. 利用动态规划模型求解

第一阶段： 求f1（s） ， 则

第二阶段： 求 ，

最优策略为（40，20）， 此时最大利润值f2（60）=120万元.

同理可得其他f2（u2）及最优策略

第三阶段： 求f3（u3），

同理可求得其他f3（u3）的值

第四阶段： 求f4（60）， 即问题最优策略

所以最优策略为（20，0，30，10）， 最大利润为160万元.

4.模型的意义分析

本文针对多阶段资产投资问题， 以最终的总收益尽可能大为决策目标的资产投资组合问题的一个多阶段动态规划决策模型， 利用动态规划的顺序法求得多阶段投资的整休最优投资组合.

参考文献：

[1]胡元木，白峰. 动态规划模型在股票投资组合中的应用， 山东社会科学， 2009；09（39）.

[2]刘锐.基于动态规划的企业投资决策模型 科学技术与工程， 2009； 09（22）.

[3]腾宇.梁方楚. 动态规划原理及应用. 西南交通大学出版社，2011.