由一道错解题引出的对机械效率高低的讨论

李学武

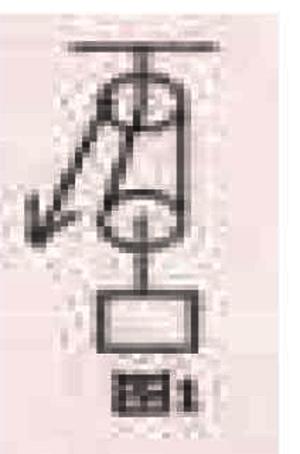
在教学机械效率时，有少数学生有轻敌思想，总认为这一节比较容易，其实不然。特别是部分计算题，难度是比较大的。概念、公式、以及有关的物理量也比较复杂，学生们总是难以把握，而机械效率的高低就更加复杂，难以理解了。在解答下面这道看是简单的习题时就出现了错误。

例1：某大理石的密度为2.5×10³Kg/m³，体积为0.016m³（g=10N/kg）

⑴若工人用如图1所示的滑轮组来提升此大理石，用250N的力恰好能将大理石竖直向上匀速提升，则该滑轮组此时的机械效率为多少？（不计绳重和摩擦）

⑵若用此滑轮组将重为900N的另一物体竖直向上匀速提升1.5m，则拉力在这一过程中所做的功是多少？

错解：①该滑轮组的机械效率为：

η=w_有/w_总=Gh/Fs=mgh/Fs=ρgvh/Fs

=（2.5×10³Kg/m³×10N/kg×0.016m³×h）/（250N×2h）=80%

②拉力做的总功，根据η=w_有/w_总可得，

w_总=w_有/η=（900N×1.5m）/80%=1687.5j

作为教者，显然易见，第一小题是正确的，问题就出在第二小题上，学生在解答时，盲目地套用了第一小题的计算结果，究其原因就是学生对影响机械效率高低的因素认识不够。以为在这两道小题中的机械效率是固定不变的，其实不然。那么是什么因素影响了滑轮组机械效率的高低呢？我们不妨来看看下面的两道与机械效率有关的习题，便可管中窥豹，略见一斑。

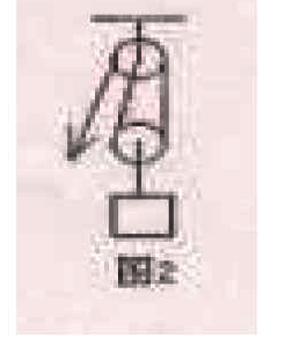
例2：如图2，每个滑轮重10N，用这个滑轮组分别把50N和70N的重物匀速提升到2m的高度分别求出他们工作时的机械效率η₁和η₂（不计绳重和摩擦）

解：根据机械效率的定义：

①当提起50N的重物时：

η₁=（50N×2m）/[（50+10）N×2m]

=83.3%

②当提起70N的重物时;

η₂=（70N×2m）/[（70+10）N×2m]

=87.5%

例3：如图3甲和乙的滑轮组每个滑轮重10N，分别用他们将60N的重物匀速提升到2m的高度，试分别求出他们工作时的机械效率η₁和η₂（不计绳重和摩擦）

解：①如图3甲，该滑轮组的机械效率为：

η₁=（60N×2m）/[（60+10）N×2m]

=85.7%

②如图3乙，该滑轮组的机械效率为：

η₂=（60N×2m）/[（60+10+10）N×2m]

=75%

我们从例2和例3不难看出：在不计绳重和摩擦的情况下，使用同一滑轮组提升不同的重物，物体越重，滑轮组的机械效率越高;用不同的滑轮组提升相同的重物，动滑轮越轻，机械效率越高。由此可知：在不计绳重和摩擦的情况下，所拉物重和轮重是影响滑轮组机械效率高低的因素。

通过分析，我们再回过头来看一看例1的正確解答：

根据第一小题的情况，用同一滑轮组提升不同的重物，其机械效率是不同的。因而应先求出滑轮的重力。根据受力分析，滑轮和物体一起受平衡力作用：

2F=G_轮+G_物

G_轮=2F-G_物=2×250N—400N=100N

则拉力所做的功（即总功）=（900+100）N×1.5m=1500j