合情推理与演绎推理相辅相成

林水助

在实施新课改之前，我国传统数学教育重视演绎推理，而在实施新课改后，演绎推理相对来说被弱化，与之相比，合情推理得到重视。一线的中小学教师，还有一些高校学者都积极投入到对“合情推理”的研究当中去，试图在教学活动中引入合情推理，为的是契合课标的要求，而演绎推理在数学上是作为一种严格的推理方法使用，是数学严谨性的体现。 因此，合情推理与演绎推理是相辅相成的。

笔者以具体案例加以阐述，以执教新北师大版六年级下册第一单元复习中一实践活动为例，本课教材中，设计了一个用4张完全一样的长方形纸（长16cm，宽4cm）卷成不同的圆柱形的活动，其实践活动目的是通过 “用长方形纸卷圆柱形”的探索活动，鼓励学生应用所学的圆柱的表面积和体积的知识，经历探索规律的过程，体会一些变量之间的关系。教学重难点：体会在圆柱侧面积相等的情况下，体积不等，理解其原由。

一、运用合情推理，发现规律

《数学课程标准》中指出：“推理能力的发展应贯穿在整个数学学习过程中。推理是数学的基本思维方式，也是人学习和生活经常使用的思维方式。在小学阶段，主要学习合情推理，即归纳推理和类比推理。而归纳推理又多表现为不完全归纳推理”。在本课教学中，先采用合情推理中的不完全归纳法推理，让学生经过观察、猜想、实验、比较，再进行归纳、类比，验证得出规律。

教学实例简述：

1、观察和猜想

教师拿出两张同样的长方形纸，一张横着卷成圆柱形，另一张竖着卷成圆柱形，两个圆柱的体积一样大吗？学生出现不同的意见：两个圆柱的体积一样大，两个圆柱的体积不一样大，认为粗短的圆柱体积大，或觉得细长的圆柱体积大。

2、实验和比较

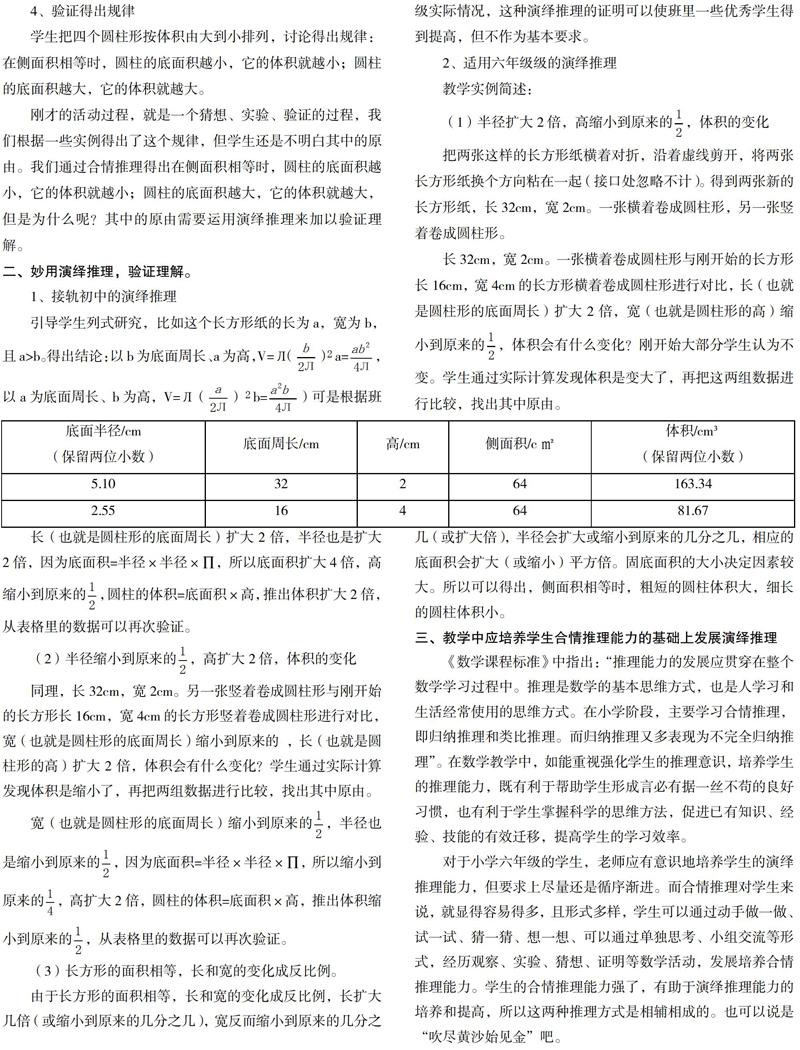
学生小组合作完成验证活动，将纸围成不同的圆柱，把测量和计算的数据填在下面的表格中。

学生得出结论：侧面积相等时，粗短的圆柱体积大，细长的圆柱体积小。

3、归纳和类比

把两张这样的长方形纸横着对折，沿着虚线剪开，将两张长方形纸换个方向粘在一起（接口处忽略不计）。得到两张新的长方形纸，长32cm，宽2cm。一张横着卷成圆柱形，另一张竖着卷成圆柱形。把测量和计算的数据填在表格中。

4、验证得出规律

学生把四个圆柱形按体积由大到小排列，讨论得出规律：在侧面积相等时，圆柱的底面积越小，它的体积就越小;圆柱的底面积越大，它的体积就越大。

刚才的活动过程，就是一个猜想、实验、验证的过程，我们根据一些实例得出了这个规律，但学生还是不明白其中的原由。我们通过合情推理得出在侧面积相等时，圆柱的底面积越小，它的体积就越小;圆柱的底面积越大，它的体积就越大，但是为什么呢？其中的原由需要运用演绎推理来加以验证理解。

二、妙用演绎推理，验证理解。

1、接轨初中的演绎推理

引导学生列式研究，比如这个长方形纸的长为a，宽为b，且a>b。得出结论：以b为底面周长、a为高，V=Л（ ） a= ，以a为底面周长、b为高，V=Л（ ） b= ）可是根据班级实际情况，这种演绎推理的证明可以使班里一些优秀学生得到提高，但不作为基本要求。

2、适用六年级级的演绎推理

教学实例简述：

（1）半径扩大2倍，高缩小到原来的 ，体积的变化

把两张这样的长方形纸横着对折，沿着虚线剪开，將两张长方形纸换个方向粘在一起（接口处忽略不计）。得到两张新的长方形纸，长32cm，宽2cm。一张横着卷成圆柱形，另一张竖着卷成圆柱形。

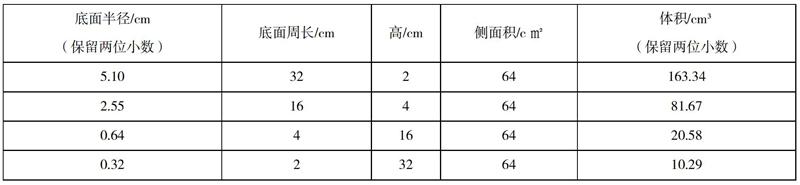
长32cm，宽2cm。一张横着卷成圆柱形与刚开始的长方形长16cm，宽4cm的长方形横着卷成圆柱形进行对比，长（也就是圆柱形的底面周长）扩大2倍，宽（也就是圆柱形的高）缩小到原来的 ，体积会有什么变化？刚开始大部分学生认为不变。学生通过实际计算发现体积是变大了，再把这两组数据进行比较，找出其中原由。

长（也就是圆柱形的底面周长）扩大2倍，半径也是扩大2倍，因为底面积=半径×半径×∏，所以底面积扩大4倍，高缩小到原来的 ，圆柱的体积=底面积×高，推出体积扩大2倍，从表格里的数据可以再次验证。

（2）半径缩小到原来的 ，高扩大2倍，体积的变化

同理，长32cm，宽2cm。另一张竖着卷成圆柱形与刚开始的长方形长16cm，宽4cm的长方形竖着卷成圆柱形进行对比，宽（也就是圆柱形的底面周长）缩小到原来的 ，长（也就是圆柱形的高）扩大2倍，体积会有什么变化？学生通过实际计算发现体积是缩小了，再把两组数据进行比较，找出其中原由。

宽（也就是圆柱形的底面周长）缩小到原来的 ，半径也是缩小到原来的 ，因为底面积=半径×半径×∏，所以缩小到原来的 ，高扩大2倍，圆柱的体积=底面积×高，推出体积缩小到原来的 ，从表格里的数据可以再次验证。

（3）长方形的面积相等，长和宽的变化成反比例。

由于长方形的面积相等，长和宽的变化成反比例，长扩大几倍（或缩小到原来的几分之几），宽反而缩小到原来的几分之几（或扩大倍），半径会扩大或缩小到原来的几分之几，相应的底面积会扩大（或缩小）平方倍。固底面积的大小决定因素较大。所以可以得出，侧面积相等时，粗短的圆柱体积大，细长的圆柱体积小。

三、教学中应培养学生合情推理能力的基础上发展演绎推理

《数学课程标准》中指出：“推理能力的发展应贯穿在整个数学学习过程中。推理是数学的基本思维方式，也是人学习和生活经常使用的思维方式。在小学阶段，主要学习合情推理，即归纳推理和类比推理。而归纳推理又多表现为不完全归纳推理”。在数学教学中，如能重视强化学生的推理意识，培养学生的推理能力，既有利于帮助学生形成言必有据一丝不苟的良好习惯，也有利于学生掌握科学的思维方法，促进已有知识、经验、技能的有效迁移，提高学生的学习效率。

对于小学六年级的学生，老师应有意识地培养学生的演绎推理能力，但要求上尽量还是循序渐进。而合情推理对学生来说，就显得容易得多，且形式多样，学生可以通过动手做一做、试一试、猜一猜、想一想、可以通过单独思考、小组交流等形式，经历观察、实验、猜想、证明等数学活动，发展培养合情推理能力。学生的合情推理能力强了，有助于演绎推理能力的培养和提高，所以这两种推理方式是相辅相成的。也可以说是“吹尽黄沙始见金”吧。