例说数学建模 抓牢知识应用
何先

【摘要】数学教育不仅要教给学生数学知识,更要教给学生运用所学知识去解决实际问题。教师要善于在教学中把数学的概念法则和解题方法进行模型化,使学生既能掌握数学的基础知识,又能应用数学知识解决生活和生产中出现的问题。这种应用知识从实际问题中抽象、提炼出数学模型的过程就称为数学建模。应用数学解决实际问题,这就是学习数学的真正目的所在。教学中,务必抓牢抓实。
【关键词】建模 抓牢 应用
【中图分类号】G633.6
【文献标识码】A
【文章编号】1992-7711(2020)20-099-02
在百科中是这样描述数学建模的:数学建模(Mathematical Modeling)是利用数学工具解决实际问题的重要手段。数学教育不仅要教给学生数学知识,更要教给学生运用所学知识去解决实际问题。教师要善于在教学中把数学的概念法则和解题方法进行模型化,使学生既能掌握数学的基础知识,又能应用数学知识解决生活和生产中出现的问题。当需要从定量的角度分析和研究一个实际问题时,人们就要在深入调查研究、了解对象信息、作出简化假设、分析内在规律等工作的基础上,用数学的符号和语言,把它表述为数学式子,也就是数学模型(Mathematical Model),然后用通过计算得到的模型结果来解释实际问题,并接受实际的检验。这种应用知识从实际问题中抽象、提炼出数学模型的过程就称为数学建模。
数学模型是一种模拟,是用数学符号、数学式子、程序、图形等对实际问题本质属性的抽象而又簡洁的刻划。数学模型一般并非现实问题的直接翻版,它的建立常常既需要人们对现实问题深入细微的观察和分析,又需要人们灵活巧妙地利用各种数学知识。它和真实的事物有着本质的区别。那通过怎样的流程,能够将实际问题与数学模型有机地融合在一块呢?以下利用数学中的直线对称模型来解决生活中的一类实际问题。
【问题情景】在一条河道(近似直线)的一边有A、B两个村庄,设A、B到河道的垂直处分别为C、D,经测量AC=2km,BD=3km,CD=4km,现欲在河道边建造一个小型自来水厂,给A、B两村提供生活用水,问自来水厂建在什么位置,使铺设到A、B两村所用水管的总长最节省?铺设水管的总长最小值是多少?
【模型假设】本题是一个实际生活中的应用问题,把它放在数学中,设自来水厂建造位置为M,实际上就是求AM+BM的最小值(如图)。如何求最小值呢?因为AMB是一条折线,我们能不能把这三个点拉到同一条直线上来呢?这就需要利用数学中的对称方法来实现了。下面我们先来看看,数学中是怎样求一个点关于一条直线的对称点坐标的?
【模型准备】一个点关于一条直线的对称点坐标的求法:
设点P(x0,y0)关于直线l:Ax+By+c=0的对称点为Q(x',y'),那怎样来求x',y'的值呢?在解析几何中是从以下两个方面着手考虑的:
【模型建立】在前面的问题中,问自来水厂建在什么位置,使铺设到A、B两村所用水管的总长最节省(如图)。下面我们一起来利用数学中的关于直线对称问题的模型进行探索:
首先作点A关于直线CD的对称点A',根据对称性质有AM=A'M,所以AM+BM=A'M+BM,故只需求出A'M+BM的最小值。根据两点之间线段最短,此时连接A'B,与直线CD的交点M, 就是自来水厂建造的位置。
【模型求解】以CD所在直线为x轴,CD的中点O为坐标原点建立直角坐标系(如图),依题意得,A(-2, 2),B(2, 3),作点A关于x轴的对称点A',则A'(-2, -2)。
根据对称性质,有AM=A'M,∴AM+BM=A'M+BM,故只需求出A'M+BM的最小值。根据两点之间线段最短,此时连接A'B,与直线CD的交点M,可使A'M+BM取最小值,所以点M就是自来水厂建造的位置。
而线段A'B的长度就是自来水厂到A、B两村铺设水管总长的最小值。
即AM+BM的最小值是6.4km。因此,自来水厂应建在CD之间,离D点距离是2.4km处,而自来水厂到A、B两村铺设水管总长的最小值是6.4km.
【模型分析】此问题中,看似求距离之和最小,实则通过分析我们发现,它实际上可以转化为数学中的对称问题和两点间的距离问题加以解决,这样就建立了关于直线对称问题的数学模型,实现了将实际生活中的问题转化为数学问题这一跨越,完成了数学建模这一高级进程,这在培养学生的数学应用能力方面,又迈上了一个新台阶,是一个非常重要的突破。
【模型验证】为什么自来水厂建在A'B与直线CD的交点处M时,才能使自来水厂到A、B两村铺设水管的总长最节省呢?我们不妨在CD之间任取一点M'(异于图中的点M), 这时我们只需比较AM+BM与AM'+BM'的大小。根据对称性质有:AM'=A'M',所以AM'+BM'=A'M'+BM',
因为AM+BM=A'B,所以,转换为比较A'B与A'M'+BM'的大小。
显然,在△A'BM'中,有A'M'+BM'>A'B。所以,自来水厂只有建在A'B与直线CD的交点处M时,自来水厂到A、B两村铺设水管的总长最节省。
这就充分验证我们求出的结果与现实生活中的处理方法是相符的,是完全合理的。
【模型应用】从上面实例我们知道,利用直线对称的模型,解决了生活中关于距离之和的最小值问题,现在我们进一步运用这个模型,来解决生活中的类型问题。
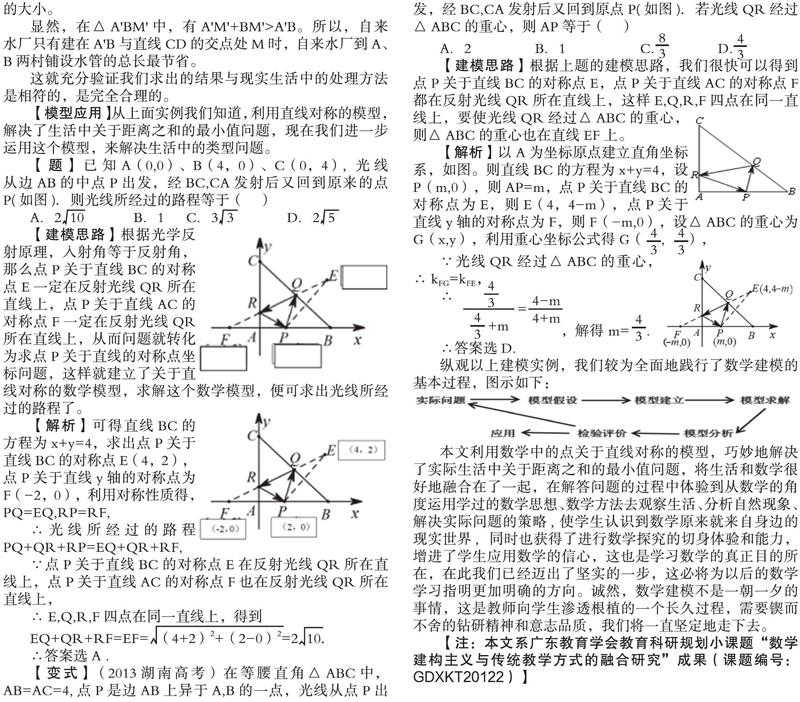
【题】已知A(0,0)、B(4,0)、C(0,4), 光线从边AB的中点P出发,经BC,CA发射后又回到原来的点P(如图).则光线所经过的路程等于( )
A.2 10 B.1 C.3 3 D.2 5

