协同粒子群算法下的火工品参数辨识
毕雪芹 李蓓蕾 徐文文

【摘 要】为解决火工品起爆过程中线性函数不能解决的不确定性、非线性强和火工品参数难获得的问题,文章采用Volterra模型与协同粒子群算法相结合的思想对火工品参数进行获取,从而对火工品进行合理分析,确保火工品的安全性和可靠性。通过对协同粒子群算法、递推最小二乘法的实验仿真结果进行对比可以看出,文章基于协同粒子群算法(CPSO)的Volterra模型参数辨识算法,对标准粒子群算法的过早收敛问题、遗传算法搜索速度慢的问题进行了有效的改善,对算法的辨识速度和辨识精度有很大的提升。
【关键词】火工品;Volterra级数;协同粒子群算法
【中图分类号】TJ45 【文献标识码】A 【文章编号】1674-0688(2020)09-0097-03
0 引言
火工品作为一次性使用的装置,其内部装有火药或炸药。当火工品受到外界刺激与干扰的情况下,其内部的火药或炸药会燃烧或爆炸,从而火工品输出能量完成工作。作为先进军事武器系统的第一能源产品,火工品的安全性和可靠性是人们关注的重点。火工品参数可以表征火工品性能,但火工品对环境参数非常敏感,这使得火工品参数的获取变得更加困难,测量准确性变差。我国对火工品参数研究的公开文献也较少,张莉莉为了测试火工品参数,研究了一种火工品测试系统,通过实验,对火工品的火回路电流、桥路阻值、桥丝熔断时间进行实验,验证系统的有效性和可行性[1]。严楠等人根据火工品的输出压力、速度、加速度、位移、推力、温度等信号特征及量程,提出一套可供选择的动态多参数测试系统[2]。强涛等人提出把无损检测技术和BP神经网络模型相结合,对火工品的安全电流进行预测,实验结果证实了方法的可行性[3]。现存的火工品测试方法在一定程度上促进了火工品的研究,但随着人们要求的提高,提出新的研究方法是不可避免的。协同粒子群算法是在标准粒子群优化算法基础上的改进,它克服了智能算法的弊端,此算法收敛快、辨识精度高、辨识容易,因而在研究中被广泛应用,在实际问题的解决中也凸显优势。于雷将协同算法应用于航空发动机多管道布局中,并利用MATLAB进行仿真,用结果验证算法的可行性,为多管道布局提供了新思路[4]。吕微微等人将协同粒子群算法应用到系统辨识中,通过仿真验证了此方法在系统辨识方面的有效性,为后续系统辨识提供基础[5]。
本文将Volterra级数模型和协同粒子群算法结合起来,推出一种新的火工品参数辨识研究方法,为后期的火工品研究和分析等提供理论支持。
1 火工品起爆模型
火工品起爆过程中存在严重的非线性,使得火工品起爆参数的理论结果与实际结果存在严重的误差。Volterra级数模型通过系统的输入和输出确定,而与输入和输出的状态无关,采用Volterra级数描述火工品起爆过程,可以完全通过Volterra级数的时域核和频域核确定火工品起爆的内在特性,从而得到火工品参数。
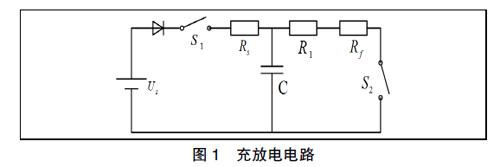
电火工品的充电式点火电路模型如图1所示,图1中包括充电电路和对火工品的放电电路。其中,Us为电源,即充电电路中的给定电压;Rs为充电电阻,充电电路中的二极管防止电流倒流;R1为放电电路中限流电阻,防止电路中电流过大;Rf为电起爆器电阻;C为电容,为火工品放电实现火工品的起爆;S1、S2分别为充电电路与放电电路的控制开关。
由KVL、KCL得到下列表达式:
电容充电时:
上式中,Uc为电容端电压,ts为充电时间,Wc为电容充电储存的能量。
电容放电时:
进行Z变换并离散化后整理得:
输出为电流,输入为电压,待辨识参数为a1,a2,a3;根据式(2),得到R1,Rf,C。
2 算法仿真验证
2.1 协同粒子群算法
协同进化算法所具有的特点即为多个种群并行搜索。在每次迭代过程中,采用不同的进化机制,既有利于扩展对全局的搜索,也有助于在搜索后期对最优值的快速收敛[6]。
协同粒子群算法的基本思路如图2所示。
2.2 算例验证
作为辨识目标的Volterra模型如式(7)所示:
从表达式中可以看出,模型的核向量为H=[2.71,-0.55,0.81,1.06,0,0,1.61,-1.75,0]T。利用本文提出的协同粒子群算法对上述Volterra模型进行辨识,设置系统的输入信号为[0,1]之间的均匀白噪声信号,种群大小为80,空间维数设定为20,最大迭代次数为600,然后进行多次辨识测试实验,然后取平均值。
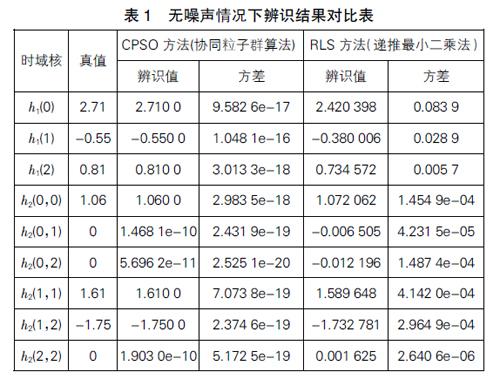
表1和表2分别为协同粒子群算法、递推最小二乘法(RLS)无噪声条件下和噪声比为20 dB情况下所得到的Volterra模型参数的估计值。
图3和图4分别是无噪声条件和噪声比在20 dB下Volterra级数核函数h2(1,2)的收敛曲线。
在无噪声情况下,协同粒子群算法和最小递推二乘法都能较好地与真实值吻合,但协同粒子群算法的辨识结果的平均值更接近于真实值,可以证明协同粒子群算法辨识精度较高。在有噪声条件下,协同粒子群算法和递推最小二乘法都受到了一定的影响,但是CPSO算法能在一定的迭代步数能很快收敛于真值,RLS算法在收敛的过程中也能收敛于真值,但收敛过程中并不稳定。
3 实验验证
通过上述算法仿真协同粒子群算法的有效性得到验证,我们把协同粒子群算法应用到火工品起爆模型中,对模型中的参数进行辨识,设置迭代步数为1 000,得到模型参数,然后利用模型参数与火工品参数的关系得到相关火工品参数。图5和图6是火工品参数的辨识曲线。
4 结论
本文针对火工品参数的辨识,提出基于协同策略的粒子群优化算法,利用Volterra级数模型建立火工品起爆模型,克服了火工品起爆过程中的非线性。研究发现,与其他算法相比,协同粒子群优化算法可以获得较好的参数识别精度。本文提出的算法为非线性系统Volterra模型辨识提供了一种新的有效方法,对后续的非线性系统研究奠定理论基础。
参 考 文 献
[1]张莉莉,吴永红,张月魁,等.火工品电参数测试技术研究[J].宇航计测技术,2018,38(6):87-90,95.
[2]严楠,付永杰.火工品输出动态多参数测试系统的构建与考虑[J].宇航计测技术,2008,28(2):28-32.
[3]强涛,周彬,秦志春,等.桥丝式电火工品安全电流的预测[J].南京理工大学学报(自然科学版),2006,30(1):110-112.
[4]于雷.基于协同进化粒子群算法的航空发动机多管路布局优化[J].电子工程,2020,28(2):17-21.
[5]吕微微,張宏立.基于协同进化粒子群算法的系统辨识[J].计算机仿真,2016,33(1):336-339.
[6]俞欢军,张丽平,陈德钊,等.基于反馈策略的自适应粒子群优化算法[J].浙江大学学报(自然科学版),2005,
39(9):1286-1291.
[7]程善美,张益.基于协同粒子群算法的PMSM在线参数辨识[J].电气传动,2012,42(11):3-6.
[8]周頔,孙俊,须文波.具有量子行为的协同粒子群优化算法[J].控制与决策,2011,26(4):582-585.
[9]赵静芳.火工品多参数测试系统设计[D].太原:中北大学,2011.
[10]叶迎新.火工品技术[M].北京:国防工业出版社,2014.
[11]程善美,张益.基于协同粒子群算法的PMSM在线参数辨识[J].电气传动,2012,42(11):3-6.
[12]蒋静,李志农.基于量子粒子群优化的Volterra核辨识及故障诊断方法研究[D].河南:郑州大学,2010.
[13]周立启.基于Volterra级数的非线性模拟电路故障诊断方法的研究[D].西安:西安电子科技大学,2012.
[14]王春暖,李文卿,吴庆朝.基于改进PSO优化模糊神经网络的数控机床故障诊断技术研究[J].机床与液压,2016,44(3):192-197.

