基于进化Kriging模型的金属框板结构优化研究

王迪 刘祎萍 武亮

【摘 要】金属加筋板在飞机结构设计中应用广泛，其优化改型设计亦备受重视，文章将借助试验设计和进化Kriging近似模型对金属加筋板尺寸进行优化设计，并采用多目标遗传算法NSGA-Ⅱ对近似模型寻优得到最优解。通过对金属框板结构稳定性优化计算结果分析，可以确定所提出的优化设计效果显著且优化效率高。

【关键词】尺寸优化;加筋板;屈曲;Kriging模型

【中图分类号】V229 【文献标识码】A 【文章编号】1674-0688（2020）09-0063-04

0 引言

航空结构的稳定性是关系到结构安全性及经济性的重要问题。结构的失稳具有突然性，因此失稳造成的破坏往往后果严重，稳定性问题在结构设计中至关重要。进行结构稳定分析的主要目的之一是求出结构的屈曲临界载荷。结构稳定设计的最终目标，是使设计出来的结构在使用载荷下整个结构体系安全可靠，不发生失稳。筋条能大大提高加筋板结构的承载能力，因而比光板具有更好的承载性能。加筋板结构失效模式众多[1]，对其进行优化设计具有重要的研究价值。加筋板结构中其筋条形式、位置及尺寸互为变量，相互影响，使其优化模型复杂化，求解过程中难度增大[2]。

目前，各种优化方法被国内外学者应用于金属加筋板结构优化设计研究中，其中朴春雨等人[3]应用计算机技术编程实现优化目标，以理論结合工程实际对“T”形整体加筋板和角型铆接板进行了优化。Rikards等人[4]运用代理模型技术优化加筋板结构，优化效率大大提高。Fatemi等人[5]运用遗传算法求解全局最优解，同时解决离散变量问题。Langer等人[6]以进一步增加加强筋形式为变量，使用有限元进行高精度分析，结合前人经验，既保证精度又提高优化效率。

1 框板结构优化方法

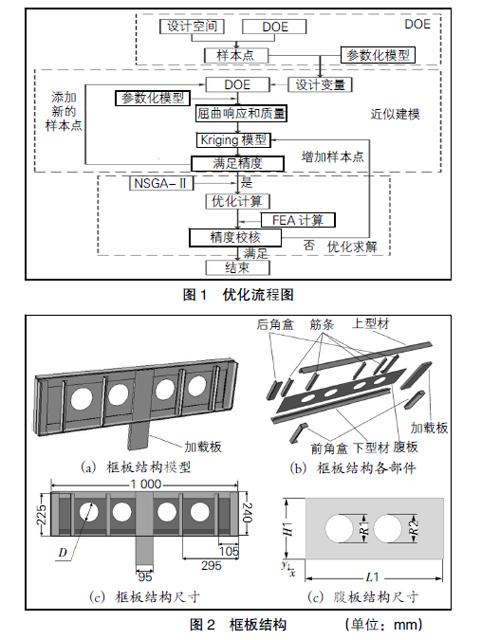
本文对金属框板结构进行尺寸优化设计，设计变量为各个部件的形状尺寸。设计过程的总体思想是利用实验设计方法在设计域内选取样本点集，为获取各个样本点的重量及临界屈曲载荷，使用Abaqus建立参数化有限元模型，并对各个样本点对应的结构有限元模型进行分析，然后利用这些样本点和响应值分别建立重量、屈曲载荷的Kriging近似模型，最后应用遗传算法对多目标优化问题进行求解。

1.1 试验设计方法

试验设计方法是通过控制某些设计参数的变化来研究对设计实验的影响的方法。利用试验设计方法可以合理安排试验方案，其中包括试验所需样本点的采集和样本点在设计域内的分布，寻找影响输出的主要因素，并且研究众多因素之间的相互影响作用大小。该方法在建立近似模型的应用中行之有效，Simpsonr[7]通过大量Kriging模型数据验证了这一点，并且在实验设计中运用拉丁超立方试验设计方法的优秀表现，在实验设计过程中广泛应用。

1.2 进化Kriging模型

Kriging近似模型以变异函数和结构分析为基础，可以实现对区域化变量求最优、线性、无偏内插估计值，是一种基于随机过程的统计预测方法，不依赖于随机误差的存在，具有平滑效应和估计方差最小的统计特征[8]。虽然该模型只是建立在拟合、差值等技术之上，有些情况下并不能完整地反映研究目标的特性，但是它的优势在于可以用有限的样本表示系统的物理实质，所以近似模型精度的验证体系至关重要。本文在优化进行前对近似模型进行精度验证。若满足精度，则计算结束;否则将最优解作为样本点加入样本点集中并加入新的样本点重新建立近似模型，其优化流程图如图1所示。

1.3 多目标优化问题

本文的优化目标为最小重量和最大屈曲因子。针对多目标优化问题，本文的优化策略选取非支配排序遗传算法NSGA-Ⅱ[7]。NSGA-Ⅱ算法是NSGA算法的改进版，运算速度和准确性均有显著提高，为了标定分级快速非胜出排序后同级中不同元素的适应值，并尽可能均匀遍布，文献[7]提出了拥挤距离的概念，采用拥挤距离比较算子代替需要计算复杂的共享参数的适值共享方法。因此，优化问题可以表述如下：

公式（1）中：M为重量，Xi为设计变量;i为设计变量个数;Xil，Xiu为设计变量的上下限;λ为屈曲因子。该问题定义为无约束的非线性问题，结合遗传算法全局最优搜索能力和解决非线性问题的优势，优化模型得以求解。

2 算例

2.1 结构描述

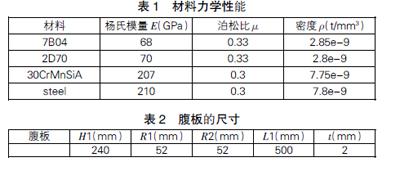
本文对某型飞机的金属加筋框板结构进行优化。框板结构如图2所示。

模型中腹板、上型材、筋条采用超硬铝合金7B04;下型材采用硬铝合金2D70;前脚盒、后脚盒采用中碳钢30 CrMnSiA;加载板采用普通钢。力学性能见表1。腹板结构尺寸见表2。

变量选择腹板厚度、下型材厚度、上型材厚度、筋条厚度、加载版厚度、内圆半径、外圆半径、下型材高度和上型材高度等变量。

2.2 有限元模型

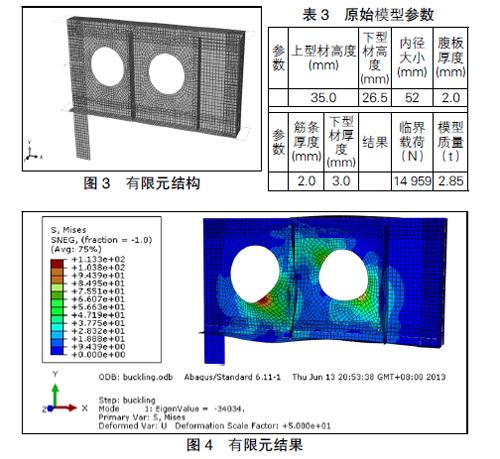
有限元模型如图3所示，利用结构的对称性仅仅创建了模型的右半侧，利用对称约束对模型的失稳特性进行仿真。单元的选取以线性四边形单元为主。由文献中仿真计算与实验结果对比发现，该建模方法计算精度高、收敛速度快。各零件之间的铆钉连接仿真采用Beam链接单元模拟，其作用同样是为了提高计算的精度和计算的效率。划分单元后模型的节点总数为5 768，单元总数为5 252，其中线性四边形单元总数为5 198，线性三角形单元数目为54。边界条件为右侧边界采用完全固支，上下边界限制Z轴方向的移动，左侧采用X轴的对称约束。载荷作用在左下角点处。原始模型参数见表3。

经过有限元计算结果如图4所示。

2.3 试验设计和近似模型

本次实验设计方法采用拉丁超立方。因素选择腹板厚度、下型材厚度、上型材厚度、筋条厚度、加载版厚度、内圆半径、外圆半径、下型材高度和上型材高度等变量。因素水平数选为3水平。通过实验设计的极差分析计算得到的Pareto图如图5、6所示。