动力学系统的同步问题及其控制器设计研究

许思遥 于懿 陈宇

摘 要 混沌系统作为一类特殊的动力学系统，它的同步问题在工程技术、生物学等领域受到极大重视。基于此，我们对Genesio混沌系统的同步问题进行研究。我们考虑Genesio系统在参数已知及参数未知情况下的同步控制器设计，然后通过 Lyapunov 稳定性分析使得所设计的控制器保证闭环系统的所有信号渐近稳定。最后我们通过 Matlab/Simulink 仿真实验验证所设计出的控制方法是有效的。

关键词 混沌系统;控制器;微分方程;同步

引言

混沌是指确定性动力学系统因对初值敏感而表现出的不可预测的、随机性运动[1-3]。混沌同步，从总体上说，属于混沌控制的范畴，它是指两个混沌系统在耦合作用下使其混沌运动达到一致的过程。许多混沌控制方法可以应用于混沌同步，反之亦然。1990年，美国海军实验室的L. M.Pecora和T. L. Carrol提出混沌自同步方法，首次利用驱动-响应法实现了两个混沌系统同步，从而拉开了混沌同步方法研究与应用的序幕[4-5]。混沌系统的同步问题在信息技术、保密通信等众多领域具有广泛的应用背景，从而受到了学者的广泛关注[6-8]。

正是由于这些原因，我们对Genesio混沌系统的同步问题进行研究，首先考虑Genesio系统在参数已知及参数未知情况下的同步控制器设计，然后通过Lyapunov稳定性分析使得所设计的控制器保证闭环系统的所有信号渐近稳定。最后，我们利用 Matlab/Simulink 仿真实验验证所设计出的控制方法是有效的。

1主要内容

本文主要研究一类混沌系统，其系统名称为Genesio系统，表达式如下：

其中a=6，b=2.92，c=1.2，系统混沌。

1.1 参数已知时Genesio系统的同步控制器设计

将两个初值不同的Genesio系统表示为驱动系统S1和响应系统S2：

（2-1）

（2-2）

其中u1，u2，u3为控制信号。

定义偏差

（2-3）

得到如下系统误差，

（2-4）

构造Lyapunov函数

（2-5）

其导数为

（2-6）

构造控制器：

（2-7）

将式（2-4）和式（2-7）代入式（2-6）得

（2-8）

此时满足条件：

（2-9）

根据Lyapunov稳定性理论，有

（2-10）

即加入控制信号后，驱动系统和响应系统可以有效地同步。

1.2 参数未知时Genesio系统的同步控制器设计

考虑驱动系统的参数已知，而响应系统的参数未知的情况。则驱动系统和响应系统写为

（2-11）

（2-12）

其中a1=6，b1=2.92，c1=1.2，a2，b2，c2未知。

定义偏差：

（2-13）

得到如下系统误差，

（2-14）

构造Lyapunov函数

（2-15）

其导数为

（2-16）

构造控制器

（2-17）

有m1>0，m2>0，m3>0。参数的自适应律为

（2-18）

将式（2-14）、式（2-17）和式（2-18）带入式（2-16）得

（2-19）

选取任意m1>0，m2>0，m3>-c1，m4，m5，m6>0则有

（2-20）

取m1=10，m2=10，m3=5，m4=m5=m6=1。

根据Lyapunov稳定性理论，系统误差（2-13）接近稳定，驱动系统和响应系统可以有效地同步。

1.3 Matlab仿真实验

（1）参数已知的Genesio系统

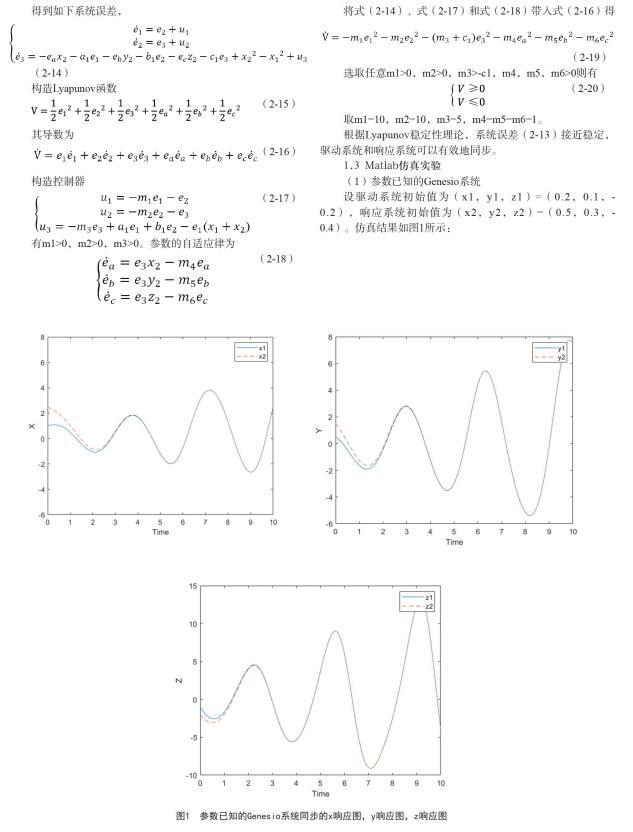
设驱动系统初始值为（x1，y1，z1）=（0.2，0.1，-0.2），响应系统初始值为（x2，y2，z2）=（0.5，0.3，-0.4）。仿真结果如图1所示：

根据仿真曲线我们看到，参数已知的两个Genesio系统的误差趋近于0，这表明所设计的控制器可以使参数已知的两个Genesio系统实现同步。

（2）参数未知的Genesio系统

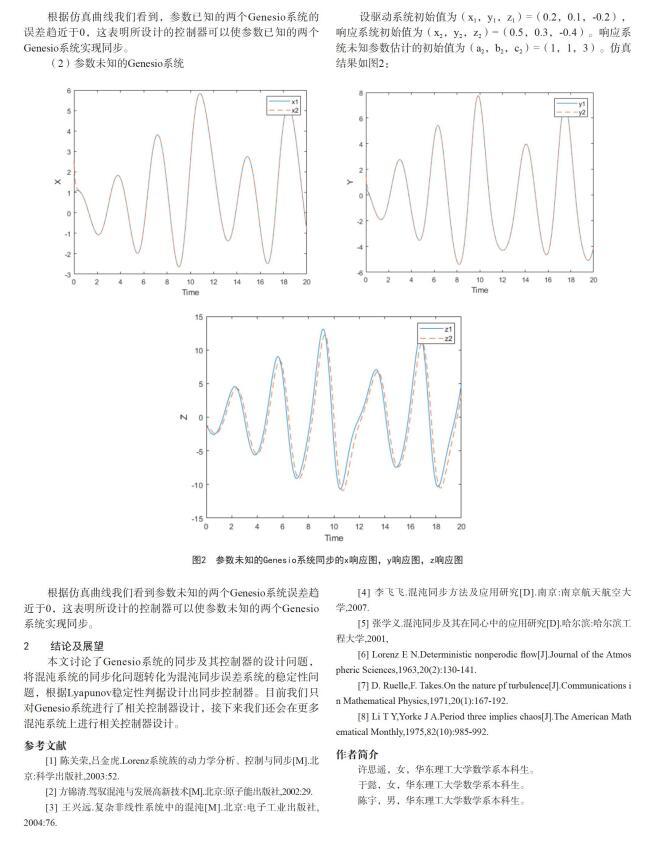
设驱动系统初始值为（x1，y1，z1）=（0.2，0.1，-0.2），响应系统初始值为（x2，y2，z2）=（0.5，0.3，-0.4）。响应系统未知参数估计的初始值为（a2，b2，c2）=（1，1，3）。仿真结果如图2：

根据仿真曲线我们看到参数未知的两个Genesio系统误差趋近于0，这表明所设计的控制器可以使参数未知的两个Genesio系统实现同步。

2结论及展望

本文讨论了Genesio系统的同步及其控制器的设计问题，将混沌系统的同步化问题转化为混沌同步误差系统的稳定性问题，根据Lyapunov稳定性判据设计出同步控制器。目前我们只对Genesio系统进行了相关控制器设计，接下来我们还会在更多混沌系统上进行相关控制器设计。

参考文献

[1] 陈关荣，吕金虎.Lorenz系统族的动力学分析、控制与同步[M].北京：科学出版社，2003：52.

[2] 方锦清.驾驭混沌与发展高新技术[M].北京：原子能出版社，2002：29.

[3] 王兴远.复杂非线性系统中的混沌[M].北京：电子工业出版社， 2004：76.

[4] 李飞飞.混沌同步方法及应用研究[D].南京：南京航天航空大学，2007.

[5] 张学义.混沌同步及其在同心中的应用研究[D].哈尔滨：哈尔滨工程大学，2001，

[6] Lorenz E N.Deterministic nonperodic flow[J].Journal of the Atmospheric Sciences，1963，20（2）：130-141.

[7] D. Ruelle，F. Takes.On the nature pf turbulence[J].Communications in Mathematical Physics，1971，20（1）：167-192.

[8] Li T Y，Yorke J A.Period three implies chaos[J].The American Mathematical Monthly，1975，82（10）：985-992.

作者簡介

许思遥，女，华东理工大学数学系本科生。

于懿，女，华东理工大学数学系本科生。

陈宇，男，华东理工大学数学系本科生。