钢丝绳复合套索具压制成形仿真研究

马 平，廖能解，欧建国，王志勇

（1.广东工业大学机电工程学院，广东 广州 510006；2 建峰索具有限公司，广东 广州 511356）

1 引言

钢丝绳索具是以钢丝绳为主要原材料，进行插编、压制等深加工，将钢丝绳的优越性能作进一步挖掘和发挥。钢丝绳压制索具是指钢丝绳端部经过弯制形成一定尺寸的环套，端部穿入铝套或钢套经模具压制与绳体固结在一起形成环眼的索具[1-2]。钢丝绳索具是工程吊装平台起柔性连接的关键部件，具有强度高、承载能力强、耐磨性好、挠性好等优点，因此广泛用于海洋工程、船舶运输、矿山机械、航空航天等领域，对我国重工业的快速发展起着重要的作用。

钢丝绳索具压制成形过程非常复杂，钢丝绳空间螺旋结构的复杂性决定了其受力的复杂性，它在工作过程中承受拉伸应力、弯曲应力、扭转应力和股内钢丝之间接触应力[3]。国内外学者建立了单捻钢丝绳有限元分析模型，分析了在轴向载荷作用下平直单捻钢丝绳的性能特性[4-6]。文献[7]建立了6X7+IWRC 钢丝绳数学模型，分析在不同载荷下钢丝绳绳芯的应变，并进行了试验验证。文献[8]通过采用有限元法建立了1×7 钢丝绳计算模型，模拟仿真的捻制成形钢丝残余应力与实验结果吻合。文献[9]进行了钢丝绳成形过程数值模拟和制品力学强度分析的研究工作，对简单直股和独立绳芯进行了应力分析。

传统钢丝绳索具都采用单一的钢套或铝合金套固结方式，钢套材质的高抗拉强度保证了钢丝绳索具拉力的要求，但由于钢性材质硬度高、压制时塑性变形小致使钢套不能完全与钢丝绳配合接触，不能抵抗索具高强度负载时的绳套固结处巨大剪应力；然而单一的铝合金套材质由于良好塑性变形能力，能与钢丝绳完全接触，保证了索具高强度负载时抗剪力能力，但同时降低了索具抗承载能力。因此整合钢套高的抗拉强度与铝合金套高的抗剪强度，提出复合型固结索具，即采用钢套加铝套的新型压制固结方式。根据钢丝绳是一种由钢丝捻制成股、股捻制成绳的空间螺旋体的特性，应用SolidWorks 建立1×7+IWS-24mm 型钢丝绳的几何模型，然后采用ABAQUS 软件并结合显示动力学方法对钢丝绳复合套不同间隙（0～5）mm 和复合方式（铝套-钢套、钢套-铝套）进行FEA 分析，为钢丝绳复合套索具的压制成形以及获得良好力学性能提供理论指导和支撑。

2 钢丝绳复合套索具结构特征与实体建模

以1X7+IWS-24mm 单股折返型钢丝绳复合压套索具为研究对象，IWS 代表独立钢芯结构，其芯丝、侧丝直径均为8mm，钢丝绳直径为24mm，捻向为右同向捻；钢套的长度为20mm，壁厚为9mm，铝套长度为50mm，壁厚也为9mm，在单一改变复合方式或间隙的同时复合套的尺寸参数保持不变。

基于SolidWorks 平台，采用参数化修改法建模方法建立1x7+IWS-24mm 单股折返式钢丝绳模型，相比完全程序法、曲线插入法等建模方法而言，该方法的优势是只需对某些特定的尺寸参数进行修改即可得到需要的模型，适合于建模过程繁琐、可变参量少的情况，整个建模过程方便高效，且得到的模型精确度高。然后将整个复合套钢丝绳索具各个部件分别进行独立建模，最后对钢丝绳、钢套、铝套和上下两个模具采用一系列配合约束完成装配。该1×7+IWS 单股复合套钢丝绳索具的几何模型，如图1 所示。

图1 钢套-铝套复合索具压制模型Fig.1 Sling Supression Model of Combination Steel-Aluminum Sets

拟采用单因素控制变量法分别改变间隙和复合套的复合方式来分析复合套索具成形过程中钢丝绳的应力分布特征，上下模具为对称结构，且压制成形后模具几乎不变形，其复合套钢丝绳索具的相关参数，如表1 所示。

表1 索具相关参数Tab.1 Parameters of Wire Rope Sling

3 有限元模型的建立

运用ABAQUS 软件对复合套索具进行成形仿真分析研究，首先采用Remove Faces 命令将模具实体模型转化为模具刚体壳模型，将大量的减少网格数量和计算机内存容量，以及提高计算效率。转化后的几何模型，如图2 所示。

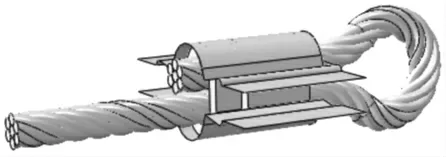
图2 钢套-铝套复合索具转化模型Fig.2 Sling Transform Model of Combination Steel-Aluminum Sets

钢丝绳索具压制成形过程非常复杂，属于高度非线性问题，首先由钢丝绳的点接触类型，逐渐演变为线接触，进而再转化为钢丝绳之间的面接触。而ABAQUS 显示动力学方法对处理接触条件变化的高度非线性问题非常有效，它的求解方法是在时间域中以很小的时间增量步向前推出结果，而无需在每一个增量步求解耦合的方程系统，或者生成总体刚度矩阵，对任意的拉格朗日—欧拉（ALE）自适应网格功能可以有效地模拟大变形非线性问题。因而应用ABAQUS 显示动力学方法，并采用ABAQUS/Explicit 模块中的General Contact 接触方式，可以准确的模拟压制成形过程中接触状态的变化。为了达到合理的仿真效果，需改变网格种子的大小，并采用Advancing Front 网格算法，该算法容易得到大小均匀单元网格，且网格可以与种子的位置良好的吻合，容易实现从粗网格到细网格的过渡。由于钢丝绳独特的空间螺旋特征，对钢丝绳采用8 节点六面体线性减缩积分（C3D8R）显示单元进行扫掠网格划分；复合套（钢套和铝套）结构规则，故均采用8 节点六面体线性减缩积分（C3D8R）显示单元进行结构化网格划分；刚体模具采用4 节点四面体线性单元（C3D4）进行自由网格划分。该1×7+IWS 单股复合套钢丝绳索具的有限元模型，如图3 所示。

图3 钢套-铝套复合索具压制有限元模型Fig.3 Sling Supression FEA Model of Combination Steel-Aluminum Sets

4 复合套索具压制成形应力分析

复合套之间的间隙（0～5）mm 和复合方式（铝套-钢套、钢套-铝套）都直接影响着钢丝绳的应力分布大小，从而影响钢丝绳的工作性能。因此，需要对其应力场分布进行分析研究，为了得到其应力分布特性，对钢丝绳索具进行FEA 分析。首先定义钢丝绳索具边界条件：下模具进行全约束，即约束6 个自由度，上模具采用Displacement 约束，对上模具施加向下的24mm 的位移载荷。然后运用Mises 屈服准则和Prandtl-Reuss 应力应变关系推导出弹塑性刚度矩阵，采用Augmented Lagrange method 算法计算，最后应用Dynamic Explicit 求解器对复合套索具（铝套-钢套、钢套-铝套）进行压制成形仿真求解。

4.1 铝套-钢套复合索具压制成形应力分析

铝套-钢套（钢套靠近环眼部位）复合套复合方式即将钢丝绳末端经过弯制先穿入钢套再穿入铝套，后经模具压制，与绳体固结在一起形成环眼的铝套-钢套复合钢丝绳索具。改变两者之间的间隙配合，从0mm 间隙依次增加1mm 直到增加到5mm 间隙。观察不同间隙情况下，钢丝绳在压制成型后其应力的分布特征和变化趋势。仿真分析结果，如图4～图5 所示。

图4 铝套-钢套复合索具、绳应力场（2mm 间隙）Fig.4 Stress Field of Combination Wire Rope Rigging of Aluminum-Steel Sets and Wire Rope（2mm Gap）

图5 钢丝绳最大应力值与复合套间隙的关系Fig.5 The Relationship between the Maximum Stress Value of Wire Rope and the Clearance of Composite Sleeve

通过对复合套（0～5）mm 间隙配合的分析发现，钢丝绳最大应力随间隙的增加呈“V”字型分布，在间隙为2mm 时，钢丝绳的最大应力值最小，为902.4MPa。由于钢丝绳应力大小和分布均匀性与疲劳寿命密切相关[10]。因此要以钢丝绳应力最小且分布均匀为原则，同时也需综合考虑复合套的应力分布，而行业中钢丝绳索具失效往往发生在钢丝绳上，复合套远远在安全范围内，故主要分析钢丝绳的内部应力分布情况。研究表明，钢丝绳复合套索具间隙为4mm 和5mm 时钢丝绳的最大应力值较大，2mm 间隙时最大应力值最小，故重点对比分析2mm、4mm、5mm 间隙时的钢丝绳内部应力分布情况。由于研究的钢丝绳模型为空间折返式，因而有钢丝绳直线段（下段）和折返段（上段）两部分，分别对以上3 种间隙各取钢丝绳截面径向的5 个特征点，分别为钢丝绳上段芯丝中心、钢丝绳上下两段压制后结合部左右两个钢丝中心、上下两段压制后结合部中间钢丝中心、下段芯丝中心。为便于分析不同间隙钢丝绳内部应力分布均匀性，对每种间隙的5 个特征点按描述顺序进行1 到5 序号编号，如图6～图7 所示。图6 中不同间隙的5 个特征点的应力值，其同一行左边数字代表特征点的节点编号，右边数字代表应力值。（如第一个特征点序号1 的866，872.786，其866 是该特征点的节点编号，872.786 为其应力值）。

图6 钢丝绳截面内部分布云图（2mm 间隙）Fig.6 The Internal Distribution Stress of the Wire Rope Section（2mm Gap）

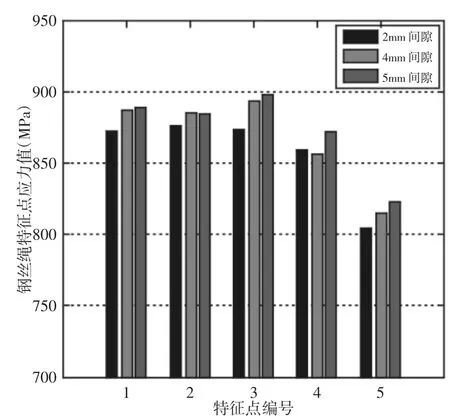
图7 不同间隙的同一截面五个特征点处钢丝绳内部应力值Fig.7 The Internal Stress Value of Wire Rope at Five Characteristic Points of the Same Section of Different Clearance

研究表明，钢丝绳压制完成后上段与下段钢丝绳接触处的钢丝应力较大，且上段芯丝比下段芯丝应力大。由图7 知，对比钢丝绳复合套间隙为2mm、4mm、5mm 时钢丝绳的应力分布特性，2mm 间隙内部各处应力均最小，且应力分布均匀，应力波动为8%。因此采用铝套-钢套复合方式，以钢丝绳应力最小且分布均匀为原则，则应选用2mm 间隙配合进行索具压制成形，此时钢丝绳应力最小且分布均匀，所以2mm 间隙时铝套-钢套复合钢丝绳索具有着良好的力学综合性能，能较好的满足工作要求。

4.2 钢套-铝套复合索具压制成形应力分析

钢套-铝套（铝套靠近环眼部位）复合套复合方式即将钢丝绳末端经过弯制先穿入铝套再穿入钢套，后经模具压制，与绳体固结在一起形成环眼的钢套-铝套复合钢丝绳索具。采用与铝套--钢套相同的研究方法即改变两者之间的间隙配合，从0mm间隙依次增加1mm 直到增加到5mm 间隙，进而分析研究此复合方式下压制成形后其钢丝绳随间隙的变化而产生的应力场分布情况。其应力分布情况，如图8～图9 所示。

图8 钢套-铝套复合索具、绳应力场（0mm 间隙）Fig.8 Stress Field of Combination Wire Rope Rigging of Steel-Aluminum Sets and Wire Rope（0mm Gap）

图9 钢丝绳最大应力值与复合套间隙的关系Fig.9 The Relationship Between the Maximum Stress Value of Wire Rope and the Clearance of Composite Sleeve

研究表明，钢套-铝套复合钢丝绳索具压制成形完成后，钢丝绳最大应力随间隙的增加呈“锯齿形” 递增，其配合间隙为0mm 时，钢丝绳的最大应力值为最小897.8MPa；与上文铝套--钢套研究方法相同，取钢丝绳最大应力值为最小时的0mm 间隙及最大应力值较大时的3mm 和5mm 间隙钢丝绳两段同一截面径向的5 个特征点，分析不同间隙钢丝绳内部应力分布均匀性，如图10～图11 所示。根据结果对比钢丝绳复合套间隙为0mm、3mm、5mm 时钢丝绳的截面应力分布，可知0mm 间隙钢丝绳内部各处应力均最小，且应力分布均匀，其芯部应力较大，偏离芯部钢丝绳应力减小，应力波动为6.4%。因此，采用钢套--铝套复合方式，则应选用0mm 间隙配合，并且与铝套--钢套复合方式下的2mm 间隙优选方案相比，其钢丝绳最大应力值减少4.6MPa，应力波动减少1.6%。因此经过两种复合方式的比较，应选用钢套--铝套“零间隙”复合方式进行压制成型，其工作力学性能会更好，在钢丝绳索具服役过程中将会更好的满足工作要求以及具有更长的疲劳寿命。

图10 钢丝绳截面内部分布云图（0mm 间隙）Fig.10 The Internal Distribution Stress of the Wire Rope Section（0mm Gap）

图11 不同间隙的同一截面五个特征点处钢丝绳内部应力值Fig.11 The Internal Stress Value of Wire Rope at Five Characteristic Points of the Same Section of Different Clearance

5 结论

（1）基于SolidWorks-ABAQUS 平台，建立1X7+IWS-24mm型单股折返式钢丝绳模型，并将模型导入到ABAQUS 中完成有限元模型的建立。

（2）采用铝套--钢套复合方式的钢丝绳索具压制成形后其应力结果显示，钢丝绳最大应力值随间隙的增加呈“V”字型分布，在2mm 间隙时其钢丝绳最大应力值最小为902.4MPa，且钢丝绳应力分布均匀，应力波动为8%。

（3）采用钢套--铝套的复合方式在不同间隙配合下压制成形后，其钢丝绳应力分布随间隙的增加呈“锯齿形”递增，其配合间隙为0mm 时，钢丝绳的最大应力值最小，为897.8MPa，且分布均匀，应力波动为6.4%。

（4）通过比较两种复合方式的优选方案，发现钢套--铝套复合 “零间隙” 配合索具压制成形后的钢丝绳最大应力值（897.8MPa） 比铝套-钢套复合2mm 间隙配合的钢丝绳最大应力值（902.4MPa）小4.6MPa，且应力波动减少1.6%。因此，采用钢套-铝套复合“零间隙”钢丝绳索具进行压制成型后其力学性能最佳，钢丝绳索具在服役过程中满足工作要求的同时将会有更长的使用寿命。