某推力矢量无人机优化控制分配策略研究

范林飞，王道波，刘孝成

(南京航空航天大学 自动化学院，江苏 南京 210016)

0 引言

本文设计的新型矢量推力无人机，通过操纵气动舵面出舵量和改变左右发动机推力轴线的方向来控制飞机的飞行姿态。所谓矢量推力技术，指的是通过喷管等装置改变发动机推力线的方向，从而将发动机推力沿轴向、法向和侧向进行分解，实现飞机的俯仰、滚转和偏航。两种控制结合起来能非常有效地改善飞机的操纵性。传统固定翼无人机单独依靠气动舵面偏转来控制无人机的状态，这种控制方式不适用于低速无人机，当飞机飞行速度较慢时，这种控制方式就显得较为乏力。本文在这种传统控制的基础上，加入矢量推力技术，设计了控制器，经过控制分配后无人机的动态性能和操纵性以及飞行品质大大提高。

1 新型推力矢量固定翼无人机结构设计及各模块功能介绍

如图1所示，所设计的无人机整个系统分为两大模块：以TMS320F28335处理器为核心，结合了多种传感器以及执行机构，用于通信数据的接收和发送，解析飞行数据的飞控系统；另外一个模块为地面监测系统，主要用于接收从飞机上下传的飞行参数，在界面上显示供操纵者观测。

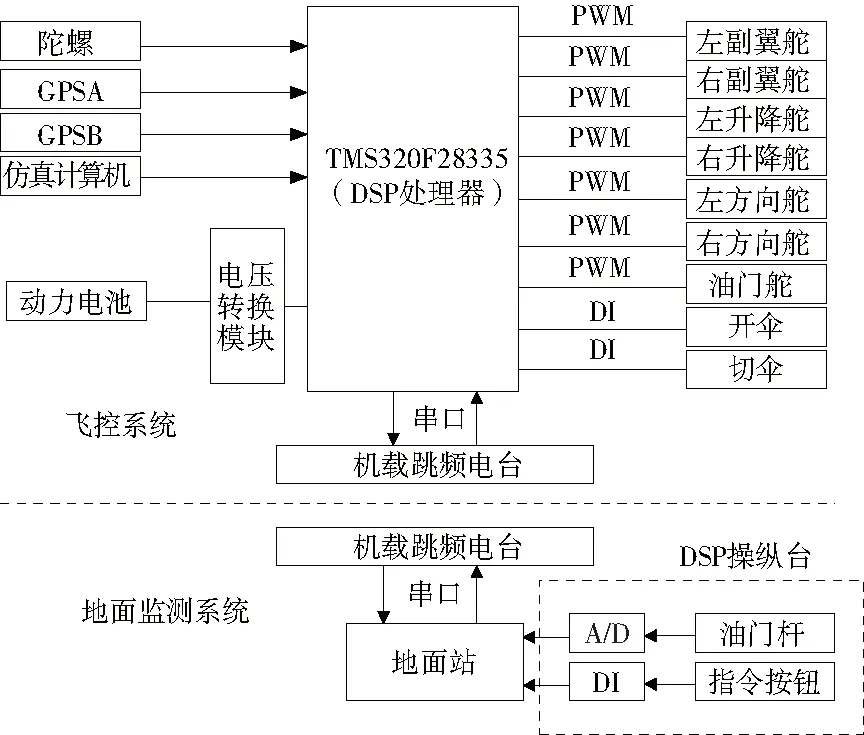
图1 无人机整体系统图

1.1 机载设备

该无人机机载设备主要有陀螺(IMU)、GPS、通讯电台动力电池和气压高度表等。其中陀螺和GPS是无人机的核心机载设备，在控制回路中作为传感器将飞机的姿态信息和位置信息反馈至输入端，从而实现无人机闭环控制[1]。采用GI550惯导来采集无人机的姿态信息，为保证无人机的精确定位，采用双GPS进行定位，GPS主要负责采集无人机的位置信息，包括经度、纬度、GPS高度等，此外还包括气压高度表、速度传感器等机载设备。

1.2 执行机构和通讯设备

无人机的执行机构主要为舵机。该无人机有8个舵面，其中尾轮舵用来控制无人机起飞滑跑时的侧滑方式，而无人机的推力则通过油门舵的开度来控制。动力电池采用+12 V，经电压转换模块将电压转换成+5 V来给飞控计算机供电。机载调频电台用来实现飞控计算机与地面站之间的通信数据传输。使用前需要对两个电台进行参数配置，包括通信方式、波特率、通讯速率、电台频段等参数的配置，飞控数据电台采用232串口与飞控计算机连接。

1.3 地面监测系统

地面监测系统主要用来检测无人机在空中飞行时的姿态、位置以及各机载设备工作时的信息。该系统主要由一台综显计算机、调频电台和DSP操纵箱组成。综显计算机软件界面是基于VC6.0编程环境下的MFC开发软件,其显示控件和输出控件均为NI Measurement Studio AppWizard控件。这些控件主要用来显示飞机的飞行参数、航迹规划以及地面站向飞控计算机发送的控制指令。这些指令通过DSP操纵台来发送，而飞控系统和地面检测系统之间数据则通过调频电台的无线电波进行传送和接收。

2 混合控制策略

无人机控制器整体结构控制采用串级控制，这样能很好地在无法建立比较精确数学模型的情况下研究无人机的控制规律。内回路为增稳回路和姿态回路，这是整个无人机控制的核心回路，外回路为位置回路。内回路通过不断逼近内回路期望的姿态角与传感器测得的实际角之间的误差来给出相应舵面偏角，以控制无人机的姿态。同时将角速率接入控制律，使系统的阻尼特性得到提升，形成一个增稳回路。外回路为位置控制，通过将GPS传输的位置信息反馈至输入端，不断修正位置误差，使其逐渐逼近期望值。整体控制框图如图2所示。无人机有俯仰、滚转和偏航三个通道，其中俯仰通道为纵向通道，滚转通道和航向通道为横侧向通道。下面分别从纵向和横侧向这两个通道来设计控制器。

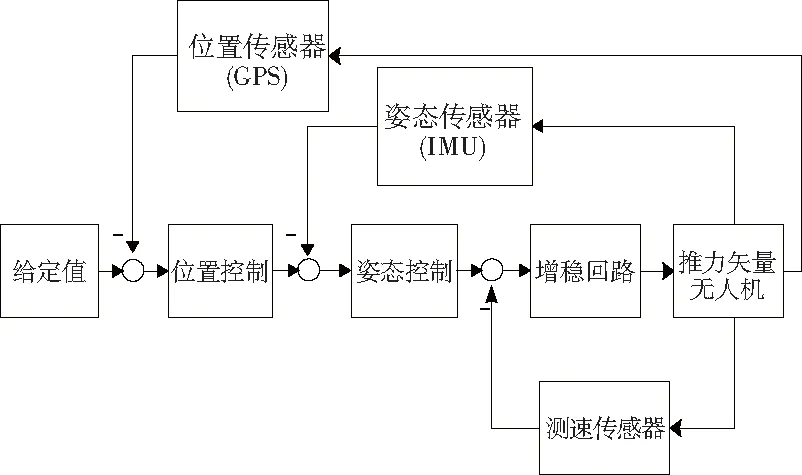
图2 整体控制框图

2.1 纵向混合控制

无人机纵向控制回路为俯仰角控制回路，回路采用闭环PID控制，同时为了增加系统的阻尼特性，将角速率反馈信号引入控制回路，使得飞机的整体动态性能更加完善[2]。从纵向通道来看，本文所研究的无人机在此基础上增加了矢量推力，改变无人机左、右两个发动机推力轴线的方向，从而对无人机质心产生俯仰力矩，使得飞机的姿态改变。气动舵面控制和矢量推力控制各自具有一定的控制权限，将两者结合使用，能有效地改善该无人机的控制性能。图3为纵向通道控制框图。

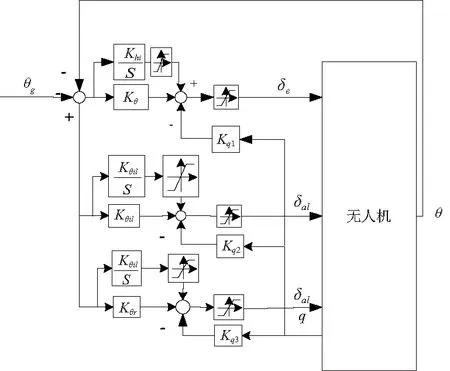
图3 俯仰姿态控制策略框图

如图3所示，该固定翼无人机俯仰姿态控制采用俯仰角和俯仰角速率闭环控制方式，使得无人机有着优良的阻尼特性，动态性能得到提高。控制律如下：

(1)

(2)

(3)

在控制回路中加入积分控制算法，若俯仰角的偏差较小时，积分能起到有效作用，当俯仰角偏差较大时，积分控制算法失效。上式中：δe为升降舵出舵量，可通过操纵地面站操纵杆来改变其出舵量；δal和δar分别为左发推力操纵量和右发推力操纵量，这三者对于固定翼无人机的俯仰姿态均具有一定操纵权限，共同控制使得无人机纵向通道的稳定性得到保障；q为由GI550陀螺采集的俯仰角速率；Kθ、Kθl、Kθr为比例系数；Kq1、Kq2和Kq3为俯仰角速率反馈系数；Khi、Kθil和Kθir为积分系数。

2.2 起飞横侧向姿态控制

该固定翼无人机为三点起落架式布局，后方有一个尾轮，通过舵机能控制其滑动方向，前面有两个前轮，通过发动机提供推力使得飞机在地面滑动，同时保持足够大升降舵出舵量和足够大迎角使得飞机在地面滑跑过程中能够产生足够大的升力来实现飞机的起飞。俯仰角度由地面测控站的操纵箱操纵俯仰杆控制升降舵出舵量来获取相应迎角，但要注意的是，要使得飞机俯仰角在约束范围内尽量保持飞机的姿态稳定，飞机的纵向俯仰力矩要能使得飞机平衡[3]。在起飞滑跑过程中，还要保持飞机在横侧向的姿态稳定性。通过在滑跑过程中操纵尾轮的转向δw和方向舵操纵量δd来保持无人机航向的稳定，从而减小无人机的侧滑位移，同时约束无人机滚转角，从而保持无人机在滑跑起飞过程中的平稳性。起飞横侧向姿态控制如图4所示。

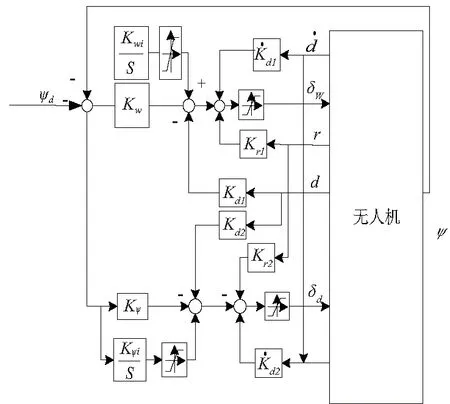
图4 起飞滑跑横侧向姿态控制

其控制律如下：

(4)

(5)

3 推力矢量无人机优化控制分配策略

在第2节中设计了推力矢量无人机纵向和起飞时横侧向控制策略，采用了气动舵面控制和推力矢量操纵混合控制。以纵向控制为例，常规无人机通过升降舵偏转来使得飞机的俯仰姿态发生变化，控制命令维数为1维，本文设计的无人机增加了左、右2个推力矢量操纵量机构，使得控制命令维数为3维，造成控制余度增加，输出端产生的控制量具有抽象性，相应舵面偏转量和左右推力矢量操纵量需要配置相应的加权系数才具有实际意义。假定控制器模块直接输出的虚拟指令为A，经过控制分配后的控制命令为B，实际系统命令为C，则这三者满足如下关系：

A(t)=gB(x,B,t)B(t)

(6)

gA(x,t)A(t)=gδ(x,t)δ(t)

(7)

式中：gA(x,t)为B和A函数关系；gB(x,B,t)为A的输入矩阵。忽略一些次要因素，利用泰勒公式将上述非线性方程线性化，得出A→B的线性化函数关系如下：

(8)

式中C为效率矩阵。实际控制分配问题为确定虚拟命令A和实际命令C之间的关系即加权系数的确定[4]。由上述分析可知，分配结果不唯一，因此需要合理运用优化控制分配方法来使得实际命令值逼近期望值。在无人机飞行中，常常将无人机动态性能指标和能量消耗量作为最终优化指标，将性能指标定义为D(x,B,t)，最终优化指标取其最小值。本文介绍一种线形规划方法：假设性能指标定义为D=fTx，∃E∈Rm×n,在Ex≤b的情况下，使得性能指标D取得最优值，此时的x即为所求B。其表达式如下：

(9)

EB≤b

(10)

其中不等式约束条件为左、右推力矢量操纵量限制δal、δar和升降舵出舵量限制δe。上述性能指标表达式及约束条件表示为：

(11)

-40°≤δe≤40°

(12)

-20°≤δal≤20°

(13)

-20°≤δar≤20°

(14)

因此不等式(10)中约束条件各项矩阵系数为：

(15)

(16)

其中B矩阵中的Ke、Kal、Kar为推力矢量操纵量和升降舵面权重系数，利用单纯形法可以有效求解上述矩阵的最优解[5-6]。目前基于关于单纯形法求解最优解的软件很多，只需输入矩阵系数即可很方便地求出上述线性规划问题的最优解。以纵向控制为例，将控制分配模块加入混合控制器中，重新设计纵向控制器如图5所示。

图5 优化控制分配后纵向控制器

其纵向控制表达式如下：

(17)

(18)

(19)

其选取原则以性能指标D达到最优指标为目标。由于横侧向控制优化分配设计与纵向控制原理相同，这里不再赘述。

4 飞控仿真实验

该固定翼无人机在飞行前需要通过仿真实验进行飞行质量评估，保证飞机正式飞行的品质。首先要确定控制器各个PID参数值，控制器中各个PID系数通过稳定边界法进行确定[7-8]，而气动舵面和左、右推力矢量加权系数的分配则根据上节提供的方法选取。以纵向控制为例，给定俯仰角θg=10°和θg=30°，分别得出无人机在无推力矢量作用和经过优化分配后推力矢量作用的仿真图如图6、图7所示。

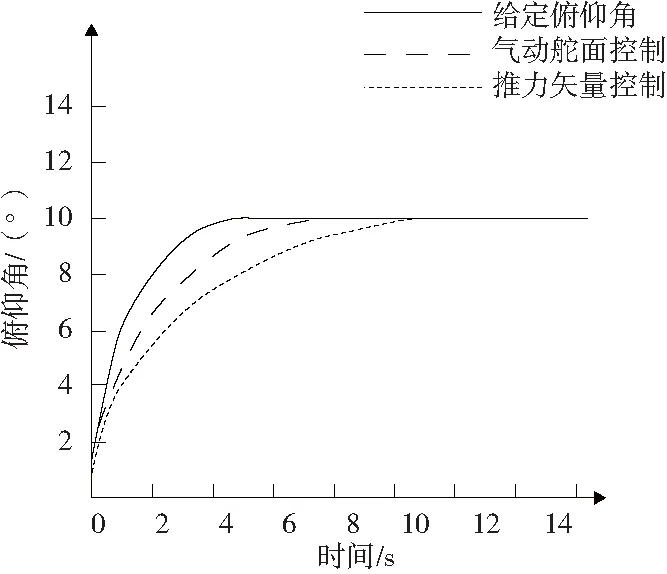
图6 俯仰角给定为10°时响应

由图6-图7对比可以看出：在俯仰角较小情况下，传统气动舵面控制和优化控制分配混合控制响应均无超调，但优化控制分配混合控制响应速度比传统气动舵面控制快很多，动态性能更好；在俯仰角较大情况下，传统气动舵面控制响应时间很长，且存在稳态误差；优化控制分配混合虽然存在超调量，响应速度很快，且无稳态误差。

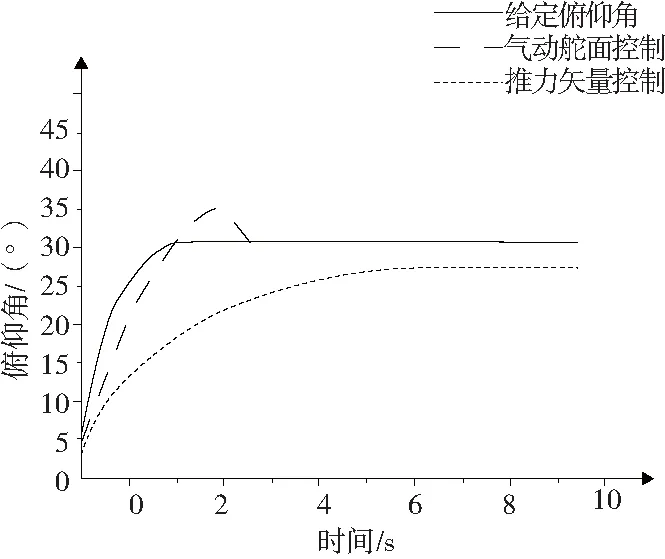
图7 俯仰角给定为30°时响应

5 结语

综上所述，经优化控制分配后的推力矢量无人机与传统气动舵面控制的无人机相比，在姿态角较大和较小时均不存在稳态误差，控制精度大大提高；同时响应速度相比传统气动舵面控制更快，推力矢量无人机的动态性能和稳态性能均有所提高，具有良好的飞行品质，能更好地完成相应的飞行任务。