矩阵式返向器与扁圆形返向器的动力学分析

刘明辉，范元勋

(南京理工大学 机械工程学院，江苏 南京 210094)

0 引言

现今应用较为普遍的返向器为扁圆形返向器与圆形返向器，其安装布置形式为通过螺母上沿圆周均匀分布的安装孔完成与滚珠和螺母的装配[1]。矩阵式返向器作为一种新型的返向器，不同于普通返向器的安装形式，它通过螺母轴向上的直槽插入螺母[2]，如图1所示。每个返向通道之间的距离为一个导程，且为一列分布。矩阵式返向器使得滚珠丝杠副螺母具有更小的轴向尺寸，滚珠丝杠副也因此更为紧凑，在航空航天伺服机构中有很大的应用前景。

图1 含矩阵式返向器的滚珠丝杠副模型 (局部)

目前，学者们已经对内循环滚珠丝杠副的返向器进行了动力学方面的研究与探讨。在对仿真模型的处理上，大多采取了部分模型简化的方式进行仿真，例如滚道形状简化[3]、返向器简化[4]和螺母简化[5]等，与实际使用情况相比仍有差距。本文将对原始的滚珠丝杠副模型进行仿真，比较分析两种返向器在相同工况下的接触特性，以获得更加贴合实际的研究结论。

1 内循环返向器回珠曲线建模

研究了一种应用于航天伺服控制系统的含矩阵式返向器的滚珠丝杠副，由北京某研究所提供。该型号滚珠丝杠副的基本结构参数如表1所示。

表1 滚珠丝杠副结构参数

返向器的回珠曲线是影响滚珠运动循环流畅性的决定性因素之一[6]。本文中两种返向器皆采用五次抛物线型回珠曲线，函数关系为[7]：

(1)

式中：θ为等距曲面方程的参数角，rad；ρ是球心到丝杠轴线的距离，ρ=ρ(x)，mm；系数A、B、C可由式(2)计算得到。

可解得系数A、B、C的关系式为：

(2)

(3)

式中：xF为回珠曲线与螺旋线交点的x坐标；λ为螺旋升角，rad。

根据五次抛物线型回珠曲线的设计方法，回珠曲线上点到轴的距离ρ可用偏离量υ表示，即

(4)

由于该曲线的对称性，只需计算滚珠沿丝杠滚道爬升段、翻越丝杠滚道牙顶圆角段和经过丝杠滚道牙顶段3段曲线上ρ的值。其中，在每段曲线上回珠曲线到螺旋轴的距离ρ与偏离量υ的对应关系如表2所示。

表2 回珠曲线上的点到螺旋轴的距离ρ与偏离量υ的对应关系 单位：mm

其中: 偏离量υa、υb与α1的计算公式为：

(5)

(6)

在MATLAB中编写上述函数关系并代入相关参数，并按以下顺序进行求解：

1) 根据公式(3)求出xF的值；

2) 通过公式(2)求出系数A、B、C；

3) 通过公式(5)求出υa与υb，通过公式(4)计算得到每段曲线交界处的x的值；

4) 通过表2中偏离量υ的取值范围得到每段回珠曲线中x的区间。

MATLAB计算的参数值如表3所示，五次抛物线型回珠曲线如图2所示。

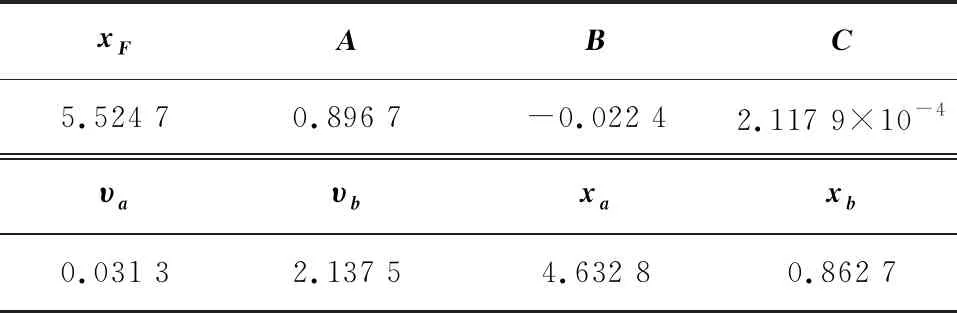
表3 返向器回珠曲线相关参数表

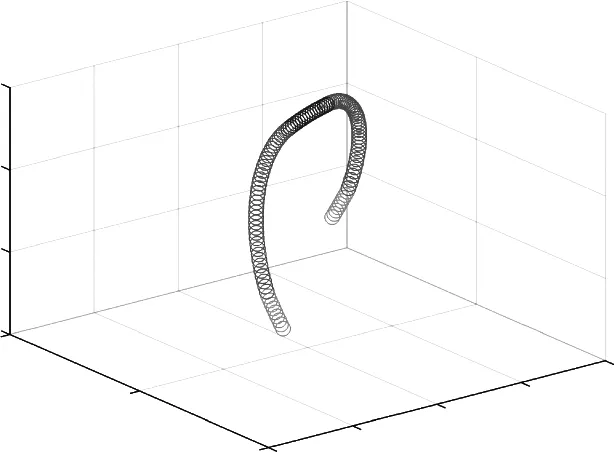
图2 MATLAB中生成的五次抛物线型回珠曲线

2 滚珠丝杠副的动力学分析

2.1 滚珠丝杠副建模

在Creo 3.0中完成丝杠、螺母、滚珠链和返向器的建模，并按照顺序进行装配[8]，将模型另保存为Parasolid(.x_t)格式。除返向器以及对应的螺母结构不同外，其余的尺寸参数皆相同。其中，矩阵式返向器模型如图3(a)所示，扁圆形返向器模型如图3(b)所示；两种滚珠丝杠副模型分别如图4(a)、图4(b)所示。

图3 两种返向器模型

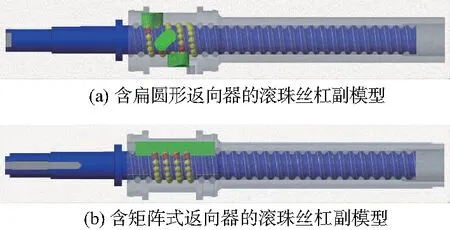
图4 两种滚珠丝杠副装配模型

2.2 基于ADAMS的动力学仿真

首先，在ADAMS中导入2.1节里创建的Parasolid(.x_t)文件，设定滚珠丝杠副各部分的材料属性如下：丝杠、螺母、返向器、滚珠的材料均为钢，各零件的弹性模量、泊松比、密度数值相同，分别为2.07×105MPa、0.29、7.8×10-6kg·mm-3。

然后给各个构件之间添加约束与接触，如表4所示。

表4 滚珠丝杠副约束与接触设置

最后对转动副添加驱动，对螺母端部施加轴向力并进行仿真。驱动角速度曲线如图5所示。图5中，在螺母位移相同的前提条件下设置不同转速条件下的仿真时间。

图5 丝杠驱动角速度曲线

根据含矩阵式返向器的滚珠丝杠副的实际使用工况，设定滚珠丝杠副在ADAMS中进行动力学仿真的4种工况条件，如表5所示。通过不同工况下对比分析使得返向器的性能分析更加贴合实际。

表5 滚珠丝杠副仿真工况

3 滚珠对两种返向器的碰撞仿真分析

在高速、重载工况下，返向装置受到滚珠循环、连续、快速的碰撞接触和摩擦影响，导致返向装置所受载荷高频变化，工作温升较快；在产生低频噪声与振动的同时，容易引发摩擦磨损、蠕变松弛、力学致热、疲劳、屈服失效等各种力学失效现象，是影响滚珠丝杠副寿命的主要原因[9-10]。因此，有必要分析不同工况下滚珠对返向器的碰撞力的变化情况。

各工况下滚珠对返向器的接触碰撞力仿真曲线如图6、图7、图9和图10所示。将各工况下的碰撞力曲线导入MATLAB中得到滚珠对返向器的接触碰撞力峰值，如表6所示。

表6 不同工况下滚珠对返向器的接触碰撞力

以下将含矩阵式返向器的滚珠丝杠副简称为Model 1，将含扁圆形返向器的滚珠丝杠副简称为Model 2。选取滚珠链的第一圈中最先进入返向器的一颗滚珠为研究对象，分析其循环运动过程中与返向器的接触特性。

3.1 转速对滚珠碰撞力的影响

当滚珠丝杠副受到恒定轴向力时，滚珠在额定转速和低转速工况下对返向器的碰撞力是不同的。

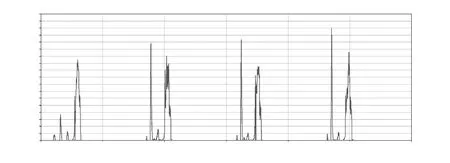
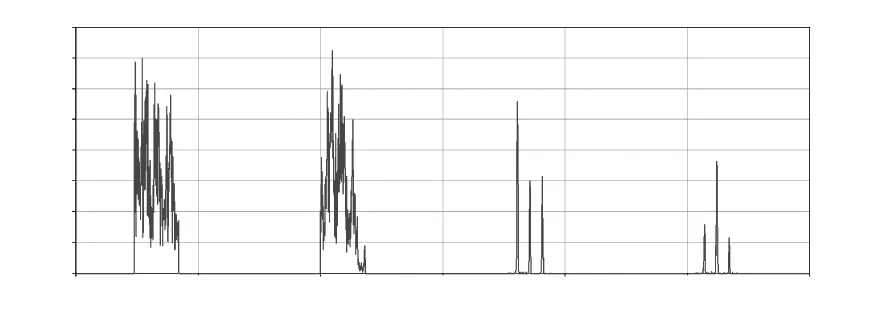
图6 低速常载工况

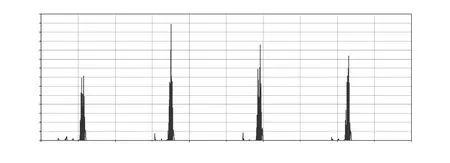
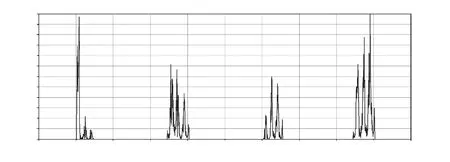
图7 额定转速工况

结合表6和图6(a)，当滚珠进出返向器时，会产生较大的冲击碰撞力,在滚珠翻越丝杠滚道顶部时产生的碰撞力较小，即碰撞力分段现象。由图7(b)和表6可知，额定转速下滚珠对扁圆形返向器的碰撞力略大于低转速下的碰撞力。

随着转速的增加，滚珠对矩阵式返向器的碰撞力增加量约为245 N，增加率为61.25%；滚珠对扁圆形返向器碰撞力的增加量为11 N，增加率为61.11%。

结合表6和图6(b)可知，滚珠对扁圆形返向器的碰撞力在ns=400r/min时有递减的趋势，这是由于丝杠转速较低，在0.1s后，即丝杠转速达到恒定转速后，出现滚珠运动的不连贯造成的，如图8所示。

滚珠进入返向器推力主要来自于后面的滚珠。转速较低时，滚珠与滚珠之间的间隙使得后面滚珠与前面滚珠的接触时间较长，导致滚珠的入射速度降低，滚珠对返向器入口处的碰撞力减小。

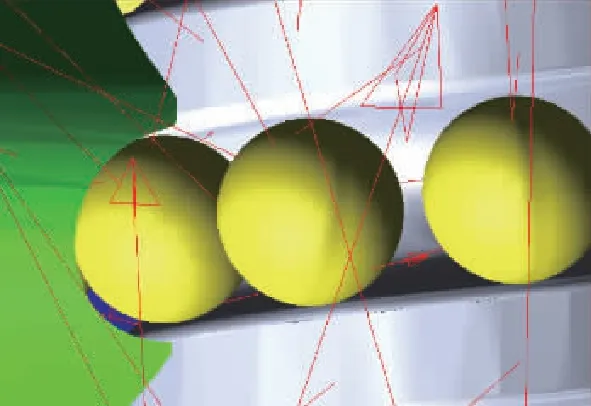
图8 运动过程中滚珠与滚珠之间的 间隙图

3.2 轴向力对滚珠碰撞力的影响

该种含矩阵式返向器的滚珠丝杠副在实际使用中受到恒定轴向力。在轴向力作用下，滚珠的运动与受力状态将发生改变，对返向器的冲击碰撞也会产生较大影响。

结合表6和图10可以看出，当滚珠丝杠副无轴向力作用，且驱动转速ns=1 220r/min时，滚珠对两种返向器的碰撞力皆<1N。

结合表6、图6和图9可知，在转速恒定条件下，滚珠对矩阵式和扁圆形返向器的碰撞力随着轴向力的增加而增大。随着轴向力的增加，滚珠对矩阵式返向器的碰撞力的增加量为118 N，增加率为29.5%；滚珠对扁圆形返向器碰撞力的增加量为69 N，增加率为383%。

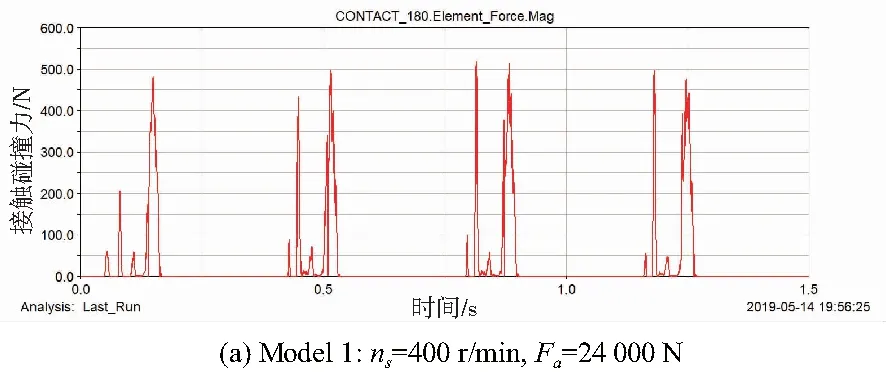
图9 低速重载工况

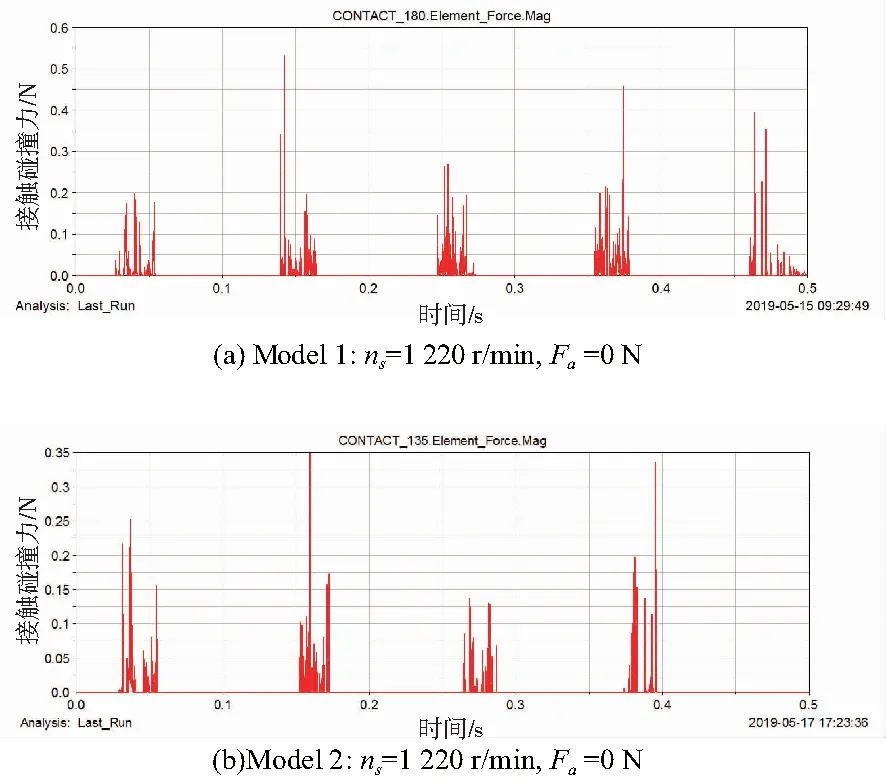
图10 对比工况

4 结语

1) 从位置结构方面，扁圆形返向器的轴向间距为1.5倍节距，而矩阵式返向器每个返向通道的中心距离为单倍节距，因此矩阵式返向器所需的螺母尺寸更小，该种滚珠丝杠副的结构更紧凑。

2) 由动力学分析可知，在不同工况下，滚珠对两种返向器的碰撞力皆随着转速和轴向力的增加而增大；相同的工况下，滚珠对矩阵式返向器的碰撞力明显大于滚珠对扁圆形返向器的碰撞力，但轴向力对扁圆形返向器的增加率远大于矩阵式返向器。因此，含矩阵式返向器的滚珠丝杠副更适合于结构紧凑且短时工作的机构中，同时，在突变的工况下拥有更好的传动平稳性。