基于BAS算法的河渠突发水污染溯源

王忠慧，贡 力,2，康春涛，王 鸿，杨轶群

(1.兰州交通大学土木工程学院，甘肃 兰州 730070;2.兰州交通大学调水工程及输水安全研究所，甘肃 兰州 730070)

突发水污染事件会使整个水生态环境遭到破坏，从而造成巨大的损失，甚至会引发社会动荡，需采取必要的应急措施来应对[1-2]。在水污染事件发生的第一时间判断出污染源的位置、掌握其污染物的源强、获知污染事件发生的时间[3]，是处理这种不确定性问题的关键所在，而能否快速有效地找到污染源的位置决定着能否最大限度减小突发水污染事件影响的范围[4]。

突发水污染事情追踪溯源就是了解水污染发生以及发展的全过程，而源项信息的识别尤其关键，国内外在源项信息识别方面已取得了很多研究成果，但还没有形成一个完整的解决突发水污染事情溯源问题的体系。源项信息识别常用的方法有确定性方法、概率统计方法和耦合的概率密度分析方法3类[5]。在确定性方法研究方面，辛小康等[6]通过遗传算法与数学模型相结合的方法，对一维单点源单变量和多点源多变量问题分别进行了研究；Boano等[7]利用地质统计法有效恢复了任意分布源和多个独立点源的水污染释放历史；曹宏桂等[8]将水污染问题利用有限元法进行正演，用PSO-DE混合优化算法结合移动监测平台进行反演，证明了该优化算法在二维水环境下的适用性。确定性方法最大的特点是利用一组最优的污染物浓度信息求解污染源项；缺点是计算量较大且没有充分考虑数据的不确定性，而且当信息不准确时往往结果误差很大。在概率统计方法研究方面，陈海洋等[9]在考虑有限宽度河流瞬时岸边污染泄漏的情况下，建立了水体污染识别数学模型，并以典型Metropolis算法构建马尔科夫链取得后验概率分布；姜继平等[10]通过Adaptive Metropolis算法对后验概率密度进行采样，得到了操作参数推荐值，为贝叶斯推理技术的应用作出了重要贡献；Wei等[11]通过分析正向模型的不确定性，结合AM算法对假想的河道排放污染物源项进行了反演。概率统计方法的应用主要是考虑到了突发水污染事件的不确定性，虽然能得到污染源项的“可能解”，但是计算时抽样过程极为耗时且结果对随机变量的分布信息过于依赖。在耦合的概率密度分析方法研究方面，早期的逆向概率密度函数来自地下水污染的研究，Neupauer等[12]研究表明，在一维和二维环境下的地下水，可以用逆向概率密度函数求得源项的位置和时间信息；程伟平等[13]将水污染释放过程重构，通过对比传统的优化方法与逆向概率密度的优化方法，结果表明逆向概率密度优化方法减少了计算量，提高了计算效率；王家彪等[14]提出结合概率密度分析的微分进化法对突发水污染事情进行溯源研究。耦合的概率密度分析方法通过实现源项信息之间的解耦，确保在计算过程中计算量不会过大，也能考虑到突发水污染事件的不确定性，是确定性方法和概率方法的结合。耦合的概率密度分析方法不仅简化了水污染溯源的过程，而且提高了溯源精度，是新一代的溯源研究方法。

本文采用耦合的概率密度分析方法，将突发水污染溯源的模型简化，利用天牛须搜索(beetle antennae search，BAS)算法[14]识别一维河渠污染物源项，并通过Matlab进行模型仿真试验来验证BAS算法的可行性及应用前景。

1 数学模型

水污染溯源问题就是通过已检测到的固定时刻的质量浓度信息确定污染源位置x、排放时刻t及源强m03个污染物源项[15]。本文通过水力学计算方法，利用正向质量浓度概率密度函数(污染物从污染源传播到下游某一断面的概率)与逆向位置概率密度函数(从观测者角度出发，由观测断面判断污染物可能来自任意位置的概率)之间的关系，实现源项3个未知量之间的解耦，进而通过质量浓度与位置概率密度函数之间的相关关系以及质量浓度与正向质量浓度概率密度函数之间的关系，构建水力学模型。

假设河渠在长度方向上远远大于宽度和深度方向，则污染物排入水体后能在短时间内与水体混合均匀，并且水流流速与污染物质量浓度均匀分布。在污染物只随流程方向变化的情况下，污染物输移数学模型可以简化为一维的水流水质耦合模型[16]，计算公式为

(1)

式中：ρ(x,t)为污染物在x断面t时刻的平均质量浓度，mg/L；u为河渠断面平均流速，m/s；E为渠道纵向离散系数，m2/s；K为污染物降解系数，s-1。

若水污染的排放形式为瞬时排放，则污染源以下河渠中的污染物质量浓度随河长的变化规律为

ρ(x,t)=

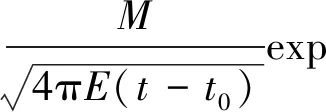
(2)

式中：M为瞬时排放的污染物面源强度，即源强，g/m2；x0为污染物排放位置，m；t0为污染物排放时间，s。

任何形式的水污染在河渠输移过程中都可以用两种概率密度函数来表示：一种表示污染物在河渠中的质量浓度分布，为正向质量浓度概率密度函数，即污染物从源头传播到下游某一位置的质量浓度分布概率；另一种表示从观测断面判断污染物可能在上游的某个断面，为逆向位置概率密度函数，反映污染物在不同位置的可能性大小。而耦合的概率密度分析方法就是通过对比发现正向质量浓度概率密度函数与逆向位置概率密度函数之间的关系，实现污染物排放位置、时间和源强之间的解耦。

该方法起初用于对地下水的研究，Neupauer等[17]得到了一维地下水域条件下正向质量浓度概率密度与逆向位置概率密度之间的关系：

(3)

式中：P为t′时刻从断面x2推断污染物的源头位置x1处的逆向位置概率密度，具有m-1的量纲；t′为逆向计算时间点；P′为t时刻污染物由x1断面输移到x2断面的正向质量浓度概率密度，也具有m-1的量纲。

因为P与P′具有相同的量纲，分别表示逆向位置概率密度输送过程与正向质量浓度概率密度输送过程，两者之间是相互伴随的过程，所以两者之间具有高度的耦合性，即下游给定断面观测到的质量浓度过程与污染源在某一时刻出现在某一位置的概率相对应。

由式(2)(3)可推导得出逆向的位置概率密度为

P(x1,x2,t′)=

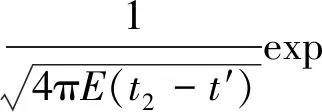
(4)

式中t2-t′为污染物从x1断面(源头位置)到x2断面所用的时间。

由式(4)可知在污染源位置和释放时间信息已知的情况下，就可以计算得到逆向位置概率密度P。

2 优化模型

2.1 优化模型的构建

由式(3)可知，逆向位置概率密度P与观测的质量浓度系列ρ之间线性相关，其相关系数r=1。相关系数的表达式为

(5)

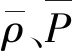
优化模型建立的目的就是寻找最优解，既然逆向位置概率密度函数已经实现了污染源排放位置、时间和源强之间的解耦，便可以先从水污染现场推测得到的一系列污染物排放位置、时间，即x′0、t′0中寻优，确定最优的x′0、t′0为x0和t0，再计算得到M。

根据观测的质量浓度系列ρi，假定的x′0、t′0以及对应时刻的质量浓度信息得到Pi的表达式，构造目标函数如式(6)所示。对于目标函数式(6)，当且仅当x′0=x0、t′0=t0时，相关系数r=1，此时目标函数达到最优状态。

min(1-r)

(6)

由式(6)得到污染物排放位置和时间，则源强M可由下式大致推算：

(7)

然后利用正向质量浓度概率密度函数与质量浓度信息之间的关系，进一步构建优化模型计算最终源强，其目标函数为

(8)

2.2 优化模型的求解

本文使用BAS算法求解一维河渠稳态点源扩散模型，该算法是2017年提出的一种高效的智能优化算法[18]，它通过模拟天牛搜索食物的过程进行优化计算。天牛是甲虫一族，它最大的特征是拥有两只比身体还要长的触角(须)，当天牛觅食的时候，利用两须搜索食物气味，通过食物的气味(也就是目标函数)控制移动行为和转向行为来搜索食物，当天牛搜索到食物的时候也就是计算得到最终的优化结果的时候。为了使模型的计算结果精确，本文将BAS算法中的步长进行改进，采用变步长的BAS算法求解模型，随着步长的减小，算法的计算速度由快变慢，完成从全局到局部寻优的一个过程，可以有效缩短算法的收敛速度，提高算法的计算精度。具体计算步骤如下：

步骤1：确定优化模型的目标函数(式(6)(8))。

步骤2：以al表示左须位置，ar表示右须位置，o表示质心，用d0表示两须之间的距离。假设天牛头朝向任意，因而从天牛右须指向左须的向量朝向也是任意的，由归一化的随机向量l表示：

(9)

式中:rands(m,1)为一随机向量，与天牛须的指向有关；m为维数，即目标函数未知数的个数。

步骤3：经过G次迭代后，天牛左右两须的位置可以根据l确定为

(10)

式中：aG为第G次迭代后质心的位置；dG为第G次迭代时天牛两须的距离。

步骤4：由左右两须的适应值确定天牛下一时刻的位置坐标；

aG=aG-1+slsign[f(al)-f(ar)]

(11)

其中

s=cd0

式中：s为步长；c为常数；f(al)为al的适应度值，表示向左走；f(ar)为ar的适应度值，表示向右走；sign为符号函数，若f(al)f(ar)，此时天牛向右须方向移动。每进行一次迭代，搜索距离和步长的变化如下：

dG=η1dG-1+d0

(12)

sG=η2sG-1

(13)

式中η1、η2分别是搜索距离更新系数与步长衰减系数。

步骤5：将步骤4计算得到的aG代入目标函数式中，直到找到目标函数的最优解或达到最大迭代次数，结束迭代。

BAS算法流程如图1所示。

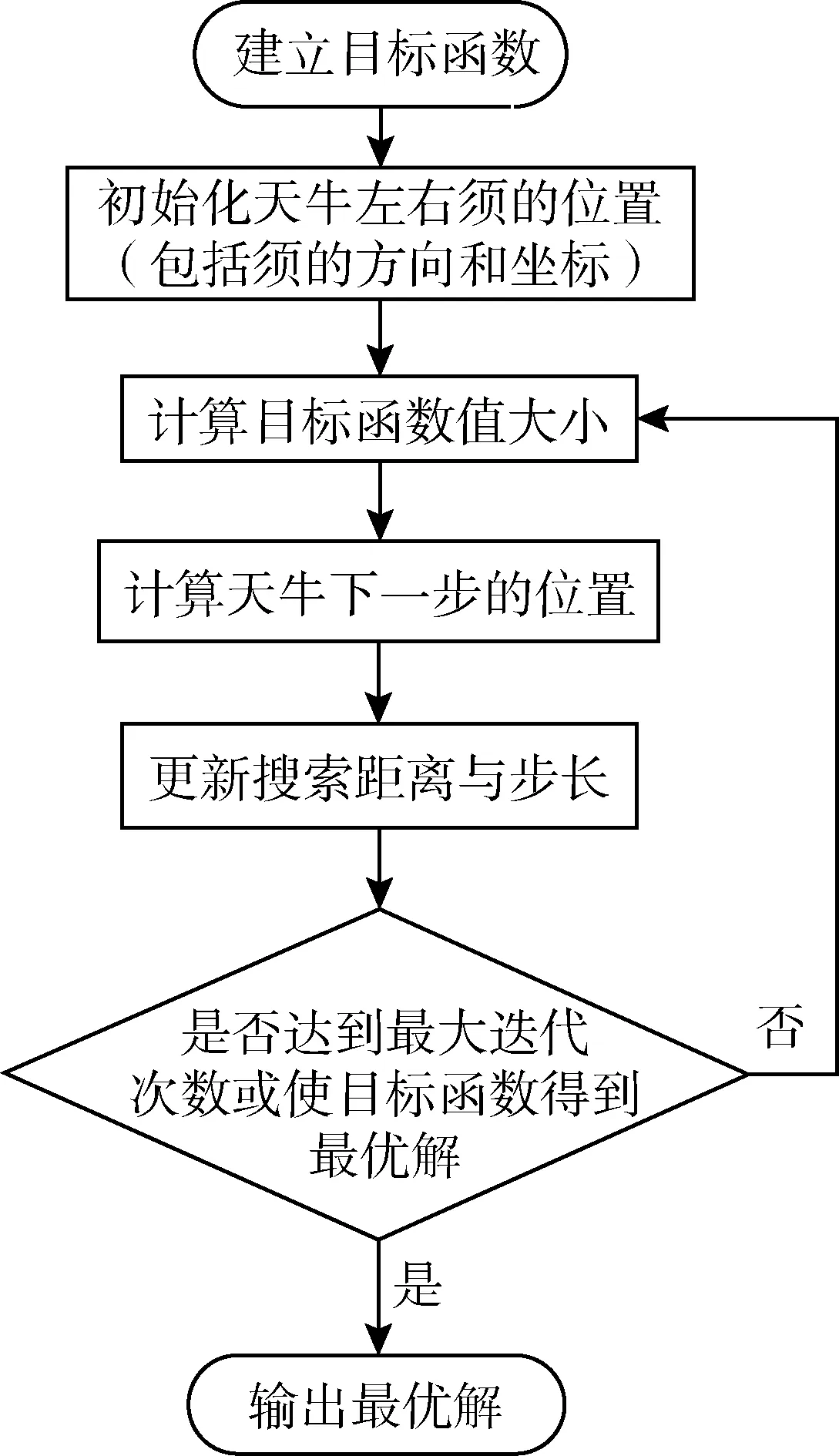
图1 BAS算法流程Fig.1 BAS algorithm flow chart

3 模型仿真试验

综合考虑了南水北调中线[19]、引大入秦输水渠道等一些实际河渠的基本输水状况后，选定一段没有支流汇入或突然涌泄水的、可视为一维恒定流进行计算的矩形断面的河渠进行仿真试验。河渠为浆砌块石护面，糙率系数为0.025，底宽为10 m，水深 4 m，坡降0.002 8%，流速0.36 m/s，河渠纵向离散系数为2.0 m2/s。假设上午9:00在A断面处(假定此处为坐标原点)瞬时排入1 000 kg的污染物，为了便于对比分析污染物的质量浓度变化过程以及验证BAS算法的计算结果，在下游河道设置了距A点800 m和1 200 m的A1和A2两个监测断面。根据污染物扩散模型(式(2))，在不考虑降解作用的情况下，分别计算两个断面的质量浓度过程，并在得到的计算结果中人为加入10%的观测误差(也就是在污染物扩散模型中得到的质量浓度数据中加入10%以内的变幅)，生成污染物质量浓度变化过程如表1所示。

为便于说明BAS算法计算本文优化模型的可行性，将得到的两断面质量浓度信息分别进行两次水污染溯源计算。选择Matlab软件进行模型仿真计算，取初始步长为1 000，迭代200次，再进行50次计算求取平均值后，得到计算结果如表2 所示。

从表2可看出，由A1断面计算得到的污染物质量为975.72 kg，与实际值相比误差为2.43%，计算得到的排放位置差25.43 m，排放时间超出7 min；由A2断面计算得到的污染物质量为964.32 kg，与实际值的误差为3.57%，计算得到的排放位置差56.22 m，排放时间超出9 min。通过不同观测断面的两次计算结果发现，由A1断面的浓度信息计算得到的源项信息的精度比A2断面高。因为在计算过程中没有考虑降解作用，所以不能从水力学的角度来分析误差。考虑到BAS算法在计算时对初始步长的选取具有一定的随机性,并且通过多次计算发现当初始步长在大于自变量2/3的范围内取值时，计算结果的精度较高。由于两个断面所求的污染物排放位置和时间(即自变量)范围不同，A2断面的自变量范围较A1断面大，因此，初始步长为 1 000时，对于A2断面来说，得到的溯源精度就没有A1断面高。在实际发生突发水污染事情时，可以通过现场考察或是通过已有的资料分析得到自变量的大致范围，再计算源项，便可得到更加精准的污染物排放位置和时间。

表1 人工生成的观测断面污染物质量浓度Table 1 Mass concentration information in observed section

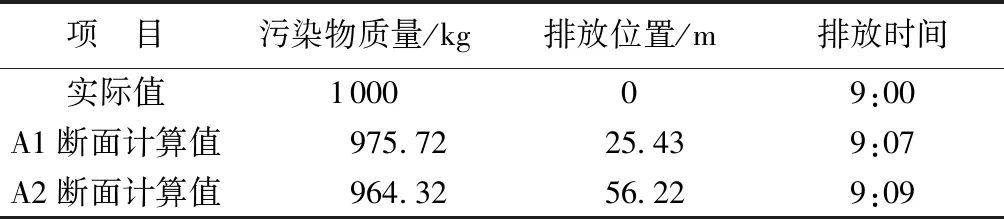
表2 仿真溯源结果Table 2 Table of simulation traceability results

为了测试溯源结果的准确性，把由A1断面计算得到的源项信息代入污染物扩散模型(式(2))中，得到污染物在A1断面处的计算质量浓度变化过程；将计算质量浓度变化过程与观测质量浓度变化过程进行比较(图2)可知，在质量浓度未达到峰值之前计算质量浓度较观测质量浓度高，但质量浓度达到峰值之后，观测质量浓度系列比计算质量浓度系列大。总体上，两条曲线的相关性较高，溯源的计算结果具有较高的精度，因此溯源模型重构的突发水污染事件能够反映实际水污染全过程。

为说明BAS算法在突发水污染溯源计算中的特点，在模型仿真试验中采用粒子群算法(partical swarm optimization，PSO)进行了计算，结果表明，同样取50次计算结果的平均值，PSO算法的精度比BAS算法高。但进一步分析发现BAS算法在迭代了106次之后趋于稳定，而PSO算法迭代了564次后才趋于稳定；BAS算法计算50次后取平均值的计算精度与PSO算法计算42次后取平均值的计算精度相同，但BAS算法所用的总计算时间为30 s，而PSO算法为125 s。可见BAS算法的单次计算精度比PSO算法低，但是BAS算法收敛速度快，达到相同的计算精度BAS算法所用的计算时长也明显低于PSO算法。

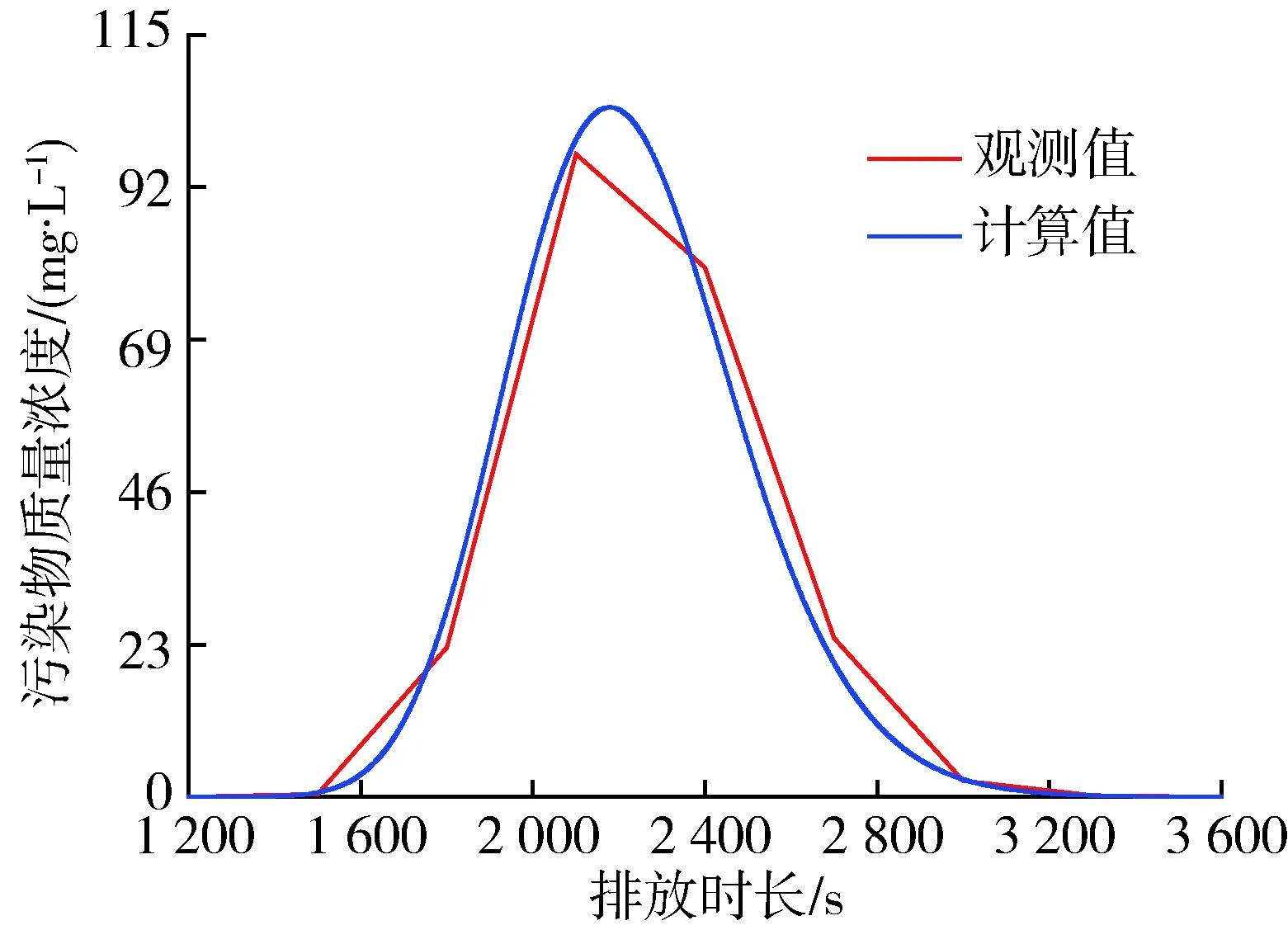
图2 A1断面污物物质量浓度过程Fig.2 Concentration process diagram of A1 section

总体来说，BAS算法计算结果精度高，收敛速度快，算法简单，在将来的基于污染物源项解耦的突发水污染溯源方面有较好的应用前景。但BAS算法在计算过程中步长一直在随着迭代次数的增加而减小，无论能否进一步找到最优位置，步长一直在衰减，缺少一种反馈机制，这也是BAS算法在水污染溯源研究中有待提高的地方。

4 结 语

本文利用耦合的概率密度分析方法将一维水力学条件下的正向的质量浓度信息与逆向的位置信息进行解耦，构建了污染物排放时间、位置和源强解耦后的水力学模型。将优化后的水力学模型利用BAS算法进行模型仿真计算，发现BAS算法可以很好地实现源项信息的求解；通过不同断面的溯源计算以及与PSO算法进行比较，结果表明BAS算法收敛速度快，运算量小，但是步长具有衰减性，不管每一步计算得到的结果是否变得更优，步长总会衰减，但多次求取平均值后可以达到计算精度要求。本文论证了BAS算法在突发水污染溯源领域的可行性，拓宽了BAS算法的应用领域，但是对于复杂的水力学模型以及更高维问题的研究还有待深入。