改进的PSO优化SVM的病理图像分类算法

董斌，王云涛，贾立男，王娅南

(1.河北大学附属医院 发展规划办公室，河北 保定 071002；2.河北大学 电子信息工程学院，河北 保定 071002；3.河北大学附属医院 病理科，河北 保定 071002)

医学图像的分类检测方法目前主要为自适应强、学习能力强的机器学习算法中的分类器算法.然而，单个分类器在处理高维度图像时识别率较低，多个分类器一起使用又会增加计算的复杂度.因此，分类器的优化问题成为了很多图像处理领域的一个热点问题[1].如何获得理想状态的目标极值就是最优化问题，而这个目标的实现则是在满足约束条件的可行域上找到的，并且不需要对所有可能的结果进行检验[2].

优化算法因其简单易用的特点获得许多学者的关注[3].优化算法中最常用的是群智能优化算法，该算法的主要思想是模仿自然界中的生物种群行为.粒子群算法是群智能优化算法里面最新被提出的，该算法简单易实现，收敛速度快，并且在算法的性能和分析上取得了众多研究成果[4],因此被广泛应用于优化问题[5].

本文通过提出自适应寻优函数来改进PSO(particle swarm optimization)优化算法，将改进的PSO算法应用于SVM(support vector machine)分类器，进行医学图像的分类检测，从而提高SVM的分类准确率.

1 优化算法背景

近年来，智能优化算法主要有：遗传算法[6]、人工神经网络算法、模拟退火算法[7]、蚂蚁群优化算法[8]和粒子群优化算法[9].

粒子群优化算法的原理简单易使用，且应用相较于其他算法更为广泛.因此，本文选择对粒子群算法进行改进，并通过使用改进的粒子群算法来优化分类器从而提高分类器分类结果的准确率.经典粒子群算法的缺点主要体现在2个方面：1)因为算法收敛速度快，粒子寻优存在趋同性，致使算法极易步入局部极小；2)算法在寻优后期出现严重的震荡现象，从而对算法后期的收敛速度产生较大影响[10].针对算法所存在的问题，大部分学者的研究主要集中在分析算法中的粒子的运动轨迹和算法的收敛性[11]2个方面.粒子的运动轨迹相关的研究主要有：Clerc等[12]研究了粒子群算法中粒子的运动情况并进行了分析说明；Eberhart等[13]在粒子运动的参数选取上做了大量的实验并提出了参数值的给定数值；Suganthan等[14]提出在迭代的过程中,2个学习因子线性递减的方式可以改进粒子运动的轨迹；Ratnaweera等[15]则提出学习因子c1线性递减、学习因子c2线性递增的方法；在文献[16]中的定理则提出粒子群算法可以不用考虑粒子的速率.算法的收敛性的相关研究主要有：Shi等[17]首次发表了惯性权重线性递减概念的改进方法；文献[18]针对惯性权重的调整提出了迭代次数增加而惯性权重减小的方法，以此实现算法收敛性能的改进；文献[19]给出了随机惯性权重策略；文献[20]提出了新的改善惯性权重的方式；文献[21]在标准粒子群算法中加入了收敛因子k来改进算法的收敛性.

粒子群算法[22]的混合应用在函数的优化[23-24]、神经网络的权值训练[25-26]、智能控制[27-28]、工程应用[29]和电力系统的优化[30-31]等方面较为广泛.例如，在神经网络的训练中，有研究人员将遗传算法和粒子群算法结合对神经网络进行权值训练[32]，使该算法简便好用[33].医学图像的分类检测结果能够直接影响医生的临床诊断和病人的后续治疗，所以智能化的分类检测算法是非常必要的.分类器的设计和优化成为了提高分类器性能的主要方法.例如，研究人员通过使用PSO算法来优化SVM参数从而提高SVM的性能，进而大大提高了病理图像分析处理结果的精度[34].

2 经典PSO算法与改进PSO算法

2.1 经典粒子群算法概述

经典粒子群算法是在对动物集群活动的行为观察的基础上，利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解.

经典粒子群算法的速度位置更新公式如下：

假设搜索范围维度为d,粒子个数为m，其中第i个粒子在时刻t的速度、位置更新公式为

(1)

(2)

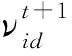
2.2 基于自适应原则下的改进粒子群优化算法

适应性原则，即当改变行为模式带来的回报是值得的时候，群体应该改变其行为模式.基于此原则，改进的粒子群算法中增加了位置权重和加强粒子之间相关性的函数，并将不再考虑粒子速度的影响.

首先，根据适应性原则，在现有PSO算法的位置更新公式的基础上加入了位置权重w，使得粒子群在搜索最优位置的过程中，能够更好地判断最优位置.其次，引入了函数s*(maxt-t)/maxt，其中，系数s为相关性系数，加强粒子与粒子群位置之间的相关性.最后，去掉了速度更新公式，根据相关研究，由于粒子的速度只是代表了粒子移动的快慢程度，并不代表粒子能够有效趋近最优解位置，所以防止粒子偏离正确的方向，影响后期收敛速度，本文将不再考虑速度的影响.

改进的粒子群算法的计算公式表示为

(3)

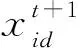
公式(3)中新引入的函数s*(maxt-t)/maxt是为了增强粒子间的相关性，其中s是范围为[0,2]的相关性系数，maxt表示最大迭代次数，t为当前迭代次数，xbest表示群体的位置最优值.

3 5种算法分类检测病理图像实验

通过对腺癌病理图像进行分类实验，验证本文算法的有效性.实验中用于进行分类检测的特征是HOG特征.本章将通过比较5种算法的分类结果来验证算法的性能.这5种算法分别是：1)没有使用粒子群算法优化的SVM分类算法；2)经过经典粒子群算法优化的SVM分类算法；3)引入了惯性权重w的PSO优化SVM的分类算法；4)引入了收敛因子k的PSO优化SVM的分类算法；5)本文提出的改进的粒子群算法优化的SVM分类算法.这5种算法均在MATLAB下实现.

3.1 实验环境及病理图像来源

本实验的算法是在MATLAB R2016a版本下实现的.实验测试数据是500张随机在网络中选取的经由专家诊断的腺癌病理图像，每张图像的像素为128*64.在实验过程中，将图像分为训练集、测试集和验证集3个部分，其中，训练集和测试集分别由200张图像组成，并根据标本的性质分为100张正样本和100张负样本.训练集和测试集将用于对SVM分类器进行初始化的训练和测试，其余的100张病理图像将作为验证集用于验证不同算法的分类有效性.

3.2 实验参数的设定

改进的PSO算法以及经典PSO算法的2个学习因子c1和c2根据前人经验分别初始化为1.7和1.5.改进PSO算法中引入的迭代寻优函数中的系数s，取值范围设定为[0,2].

3.3 本文改进算法的实现

改进的PSO优化SVM参数算法，主要是在位置更新公式中加入了原来公式中没有的位置权重以及用于增强粒子之间相关度的函数公式，然后去掉了速度更新公式.在运行算法时，首先通过改进的PSO算法优化SVM的参数c和g；然后建立SVM并进行训练；最后训练好的SVM对验证集里的图像进行分类验证，得到分类结果.

本文改进粒子群优化SVM算法的程序步骤如下.

Step1：首先对输入的病理图像进行处理，将输入的图像转换为灰度图像，并归一化处理.

Step2：然后对训练集以及测试集里面的每一幅图像进行HOG特征提取，HOG特征提取公式为

(4)

其中，s(x,y)是像素点(x,y)的特征信息，Gx和Gy是像素点(x,y)在水平和垂直方向的特征信息.

Step3：特征提取结束后，建立所有训练图像标签

Trainlabels=imdsTrain.labels，

(5)

Trainlabels表示建立的训练标签，imdsTrain.labels表示训练图像建立的标签名.

Step4：改进的PSO寻优算法优化SVM参数c和g，进行数据训练完成SVM模型建立以及训练，PSO优化公式为

(6)

Step5：测试并计算准确率，准确率公式为

Accuracy∶ACC=((PT+NT)/Dsamples)×100%，

(7)

其中，PT表示正样本正确检出数，NT表示负样本正确检出数.Dsamples表示样本图像数目.

Step6：验证集验证分类结果，1表示分类正确，0表示分类错误

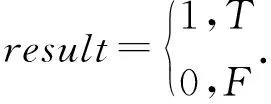
(8)

4 结果及分析

4.1 改进粒子群算法实验结果

图1表示分别使用测试集200张图像、验证集100张图像进行检验的分类结果.图1表示的是改进的PSO优化SVM分类算法分别在测试集和验证集上的分类检测结果.横坐标表示分类结果，1表示正确检出数，0表示误检数；纵坐标表示样本数量.本文算法在测试集中的检出数为197张，误检数为3张，分类准确率为98.5%；验证集中的检出数为99张，误检数为1张，分类准确率为99%.

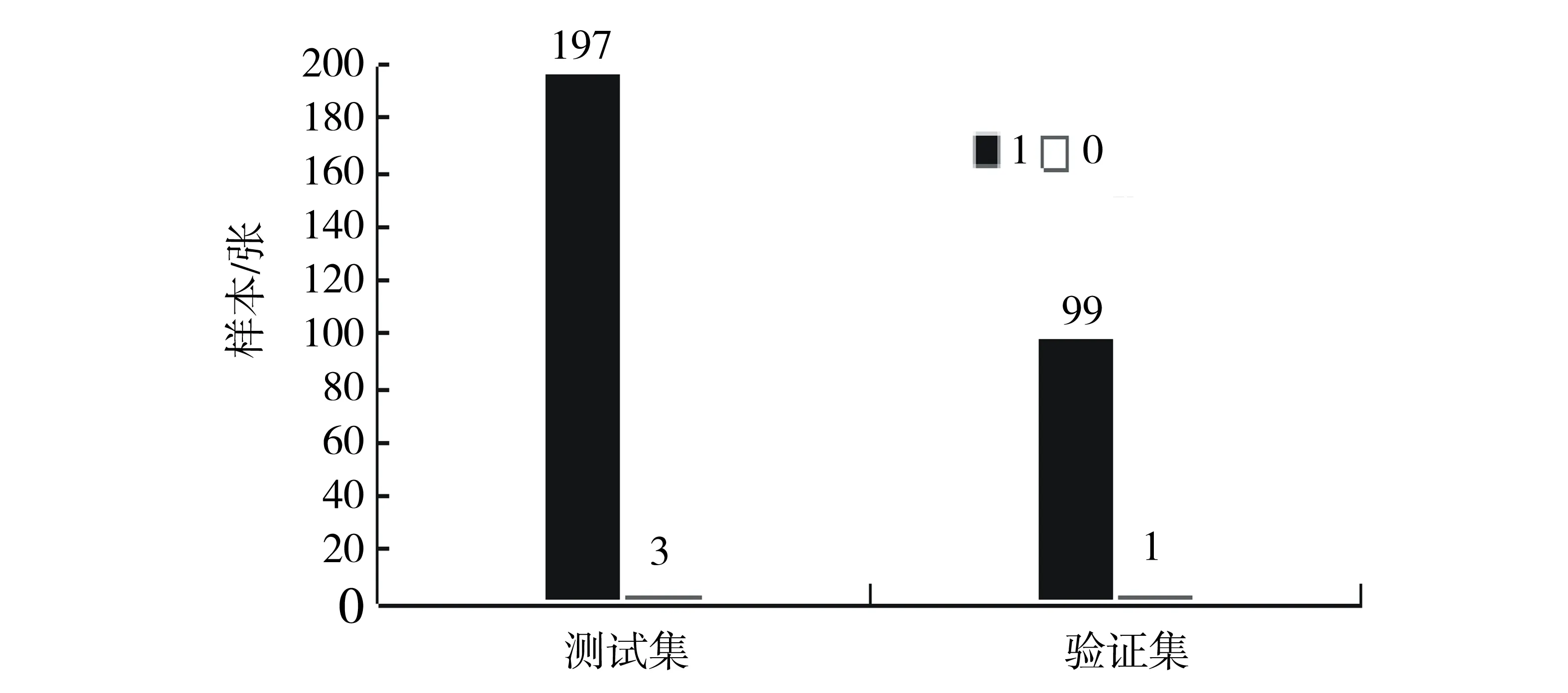
图1 改进粒子群优化算法优化SVM分类器的分类结果Fig.1 Classification results of SVM classifiers optimized by improved particle swarm optimization algorithm

由于改进的粒子群算法不再考虑速度对粒子运动的影响，所以不存在算法后期由于粒子速度的影响，导致微粒失去探索新区域的能力.此外，粒子的个体以及群体的综合位置信息通过自适应迭代寻优函数的处理，能够使得粒子搜索到的最优解更加可靠，所以验证效果较好.

4.2 引入惯性权重的PSO优化SVM的分类算法的实验结果

本节中PSO优化算法的改进在速度更新公式中引入了惯性权重w，实验结果为图2所示.

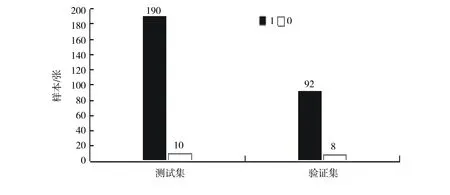
图2 带有惯性权重的粒子群优化算法优化SVM分类器的分类结果Fig.2 Classification results of SVM classifiers optimized by particle swarm optimization algorithm with inertial weight

图2为该算法分别在测试集和验证集上的分类结果，横坐标表示分类结果，1和0分别表示检出数和误检数；纵坐标表示测试集样本数量.该算法在测试集中的检出数为190张，误检数为10张，分类准确率为95%；在验证集中的检出数为92张，误检数为8张，分类准确率为92%.算法引入了惯性权重，提高了PSO性能，由于粒子后期震荡的出现会导致分类出现误差的情况.

4.3 引入收敛因子的PSO优化的SVM分类算法的实验结果

本节中PSO算法的改进是在速度更新公式中引入了收敛因子k，实验结果为图3所示.图3为该算法分别在测试集和验证集上的分类结果，横坐标表示分类结果，1 和0分别表示检出数和误检数；纵坐标表示测试集样本数量.该算法在测试集中的检出数为170张，误检数为30张，分类准确率为85%；在验证集中的检出数83张，误检数为17张，分类准确率为83%.算法引入了收敛因子，加快了粒子收敛速度的同时但是由于粒子速度容易陷入局部极小值，出现局部最优的情况，所以分类结果较差.

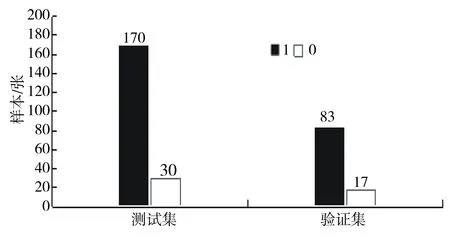
图3 带有收敛因子的粒子群优化算法优化SVM分类器的分类结果Fig.3 Classification results of SVM classifiers optimized by Particle swarm optimization algorithm with convergence factor on test set and verification set

4.4 经过经典PSO优化的SVM分类算法的实验结果

经典PSO优化的SVM算法在测试集和验证集上的分类结果为图4所示.图4为经典PSO优化SVM算法分别在测试集和验证集上的分类结果，横坐标表示分类结果，1和0分别表示检出数和误检数；纵坐标表示测试集样本数量.该算法在测试集中的检出数为166张，误检数为34张，分类准确率为83%；在验证集中的检出数为75张，误检数为25张，分类准确率为75%.

经典粒子群算法中，粒子在解空间中进行搜索时，由于位置更新公式中的速度这一属性的影响，在寻优后期出现了惯性权值过小而不能探索新领域的问题，从而导致算法陷入局部最优.图4说明这种局部最优的问题严重影响了粒子最优位置的寻找，所以在进行优化SVM分类检测时效果欠佳.

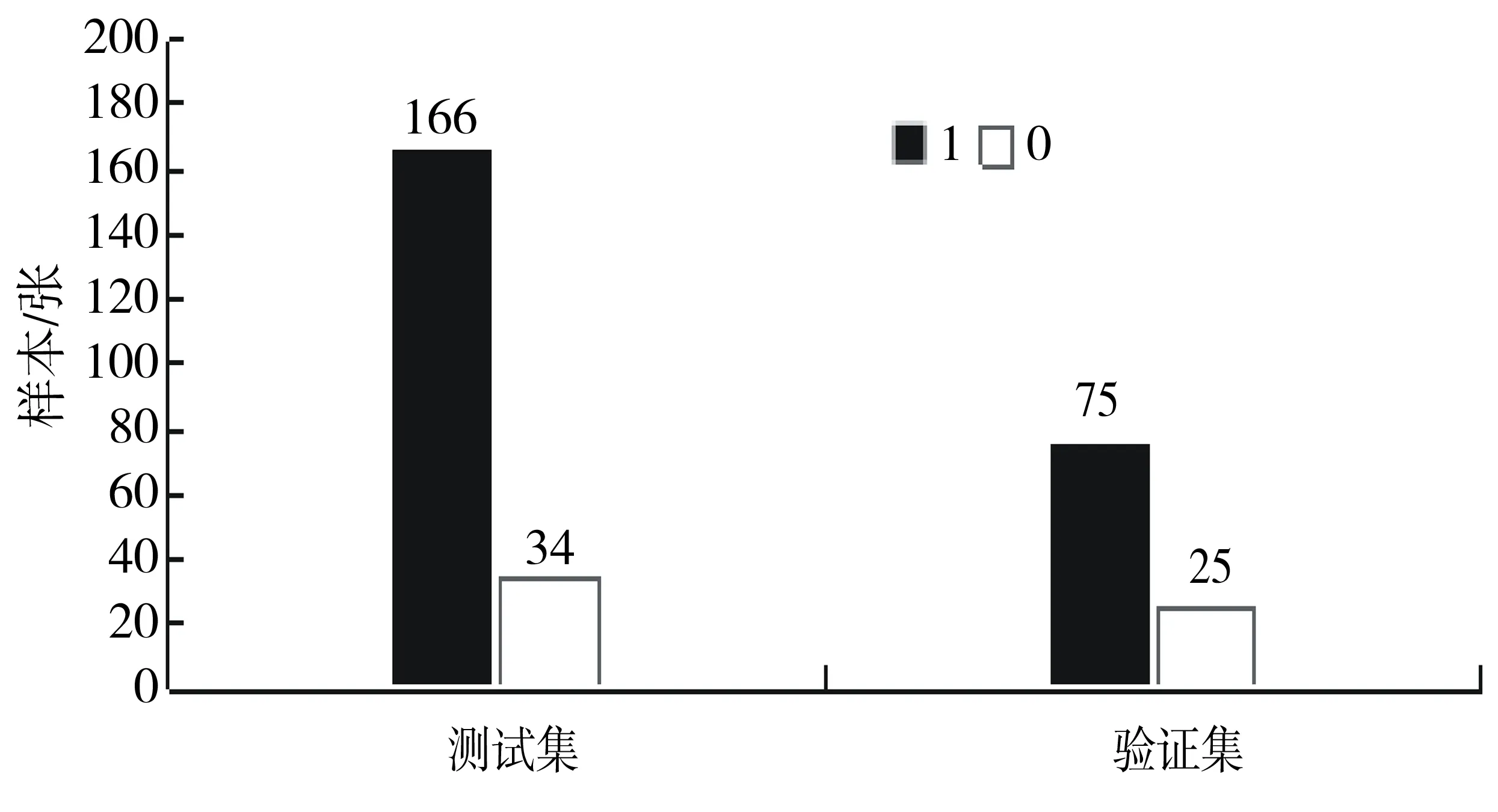
图4 经典粒子群优化算法优化SVM分类器的分类结果Fig.4 Classification results of SVM classifiers optimized by classical particle swarm optimization algorithm on test set and validation set

4.5 无PSO优化的SVM算法的实验结果

使用原始的SVM分类算法来进行分类检测.图5为无PSO优化的SVM分类器的分类结果.

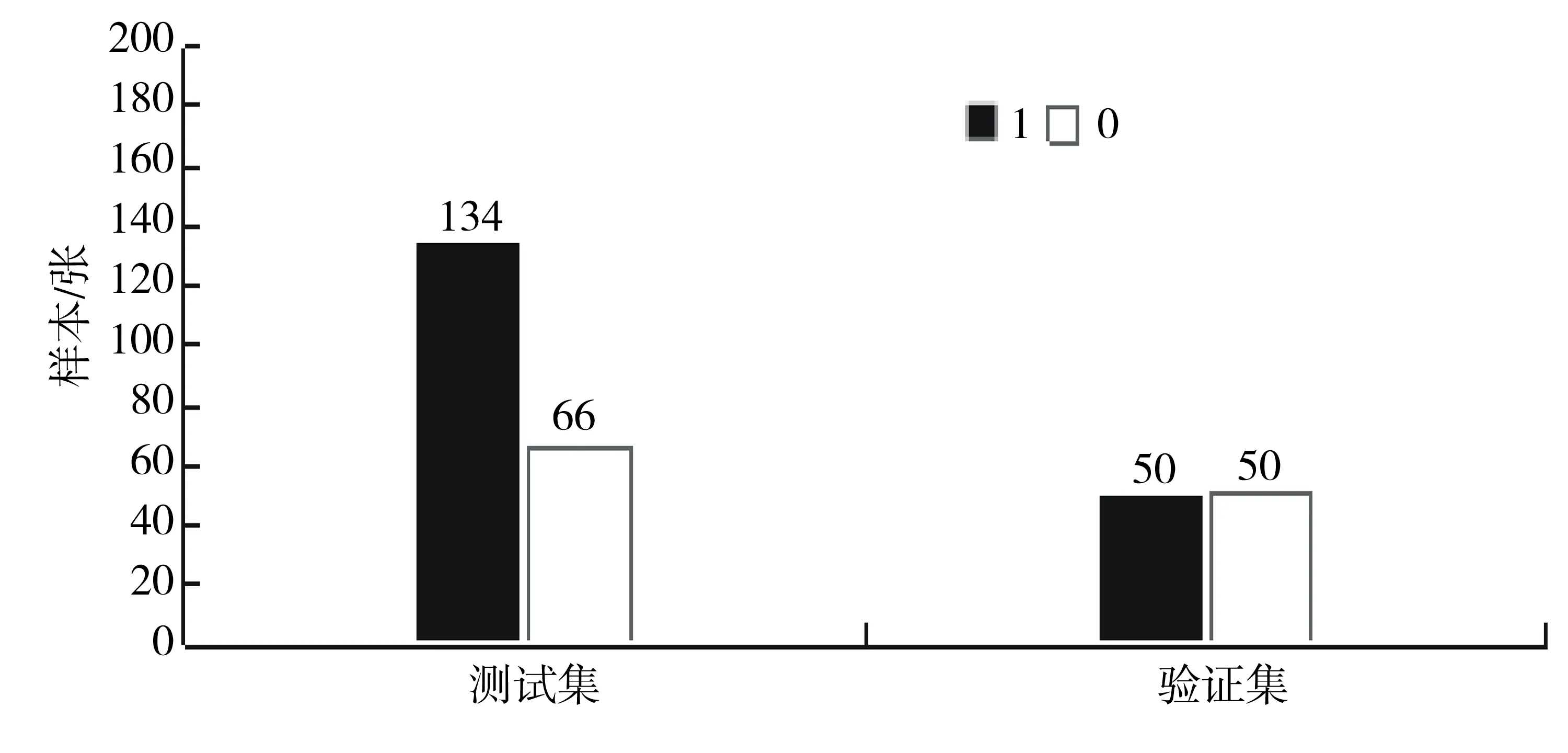
图5 无优化的SVM分类器的分类结果Fig.5 Classification results of non-optimized SVM classifiers on test set and validation set

图5表示无PSO优化的SVM算法分别在测试集和验证集上的分类结果，横坐标表示分类结果，1和0分别表示检出数和误检数；纵坐标表示样本数量.在测试集中的检出数为134张，误检数为66张，分类准确率为67%；在验证集中的检出数为50张，误检数为50张，无PSO优化的算法在验证集上的分类准确率为50%.在没有使用PSO算法优化SVM参数的情况下，算法的分类检测结果较差.

4.6 各个算法分类准确率的分析

前面提到的各个算法的分类结果，本文定义准确率为正确检测出的图像数目占所有图像数目的百分比，其中测试集的分类准确率的计算公式为

Accuracy:ACC=((PT+NT)/Dsamples)×100%.

(9)

公式(9)为计算准确率的公式，其中PT表示正样本正确检出数，NT表示负样本正确检出数.Dsamples表示测试集里面的样本图像数目.

验证集的分类准确率为

Accuracy:ACC=((PT+NT)/Dsamples)×100%，

(10)

其中，PT表示验证集中正样本正确分类的图像数，NT表示验证集中负样本正确分类的图像数，Dsamples表示验证集样本总数.

5种算法的实验结果对比如表1所示.

表1 5种算法结果数据对比Tab.1 Comparison of the results of the five algorithms

根据表1所示，5种算法中本文算法在测试集和验证集上的分类准确率明显要较高于其他算法.表1中每个算法在测试集上和验证集上的分类准确率的对比，表明了：1)测试集的分类结果表明，本文算法引入位置权重和相关度函数能够考虑到粒子当前时刻的个体位置信息和粒子整体的最优位置信息来更新粒子的位置，这种方法是可行的.2)验证集的分类结果表明，这几种算法得到的SVM分类器在进行实际操作时本文算法得到的SVM分类器分类性能较好，进一步表明分类器的优化是提高分类器分类性能的有效方式.

本文所提出的方法通过不断改进的粒子群算法使得函数寻优跳出了局部最优值，寻找到了位置最优解，从而使得分类检测结果得到提高.实验结果表明本文提出的改进的粒子群算法在图像分类检测的精确度上得到了较好的效果.

5 讨论

针对粒子群算法在易陷入局部最优解、后期震荡等问题，采用在位置公示中引入了粒子的惯性权重以及表示粒子之间相关度的公式的方法，改进了PSO算法，避免了局部最优的出现，有效提高了算法的稳定性和可靠性，减少了后期易陷入局部最优的情况.通过使用腺癌病理图像进行实验证明本文算法在分类检测病理图像上是实用有效的.下一步将继续在参数优化和分类器检测方面展开研究，从多样本分类检测和多算法结合角度研究算法的性能.本文给出了优化支持向量机参数的改进PSO算法，在不考虑速度因素的影响下，使得PSO优化性能得到提升，并且支持向量机分类检测的准确率提高.