机载雷达数据融合效能评估

陈福年

(中国电子科技集团公司第三十八研究所,安徽 合肥 230088)

0 引 言

随着现代机载雷达的发展，机载雷达装备越来越丰富，功能也更全面。但是受到飞机运动平台的限制，机载雷达的定位精度较差，在现有的雷达装备下，仅仅依靠单个机载雷达无法实现对目标的高精度探测。为了提高机载雷达的探测精度，充分利用机载雷达的运动平台优势，本文介绍了运动平台下的数据融合方法，并对融合精度提出了评估方法。

机载雷达由于其运动灵活的优势，被广泛用于各种战场，能够快速侦察战场中的各个角落。但是由于机载雷达受限于载机平台，一方面是由于雷达功率和雷达孔径尺寸都受限，另一方面是由于目前国内惯性导航技术瓶颈，使得机载雷达的探测精度受限。文中采用双机协同探测进行数据融合，可以极大地提高目标定位精度。典型场景为2部机载雷达通过战场数据链互相通信，完成探测情报的数据共享，每一部雷达各自进行探测数据融合，通过双机数据的融合提高定位精度，最后对双机融合结果进行了仿真评估。文献[1]对分布式协同定位的精度进行分析，但没分析载机在运动过程中由于位置变化对协同定位精度的影响；文献[2]对定位精度的计算过程分析得详细入微，但是缺少雷达站不同方位分布情况下定位精度的差异；文献[3]对组网数据融合过程中的误差源进行细致的分析，但没有给出有效提高组网融合精度的方法。

本文针对双机探测时的位置不同，主要对融合后定位精度的影响进行了分析，通过定位精度的变化可以评估双机协同带来的精度提升。从目前文献对数据融合精度的研究现状来看，大多研究更关注融合过程中的数值计算方法和计算过程中的误差，而对运动平台的多雷达融合精度影响的研究较少。因此，文中针对机载雷达协同探测时，载机位置运动对探测的融合精度进行了分析和推导，并进行仿真验证，对运动平台的融合定位精度进行评价。文中分析了理想情况下，双机协同探测时数据融合后雷达探测距离、方位精度的计算方法。

1 系统模型

雷达量测的系统误差模型如图1所示，量测距离为r，量测方位角为θ。雷达量测误差服从高斯分布，量测距离标准差为σr，量测方位标准差为σθ。量测距离服从高斯分布(0，σr)，量测方位服从高斯分布(0，σθ)。雷达的量测误差通常情况下存在距离误差小而方位误差偏大的特点，量测误差示意图如图1所示。

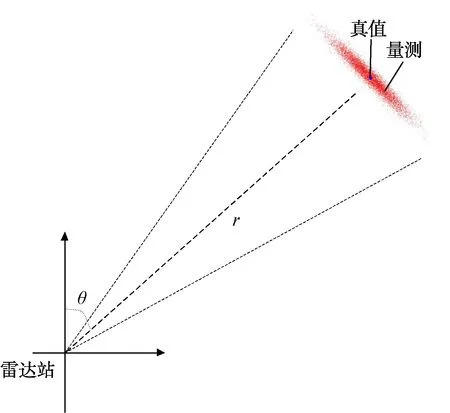
图1 雷达量测误差仿真模型

仿真场景如图2所示，机载雷达B和C同时对目标A进行探测，雷达B和C将探测后的结果通过数据链共享探测数据，然后各自进行数据融合。我们假设机载雷达为两坐标雷达，只能测得距离和方位，不考虑高度影响。假设机载雷达B探测到目标A的距离和方位为(r1,θ1)，机载雷达C探测到目标A的距离和方位为(r2,θ2)。这里假设系统可以做到时间精准同步，假设机载雷达B的量测距离均方根误差为σr1，方位均方根误差为σθ1；机载雷达C的量测距离均方根误差为σr2，方位均方根误差为σθ2。

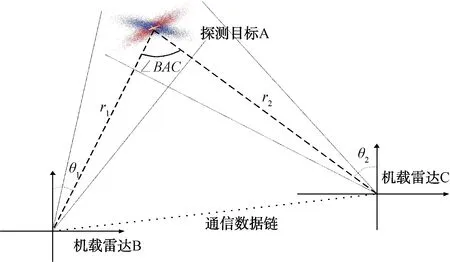
图2 双机协同探测场景

由于机载雷达B和C的运动，当双机夹角∠BAC发生变化时，融合结果会发生变化，AB、AC的距离不同，融合结果也有区别，下面针对双机的位置变化分析数据融合性能。

2 数据融合方法

数据融合处理是对多传感器上报的量测点迹数据进行量测融合，融合完成后进行雷达目标跟踪，本文只讨论在卡尔曼滤波前进行量测融合后的精度变化情况。

量测融合方法可分为两大类：量测合并(即数据压缩)方法和串行处理方法。量测合并方法是指将多个传感器在统一的时间轴上对同一目标的量测数据进行数据合并，将多个探测数据压缩成1个数据。这种方法适合于天线同步扫描雷达，如一、二次雷达的综合；而对于非同步采样的多传感器融合，如多部雷达数据的融合，则可以采用时间校准和目标状态平移的方法，将异步数据变换成同步数据后再进行点迹的量测合并处理，最后进行跟踪和滤波处理。

假设不考虑时间同步和状态平移引起的误差，设(r1,θ1)、(r2,θ2)分别为雷达1和雷达2的距离和方位的测量值，对2部雷达的量测值进行合并处理，可采用下式[4]对它们进行点迹合并：

(1)

(2)

上述公式为雷达融合误差计算公式，从上述算式可以看出：估计的结果是各雷达的测量按精度加权；合并后点迹精度有所提高。

量测数据合并在数据融合处理中有着广泛的应用，在通常的雷达融合处理中的处理流程是先接收多部雷达的量测数据，然后对接收的数据进行状态平移和时间对齐，时间对齐以后就可以对量测数据进行数据融合，最后对融合后的量测进行常规的跟踪滤波。本文只对数据融合结果进行分析，数据融合流程如图3所示，不同颜色的圆点表示不同雷达的探测点。

图3 数据融合流程

从图3不难看出，本文的融合处理方法有一个显著特点是先进行量测数据融合，然后进行跟踪滤波处理。在实际情报融合处理系统中，遇到的情况比较复杂，这里不做讨论，下面单独就量测数据的融合精度进行分析。

3 融合精度计算

根据文献[5]中提出的无偏转换的方法，将雷达量测误差无偏转换到直角坐标系下，然后在直角坐标系下采用公式(1)、(2)计算融合后的量测位置，最后再转换到雷达量测极坐标系下计算融合误差，最终通过融合精度比较，评估融合效果。

步骤如下：

(1) 进行量测预处理，对量测进行转换，计算直角坐标系下量测误差的均方差。

(3)

(2) 展开公式，将2个雷达的量测代入式(3)得到直角坐标系下的量测误差的均方差：

(4)

(5)

(3) 根据公式(1)、(2)计算融合后的直角坐标系下的量测值xF，yF：

(6)

4 仿真实验及评估

假设2部机载雷达都能探测到目标，2部机载雷达与目标距离在50～350 km之间，两机夹角在0°～180°之间变化，场景如图2所示。单部雷达的测角精度0.25°，测距精度60 m。基于以上条件，主要分析两机运动过程中的融合精度的变化。理想情况下，采用上节中数据合并方法对量测数据进行融合，通过蒙特卡洛仿真方法对融合处理后的定位精度进行评估。

距离融合精度随夹角和探测距离的变化关系如图4(a)所示。根据仿真结果可以看到，融合后，当双机夹角较小的情况下，距离精度明显提高，计算方法参考第3节中融合方法；当双机夹角接近90°时，由于雷达方位误差影响，距离精度下降，且目标距离越远距离精度下降越大。融合后的方位精度大幅提高，仿真结果与理论相符。

方位融合精度根据夹角和探测距离的变化关系如图4(b)所示，根据仿真结果可以看到融合后当双机夹角较小的情况下，方位精度明显提高，计算方法参考第3节中公式；当双机夹角接近90°时，由于雷达距离误差相比方位误差较小，方位精度有更明显的提升，通过较高的距离精度弥补雷达方位精度较差的影响。融合后的目标探测距离精度大幅提高，仿真结果与理论相符。

图4 双机协同距离方位精度分析

5 结束语

通过实验表明，采用双机协同或多机协同的方式进行数据融合，能够有效提升雷达探测精度，可以弥补方位探测误差较大的缺点。实验中采用雷达测距误差60 m，测角误差0.25°的输入精度，经过双机融合后方位精度有明显提升，距离精度可以采用过滤的方式保证距离精度不变，过滤处理后通过图5可以看出双机协同情况，雷达探测精度明显提高，如表1所示。

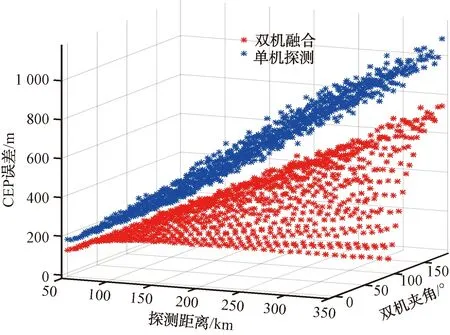
图5 双机协同CEP精度分析

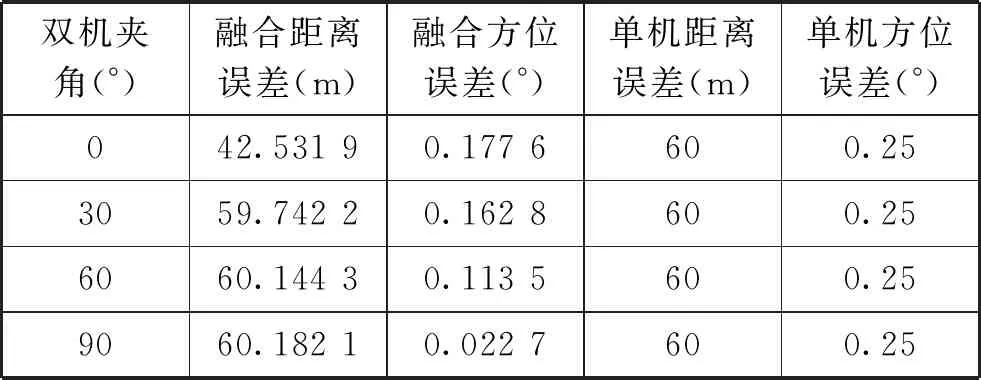
表1 双机融合精度对比