一种舰载RCS测量雷达极化补偿方法

史厚宝，顾 兵

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

0 引 言

舰载雷达截面(RCS)测量雷达，在对目标极化特性进行测量时，如果舰船摇摆，天线极化方向将随之不断发生变化，此时进行极化特性测量则必将导致目标极化特性测量结果错误，因此必须采取极化补偿措施克服舰船摇摆对目标极化测量的影响。传统的方法是采用稳定平台的方式，即将整个测量雷达放在稳定平台上，由稳定平台来克服舰船的摇摆[1]。由于此种稳定方式不仅要克服整个雷达的摇摆，还要克服风阻力对稳定平台的影响，稳定平台不仅体积大、重量重、成本高、适装性差而且控制精度很难做高。本文提出一种通过扭转馈源极化的方式来稳定天线的极化，此种方法是在两轴跟踪雷达的基础上，根据极化变化而单独采用馈源扭极化装置对极化进行补偿的一种方法，此种稳定方式不仅轻巧、灵活、精度高而且不影响雷达的适装性。

1 各坐标系定义

1.1 地理坐标系

地理坐标系定义为y轴指向地理北，x轴指向地理东，z轴由右手定理垂直于地理表面向上，具体坐标系规定如图1所示。

图1 大地坐标系示意图

1.2 甲板坐标系

甲板坐标系的定义为y′轴指向舰艏，x′轴指向右舷，z′轴由右手定理获得垂直于x′轴、y′轴构成的平面，具体坐标系规定如图2所示。

图2 甲板坐标系示意图

1.3 天线坐标系

天线坐标系的定义为y″轴指向天线法向，x″轴为天线所在平面指向右侧，z″轴可根据右手定理得到在天线所在平面指向上，具体坐标系规定如图3所示。

图3 天线坐标系示意图

1.4 各坐标系之间的关系

甲板坐标系与地理坐标系之间的关系如图4所示，舰船的航向、纵摇、横摇定义符合卡尔丹环架结构[2]，航向H(为舰艏线在xoy平面内的投影与y轴之间的夹角，右偏为正)，横摇p(舰艏线与其在xoy平面内的投影的夹角，上仰为正)，横摇R(右舷与其在xoy平面内投影的夹角，下俯为正)。

图4 甲板坐标系与地理坐标系之间关系示意图

天线坐标系与甲板坐标系之间的关系如图5所示，天线相对甲板坐标系的方位为A(天线法向轴y′在xy平面内投影与舰艏y轴的夹角右偏为正)，俯仰角为E(天线法向轴y′与xy平面之间的夹角，上仰为正)，横倾为R(x′z′面绕y′轴旋转的角度)。

图5 天线标系与甲板坐标系之间关系示意图

综合上述坐标系之间的关系可知，甲板坐标系与地理坐标系可通过导航信息实现相互转换，天线坐标系和甲板坐标系可以通过天线相对甲板的姿态信息实现转换，那么天线坐标系与地理坐标系之间可以甲板坐标系为媒介实现相互转换。

2 极化补偿角数学表示

天线极化方向，如图6所示，垂直极化时平行于z″轴，水平极化时平行于x″轴，因此对于极化的变化可以看成是天线坐标轴的变化。因此只要知道天线坐标轴相对于地理坐标的变化便可以获得极化相对地理坐标的变化。

图6 天线极化方向示意图

为了获得天线坐标相对地理坐标的状态，需以甲板坐标系为媒介，将舰船纵横摇转换为天线的纵横摇。设舰船的航向为H，纵摇为P、横滚为R；天线相对于舰船的姿态方位为A，俯仰为E、横倾为B，具体见上图，那么可以通过坐标旋转变换将舰船的纵横摇转换为天线的纵横摇，转换关系如下：

(1)

式中：R′、P′、H′分别为天线相对大地的横摇、纵摇横航向；MB为横滚旋转矩阵；ME为仰角旋转矩阵；MA为方位旋转矩阵。

其表达式分别为：

(2)

(3)

(4)

则：

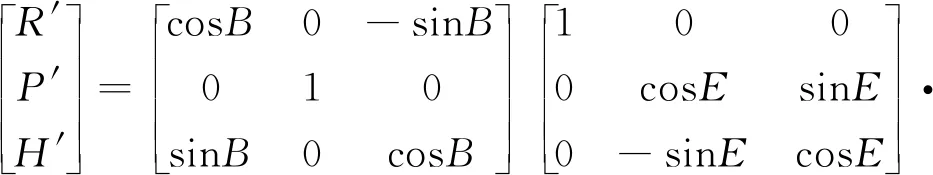
(5)

由式(3)可得：

R′=R(cosAcosB+sinAsinEsinB)-P·(cosBsinA-cosAsinEsinB)-HcosEsinB

(6)

横滚B是天线相对甲板平面的安装横滚角，设备与甲板安装为刚性连接，通常情况下B=0，则：

R′=RcosA-PsinA

(7)

由式(7)可知，R′与纵摇P、横摇R、天线相对舰船的方位A有关。一般情况下，纵摇P、横摇R可以通过导航信息获取；天线相对舰船的方位A与目标的位置有关，因此需根据目标位置获取天线相对舰船的方位A。

这里主要讨论角度上的转换关系，为方便讨论设目标在大地坐标下的角度分别为：方位φ，俯仰为θ，长度为单位长度，则目标可以表示为：

(8)

由坐标系旋转变换关系[3-5]，目标在甲板坐标系下的坐标可表示为：

(9)

式中：x′、y′、z′为甲板坐标系下的坐标；Rt、Pt、Ht为旋转变换矩阵：

(10)

(11)

(12)

则：

(13)

则：

(14)

由式(14)便可得到天线相对甲板的方位A，将A代入式(7)便可获得实时的纵横摇状态下跟踪此目标时天线极化的变化。

3 仿真与讨论

(1) 极化补偿范围

舰船摇摆根据海情一般有一定的范围，例如5级海情下，舰船的横摇≤10°，纵摇≤7°，设纵摇P=7°，横摇R分别为-10°、-5°、0°、5°、10°时，天线相对舰船360°旋转时，极化扭转角如图7所示。

(2) 测量目标时的极化补偿

在对目标进行测量时，雷达稳定跟踪目标，假设目标位置不变，讨论纵横摇及航向发生变化时的极化变化情况。

(a) 目标不变，不同航向、不同纵摇下，极化随横摇变化

从图8、图9仿真结果可以看出,当目标固定在正北，航向也在正北位置时，测量雷达稳定跟踪目标则其也指向正北，此时极化变化与舰船横摇线性变化，纵摇变化影响极小。在保持以上条件不变、将航向调转90°后，此时极化变化与舰船纵摇同步变化，舰船横摇基本没有影响。上述仿真结果和实际情况吻合。

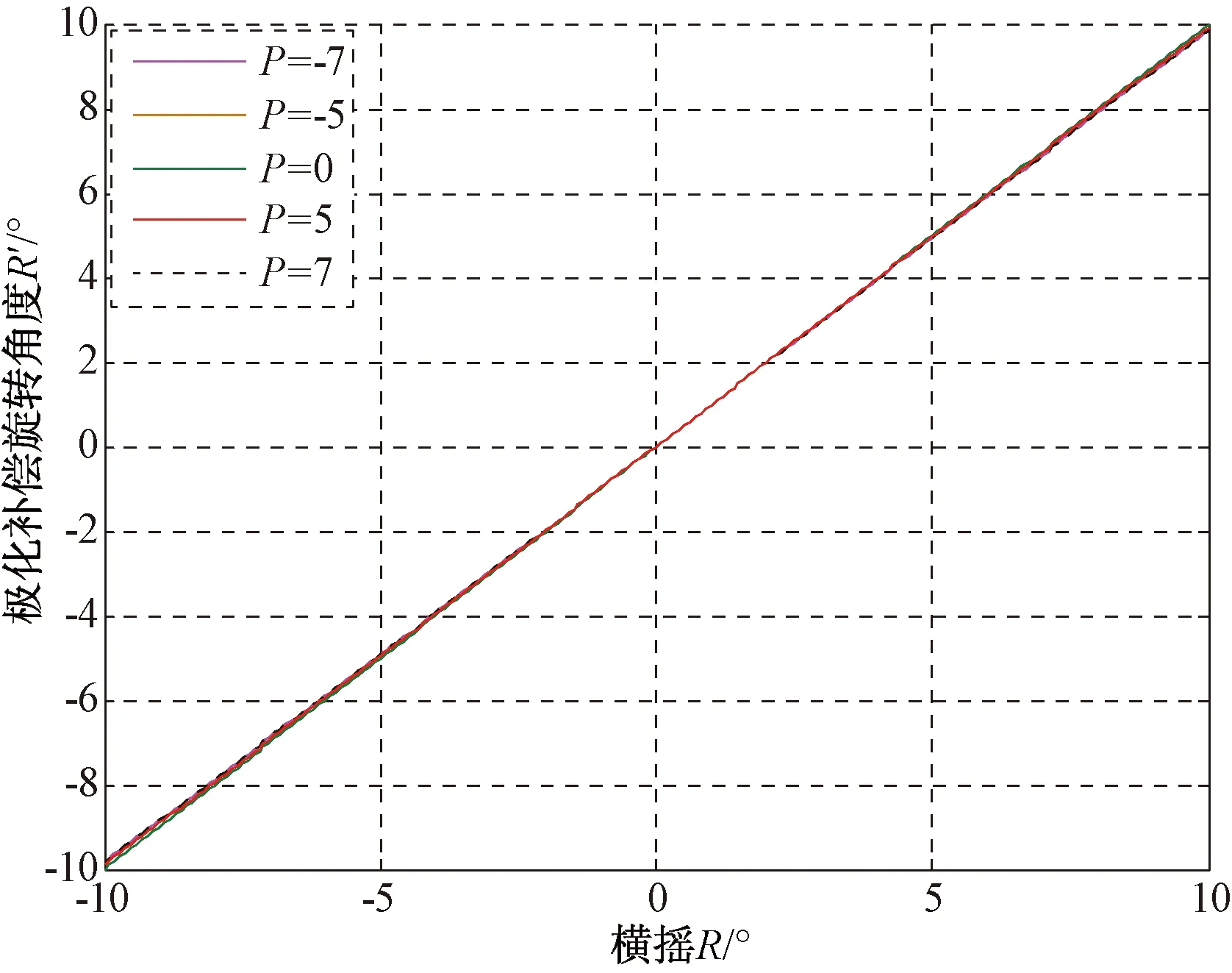
图8 目标方位0°，俯仰0°，航向0°，不同纵摇下极化随横摇变化

图9 目标方位0°，俯仰0°，航向90°，不同纵摇下极化随横摇变化

(b) 目标不变，纵横摇固定，极化随航向变化

从图10、图11仿真结果可以看出,当目标固定在正北、纵摇为0°时，不同横摇下，极化补偿角随航向成余弦变化；在航向90°及180°时即雷达垂直舰船航向时，舰船横摇不影响极化补偿角变化。保持横摇为0°，不同纵摇下，极化补偿角随航向正弦变化；在航向0°(360°)及180°时即雷达平行于舰船航向时，舰船纵摇不影响极化补偿角变化。上述仿真结果和实际情况吻合。

图10 目标方位0°，俯仰0°，舰船纵摇0°，不同横摇下极化随航向变化

图11 目标方位0°，俯仰0°，舰船横摇0°，不同纵摇下极化随航向变化

4 结束语

本文提出一种通过扭转馈源极化的方式来稳定天线极化的方法，对极化补偿角进行了理论推导，同时对结果进行了仿真验证，从仿真计算结果看，本文所采用方式与实际情况吻合。本文结果可用于指导针状波束反射面类测量雷达的极化稳定。