基于雷达辐射源特征的离线情报分析软件设计

陈家瑞，赵 莉，柴 恒

(中国船舶重工集团公司第七二三研究所，江苏 扬州 225101)

1 概 述

离线情报分析软件可以完成谱分析、脉冲参数测量、脉内分析、信号分选、图形显式等功能。并且为了方便用户的人工分析，图形显式可以自助伸缩，在图形上可以通过选点进行辅助测量。离线情报分析软件的组成如图1所示[1]。

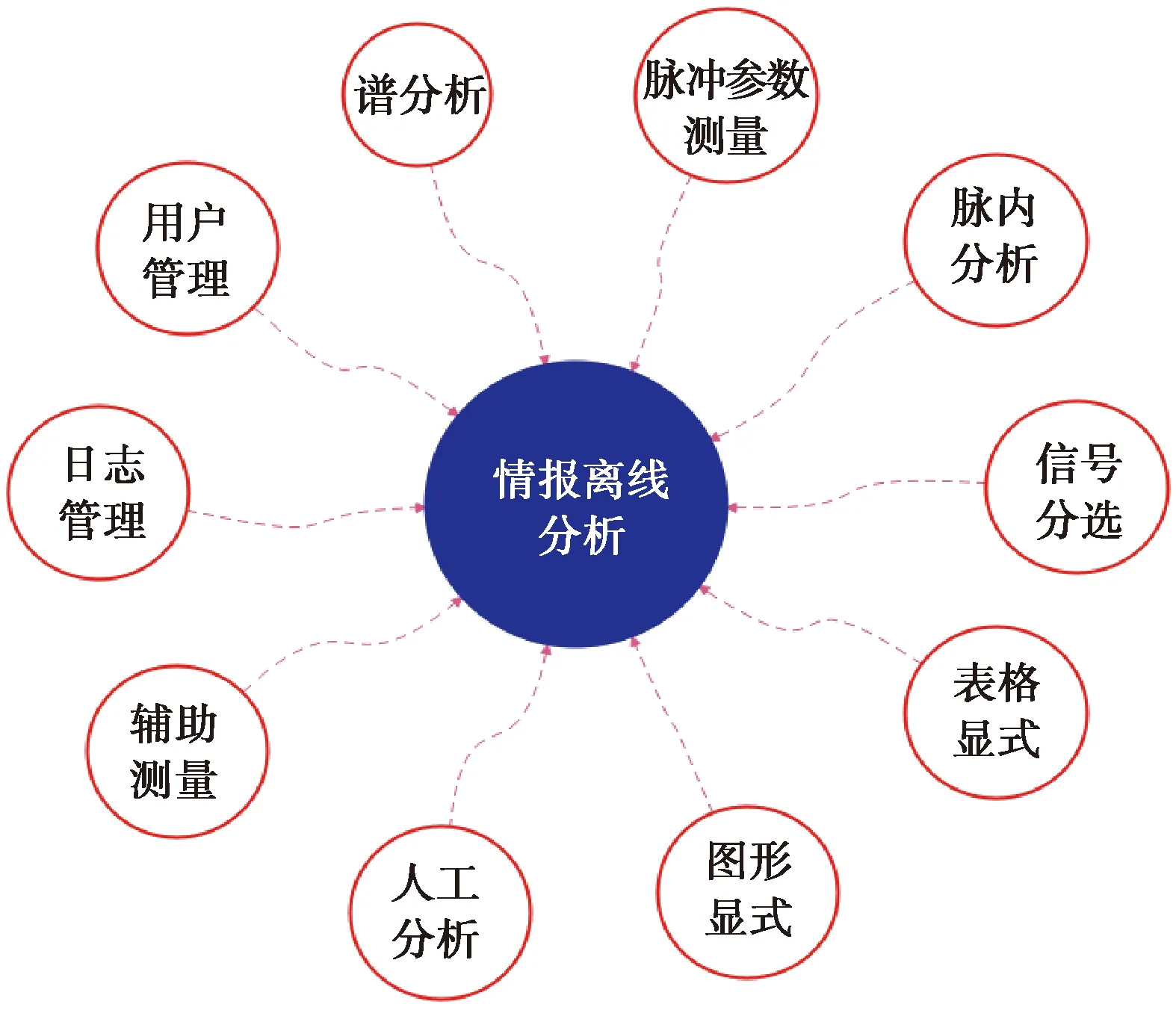
图1 离线情报分析软件

离线情报分析软件具有参数测量精度高、提供广泛测量和分析功能、具备多种直观的显示方式、支持人工参与辅助分析的功能，并具备多文件批处理功能，提高数据分析的效率。在信号脉内测量分析时，采用了信号盲分离技术、信号自适应处理技术、改进Kay瞬时频率估计技术、超窄码元信号识别技术、模糊决策树判决技术等，提高信号分析的精度和准确度。为了对脉间参数测量进行分析，在成熟的累积直方图(CDIF)、序列直方图(SDIF)和时间序列确认方法的基础上，引入了数据挖掘(Data Mining)的GSP(generalized sequential pattern)算法对雷达信号知识进行挖掘，提高信号脉间分析方法对信号的适应性。离线情报分析软件面临着大数据量的问题，因此必须对算法进行加速；通过采用MKL库、OpenMP技术、数据分析并行化技术显著提高情报分析软件的效率。离线情报分析软件的分层架构图如图2所示[2-4]。

图2 离线情报分析软件分层架构图

离线情报分析软件的分析流程如图3所示。

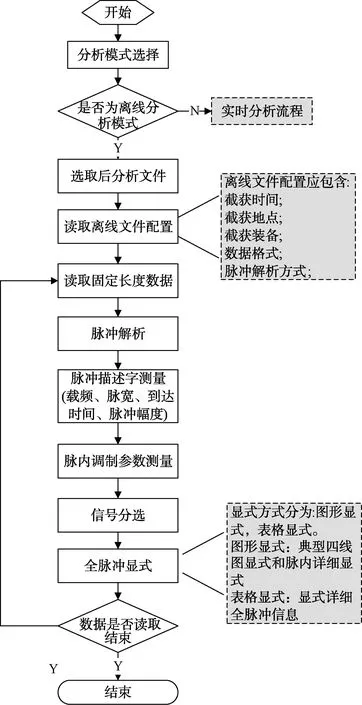
图3 离线情报分析软件分析流程

2 脉内调制参数测量

脉内参数调制测量流程及关键技术如图4所示，各环节作用如下：

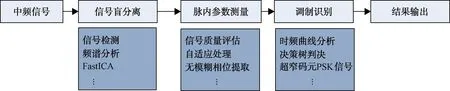
图4 脉内调制参数测量流程及关键技术

(1) 信号盲分离:此模块主要用于分离在时域和频域有混叠的信号，输出分离的中频信号供后续处理。

(2) 脉内参数测量：此模块主要进行信号的参数测量，通过对信号进行质量评估，自适应地分析信号的到达时间、载频、脉宽、功率等关键参数。

(3) 调制识别：利用不同调制类型时频特征的差异，基于决策树判决技术，根据信号时频曲线等特征进行信号的调制识别功能。

下面重点介绍在脉内参数调制测量中使用的信号盲分离技术、自适应处理技术、无模糊相位提取技术[5-6]。

2.1 信号盲分离技术

信号盲分离技术是在时域和频域均有混叠并且信号的先验信息未知的情况下将时频域混叠的信号进行分离。本系统中采用基于快速独立成分分析(FastICA)盲分离方法，分离流程如图5所示。

图5 信号盲分离流程

(1) 对中频信号进行频谱分析，检测谱峰，计算对应谱峰个数和对应谱峰宽度。

(2) 根据谱峰的位置与宽度，用相应的带通滤波器对各谱峰进行滤波，得到初步分离的信号。

(3) 初步分离的谱峰内如果是单一信号，则已经被分离，直接输出用于后续处理。

(4) 对于初步分离后频域混叠信号，采用FastICA算法进行分离。

(5) 综合输出的单个信号与分离信号，最终实现信号盲分离输出。

2.2 信号自适应处理技术

自适应处理技术主要根据不同的信号质量与特征，自动调整处理方法、处理流程和处理参数等，使其与处理数据的统计分布特征、结果特征相适应，提升系统处理速度与结果的可信度，本系统采用的自适应处理方法如图6所示。

图6 自适应处理流程

(1) 针对分离后的信号首先进行信噪比估计，根据信噪比大小采用不同的处理方法。

(2) 对于信噪比低于一定阈值的信号，采用信噪比增加技术提升信号质量。采用信噪比增强可以有效提高信号参数测量与调制识别的准确性，但是会影响信号的细微特征，从而降低信号个体识别的可信度。

(3) 对信号质量进行评估，主要包括：脉冲信号的完整性、脉冲多径、脉冲毛刺以及虚假脉冲等。对于低质量的信号可以直接丢弃，将信号质量评估的结果送往下一级。

(4) 根据信号质量调整处理算法进行参数测量以及识别等。

(5) 对于不同的信号质量，给出相应的结果与可信度输出。

本系统采用二阶四阶矩信噪比估计法作为信号的信噪比估计算法。其基本原理是利用信号和噪声的2、4阶矩之间的关系来估计信噪比。二阶四阶矩估计法是一种自适应算法，由于其是基于接收信号的二阶和四阶量估计，从而不需要相位恢复。作为累计量算法，它不需要接收机判决，因此是一种无辅助数据估计算法。在二阶和四阶矩应用于实加性高斯白噪声(AWGN)信道中载波和噪声估计的基础上，可以得出对于实信道和复信道中信噪比估计方法。

假设接收信号与噪声都是零均值、相互独立的随机过程，并且复噪声的同相和正交两路相互独立，则信号的二阶量M2和四阶量M4可以简化表示为：

M2=S+N

(1)

M4=KaS2+4SN+KwN2

(2)

其中：

Ka=E[|an|4]/(E[|an|2])2

(3)

Kw=E[|wn|4]/(E[|wn|2])2

(4)

联立两式可以推出S、N的估计值：

(5)

N=M2-S

(6)

此处S与N的比值即为信噪比。

对于MPSK信号来说，Ka=1；对于复噪声来说，Kw=2，因此可得：

(7)

(8)

在实际应用中，二阶和四阶量是由接收信号的时间平均来计算的，下面给出它们的近似表达式，对于实信道或复信道都适用：

(9)

(10)

式中：N为接收信号时域宽度。

在电磁环境复杂的外场条件下，对实际接收到的脉冲信号，选取信噪比较高的同调制方式、同脉宽脉冲共100个，对常用的3种信噪比估计算法的实际性能和效果进行评估，测试结果如图7所示。由图8可以看出，通过自相关矩阵奇异值分解法与M2M4估计法得出的SNR估计值均低于平方信噪方差比估计法，但是自相关矩阵奇异值分解法的实测SNR估计值略大于M2M4估计法。如图9所示，自相关矩阵奇异值分解法的SNR估计方差在3种算法中是最小的，这表明在信噪比为30 dB左右时，自相关矩阵奇异值分解估计算法的稳定性最佳。

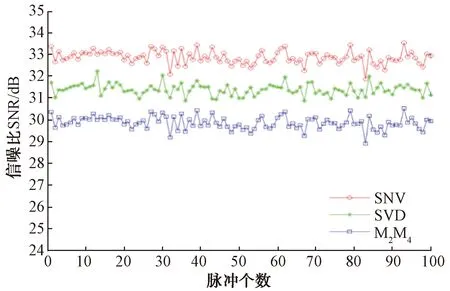
图7 外场条件下3种方法的SNR估计

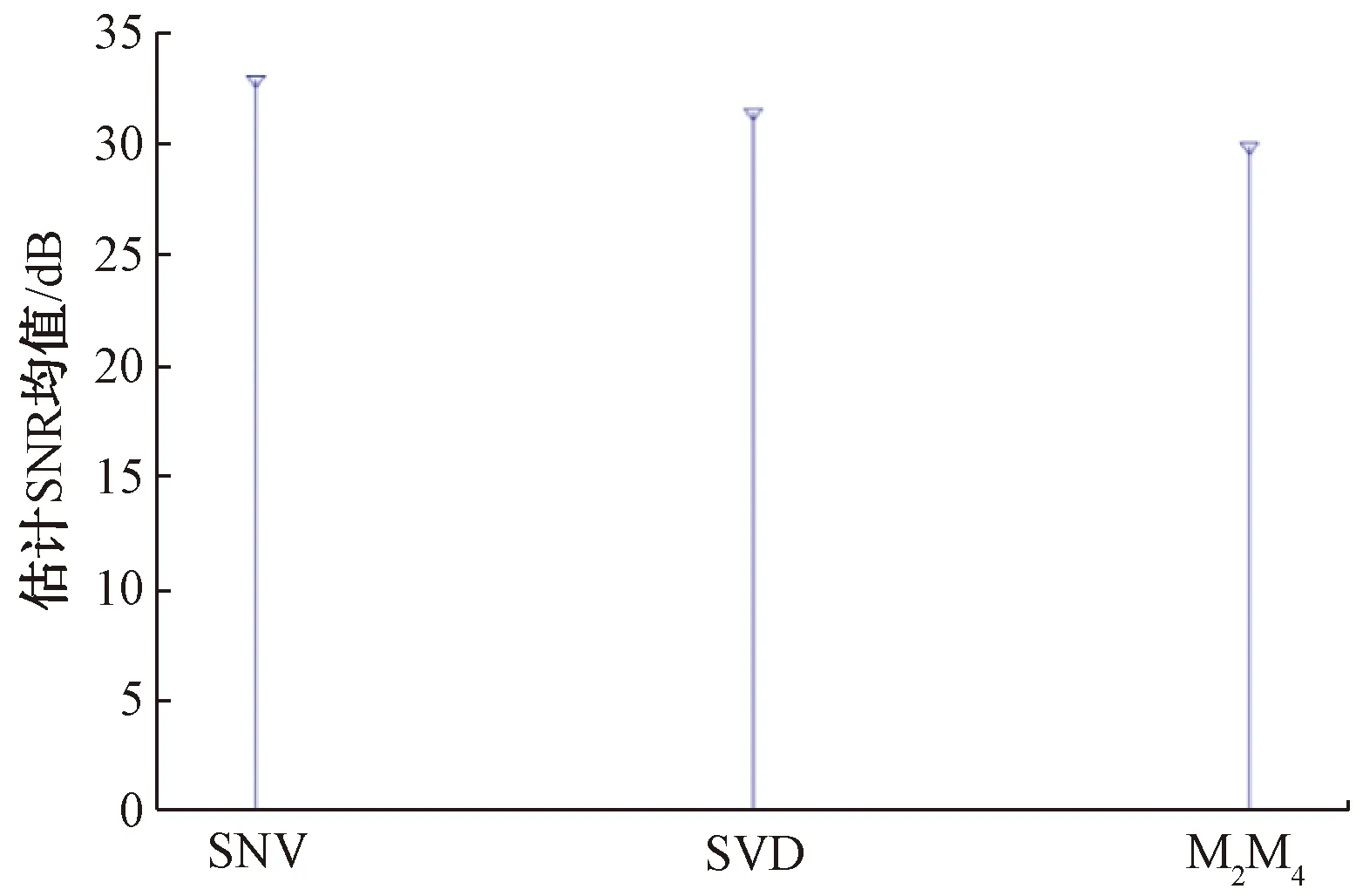
图8 外场条件下3种方法的SNR估计均值

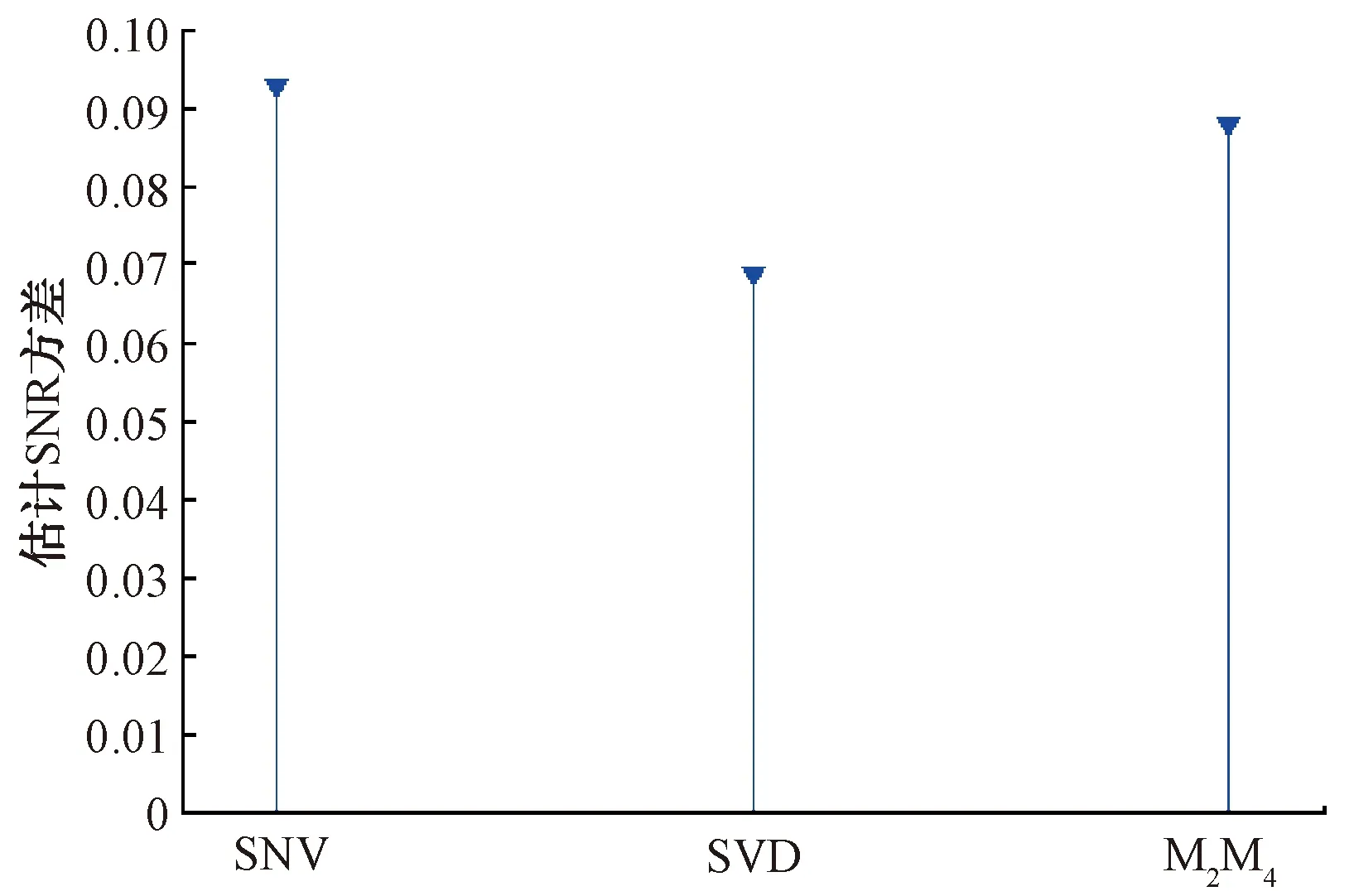
图9 外场条件下3种方法的SNR估计方差

2.3 无模糊相位提取技术

对于接收的的雷达信号，无模糊相位的提取正确性对信号调制方式的准确识别和脉内分析都有很重要的意义。雷达信号模型可以表示为：

r(n)=s(n)+w(n)=Aexp{jφ(n)}+w(n),n=1，…，N

(11)

式中：A为载波幅度；φ(n)为相位；w(n)为方差等于σ2的附加性高斯白噪声；N为样本个数。

由复信号通过反正切可以得到瞬时相位：

(12)

由于测量相位的取值范围为[-π,π]，因此测量相位φ(n)为真实相位，φ对2π取模后的相位值为：

φ(n)=mod(φT(n),2π)

(13)

式中：mod表示取模运算，相位展开算法就是由测量相位解模糊得到真实相位。

等效式为：

φ(n)=φT(n)-kn2π

(14)

式中：kn为第n个样本点所处的周期数，相邻2个样本点之间的相位差为：

Δφ(n)=ΔφT(n)-(kn-kn-1)2π

(15)

在满足奈奎斯特采样定理的情况下，若φT(n)和φT(n-1)处于相邻周期，则Δφ(n)<0,因此可以根据相邻样本点之间的测量相位差逐级解模糊得到信号的真实相位，第n个样本点的真实相位值为：

(16)

当相位被噪声污染时，相邻样本点的相位差为：

Δφ(n)=ΔφT(n)-(kn-kn-1)2π+Δε(n)

(17)

当φT(n)和φT(n-1)处于同一周期内：

Δφ(n)=ΔφT(n)+Δε(n)

(18)

可以看出，当Δε(n)<-ΔφT(n)时，解模糊得到的φT(n)会出现错误。若要降低错误概率，那么ΔφT(n)应该尽可能的大。因为ΔφT(n)∈(0,π]，因此当ΔφT(n)=π时，进行相位展开的性能最佳。图10给出了在0～10 dB信噪比情况下，采样率fs与载频fc比值分别为2,3,5时相位展开错误概率的分布曲线，可以看出采样率fs与fc的比值为2时，错误率最小。

因此，在信噪比较低的情况下，可以通过将采样信号上变频至fs的1/2附近，进行相位展开，得到精确的瞬时相位，再根据上变频的频率求得变频前信号的真实相位。图10为相位展开错误概率的分布曲线。

图10 相位展开错误概率的分布曲线

3 结束语

离线情报分析软件通过采用分层处理架构实现全功能的后处理分析功能，并采用MKL库、OpenMP技术、数据分析并行化等处理加速技术实现了高速离线情报处理；采用信号盲分离解决了信号同时到达分析；通过信噪比估计实现了信号自适应处理，在处理复杂度和处理时间之间取得了平衡；通过无模糊相位提取技术实现了脉内参数测量。通过上述方法，实现了覆盖信号分析、信号分选、情报生成及数据加速的离线情报分析软件，具有功能齐全和性能优越的特点。