无证书的可搜索加密方案

李 双

北京工商大学 数学与统计学院，北京 100048

1 引言

在大数据的今天，为了实现数据的安全性，海量的数据大多加密存储于第三方服务器上，对于这些加密数据的有效检索是一个越来越被人们重视的现实问题。Boneh 等在2004 年利用匿名的基于身份加密方案构造出来第一个公钥可搜索加密方案[1]（Public Key Encryption with Keyword Search，PEKS）。2005年，Abdalla等对可搜索公钥加密方案的一致性进行了重新定义[2]。经过多年的发展，2010年，Kamara和Lauter对构建安全云存储所需的密码原型（包括可搜索公钥加密方案）进行了综述[3]。2012年，Long等提出在全文检索下构建PEKS的方案[4]。2013年，Tseng等提出iPEKS[5]，使得搜索时间是不同关键词的总数的线性关系，而且已搜索得到关键词越多，搜索的效率越高。Hou 等利用“格”构做新的PEKS 算法[6]。2014 年，李等基于属性加密提出的可搜索加密方案[7]，可实现多用户共享查询。2015 年，Xu 等在云存储环境下利用PEKS 构建数据检索系统[8]，采用双系统加密技术减少方案的安全性问题。2017年，Liu等提出双重陷门的基于身份的可搜索加密方案[9]。Shen等把访问控制引入可搜索加密方案[10]。2019年，Jiang等给出关键词可搜索基于身份的广播加密方案[11]，该方案用于数据库系统可以防范内部攻击。同年，Li等提出指定服务器基于身份的用于加密邮件的可搜索认证加密方案[12]。Yin等给出基于密文策略的可搜索加密方案[13]。

2 基础知识

定义1设G1表示素数阶加法群，P为G1的生成元。G2为素数阶乘法群，且它们的阶数相同，记为q。如果映射e:G1×G1→G2满足：

（1）双线性（Bilinear）

对于任意Q,W∈G1和a,b∈Zp，都有：

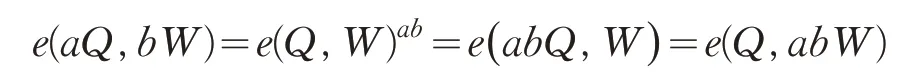
对任意Q,W,Z∈G1，有：

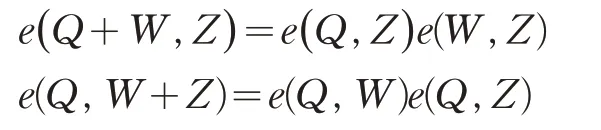
（2）非退化性（Non-degenerate）

存在Q,W∈G1，使得e(Q,W)≠1G2。这里 1G2代表G2群的单位。

（3）可计算性（Computable）

存在有效的多项式时间算法对任意的Q,W∈G1，可计算e(x,y)的值，则称映射e:G1×G1→G2是双线性映射。

定义2设f为f:R→[ ]0,1 上的映射，满足对任意的多项式g(s)和足够大的s，有，则称f为可忽略函数。

下述几个密码学困难问题，将构成无证书可搜索加密方案的安全基础。

计算双线性Diffie-Hellman问题（BDH）：

给定(P,Pa,Pb,Pc)，其中a,b,c∈Zp随机选取且未知,任意算法A计算e(g,g)abc∈G2的优势为ϵ，如果：

判定双线性Diffie-Hellman问题（DBDH）：

给定(P,Pa,Pb,Pc,Q)，其中a,b,c∈Zp随机选取且未知，Q∈G2,P∈G1，任意算法A判断是否Q=e(g,g)abc的优势为ϵ，如果：

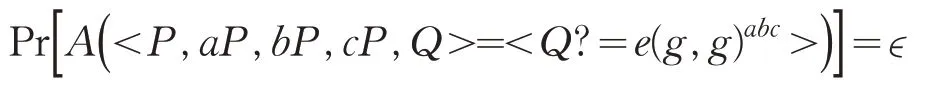
目前尚未有解决计算双线性Diffie-Hellman 问题BDH的有效算法，普遍认为BDH是一个困难问题，即计算和判断双线性Diffie-Hellman问题的优势是可忽略函数。通篇假设双线性Diffie-Hellmen问题（BDH）是难解的。

3 无证书可搜索加密方案的定义

无证书的可搜索加密方案（CL-PEKS）是在基于身份的可搜索加密方案（Identity Based Public Key Encryption with Keyword Search，IBEKS）的基础上结合无证书的加密技术提出来的，在不需要第三方证书认证的情况下，实现对加密数据的关键词的可搜索。

在CL-PEKS 体系中，用户的初始私钥存在密钥生成中心KGC，每个用户根据协议自己计算完整私钥，避免了KGC拥有用户完整私钥的风险。

3.1 CL-PEKS算法定义

定义3无证书的可搜索加密算法CL-PEKS由系统初始化(Setup)、密钥生成(KeyGen)、密钥扩展(KeyExt)、关键词加密(PEKS)、陷门生成(Trapdoor)、验证(Test)多项式时间随机算法组成。

系统初始化(Setup)：输入系统初始参数λ；输出系统公共参数Pub和系统主私钥Msk。Setup 由KGC 来完成，假设系统参数是公开的，可被认证，系统主私钥由KGC秘密保存。

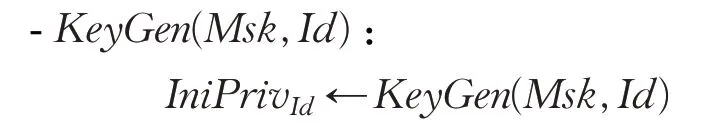
密钥生成(KeyGen)：输入用户身份Id和系统主私钥Msk；输出用户的初始私钥IniPrivId。KeyGen由KGC执行，并将IniPrivId保密传送给用户Id。

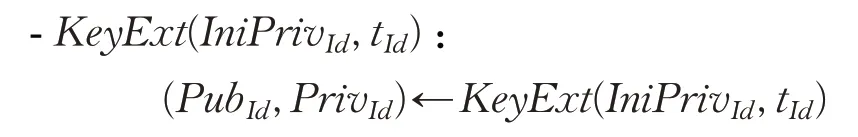
密钥扩展(KeyExt)：输入用户初始私钥IniPrivId和用户随机选取的秘密值tId；输出用户公钥PubId和用户完整的私钥PrivId，并且将公钥PubId以安全的方式发布出去。KeyExt在用户端执行。

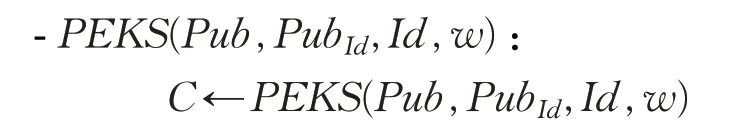
关键词加密(PEKS)：输入系统公共参数Pub和接收方的公钥PubId与身份Id，关键词w；输出查询关键词的密文C。

陷门生成(Trapdoor)：输入用户身份Id，用户完整私钥PrivId和查询关键词w；输出查询关键词w∈{0,1}*的陷门值Tw。

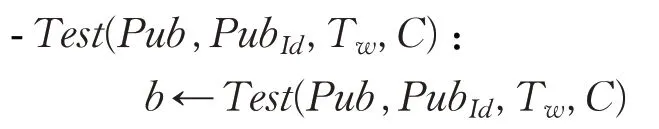
验证(Test)：输入系统公共参数Pub和用户公钥PubId，任何一个查询关键词w′的密文C=PEKS(Pub,PubId,Id,w′)和关键词w的陷门值Tw=Trapdoor(Id,PrivId,w)；输出判断值b。如果b=1，此时判断C是陷门值Tw对应查询关键词w的密文；b=0，此时判断C不是陷门值Tw对应查询关键词w的密文。

对所有的λ∈N，任意关键词，取遍明文空间w∈{0,1}*，全部用户身份Id，取遍用户身份空间，都有：

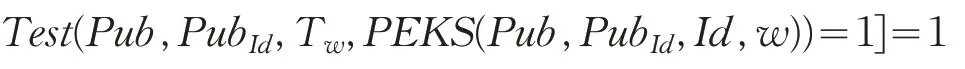
这里：

在CL-PEKS 中每个用户的秘密值tId和完整私钥PrivId由用户独立生成并在本地保管，因此避免了IBEKS中的密钥托管问题。

3.2 攻击游戏

下面讨论无证书可搜索加密方案中的攻击类型，主要涉及两类攻击[14]。

第一种情形：无证书的可搜索加密方案中不存在数字证书，在这种情况下假设敌手可以替换任意用户的公钥，并相应地修改公钥目录，由于没有证书授权CA，上述恶意攻击行为将不会被发现。但敌手无法获取系统主私钥Msk。此过程称为第一种情形攻击。

第二种情形：有一个基本原则敌手在整个攻击过程中不允许替换用户公钥，在此原则下，假设敌手可获知KGC 的主密钥Msk，并可得到用户的全部私钥。此过程称为第二种情形攻击。

攻击过程敌手可以发起下列操作：

（1）敌手请求指定用户初始密钥：挑战者执行算法KeyGen(Msk,Id),输出用户的初始私钥IniPrivId发送给敌手，此处用户身份是敌手选定身份Id。

（2）敌手请求指定用户完整私钥：挑战者执行算法KeyExt(IniPrivId,tId)，得到完整私钥PrivId发送敌手。如果用户Id的公钥被替换过，则游戏结束。

（3）敌手请求指定用户公钥：挑战者运行KeyExt(IniPrivId,tId)，得到用户Id的公钥PubId回应敌手。同时挑战者在本地保存敌手请求过的公钥PubId-list[(PubId,tId)]表。

（4）敌手替换指定用户公钥：用新的公钥Pub′Id替换用户Id的公钥PubId。

（5）敌手请求关键词w的陷门：如果用户Id的公钥PubId被替换过或者PubId没有出现在PubId-list中，则游戏终止；否则挑战者执行KeyExt(IniPrivId,tId)，得到用户Id的完整私钥PrivId，生成关键词w的陷门Tw。

针对第一种情形攻击的几点约束：

（1）敌手任何时刻都不能获得挑战者的私钥；

（2）敌手不可请求某些用户的私钥，如果这些用户的公钥已经被替换过；

（3）敌手在挑战阶段之前不能替换挑战者的公钥，在某些时期不能请求获得挑战者的初始私钥；

（4）在第二阶段敌手不能请求使用挑战者私钥生成的关键词陷门。

针对第二种情形攻击的几点约束：

（1）敌手任何时刻都不能替换公钥；

（2）敌手不能请求获得挑战者的私钥；

（3）在第二阶段敌手不能请求使用挑战者私钥生成的关键词陷门。

上述约束条件贯穿整个攻击过程。

敌手与挑战者间进行如下游戏：

初始化阶段：挑战者输入系统参数λ，执行算法Setup(1λ)输出系统公共参数Pub并发送给敌手，如果敌手是第一种情形，挑战者将系统主私钥Msk秘密保存；如果敌手是第二种情形，挑战者将系统主私钥Msk发送给敌手。

第一阶段：敌手可以向挑战者作一系列q1,q2,…,qn次请求，可以获得指定用户的初始私钥、全部私钥、公钥、替换公钥、生成关键词陷门的请求。如果攻击是第二种情形，不允许敌手替换指定用户公钥。

挑战阶段：当敌手决定第一阶段终止，敌手发送挑战者身份IdCh，关键词w0,w1，请求得到关键词w0,w1的密文。要求挑战者IdCh不可以是已经被敌手请求得到其私钥的用户身份。如果攻击属于第一种情形，挑战者不能是已被替换公钥或者已被请求得到其初始私钥的用户身份。满足条件挑战者随机选取b∈{ }0,1 ，执行算法C*=PEKS(PubIdChIdCh,wb)并发送关键词密文给敌手。

第二阶段：敌手继续向挑战者做一系列新的请求qn+1,…,ql。特别地，敌手不允许请求挑战者IdCh的私钥，如果属于第一种情形攻击，当挑战者IdCh的公钥在第一阶段已被替换，此时不允许敌手请求获得挑战者IdCh的初始私钥，敌手只允许请求获得第一阶段没有请求过的关键词w的陷门。对于第二种攻击情形，不允许敌手替换指定用户公钥。

猜测阶段：敌手输出猜测结果b′∈{ }0,1 。如果b′=b，则敌手赢得比赛。

定义4对于两种情形不可区分选择密文攻击（INDCCA2）的优势函数为：

其中λ是系统安全参数。

定义5对任意多项式时间攻击敌手破译CL-PEKS的优势是可忽略函数，则称CL-PEKS是选择关键词密文攻击语义上安全的。

4 算法构造

4.1 CL-PEKS算法构造

构造的无证书的可搜索加密方案CL-PEKS，采用了Terada的无证书公钥密码算法（CL-PKE）[15]中无证书的技术。设，其中q是群的阶数为素数。e:G1×G1→G2是一个双线性映射，选取有限域上椭圆曲线的Weil pairing 或者Tate分别是哈希函数，这里 0 ＜k＜n都是整数，CL-PEKS 由以下多项式时间算法构成：

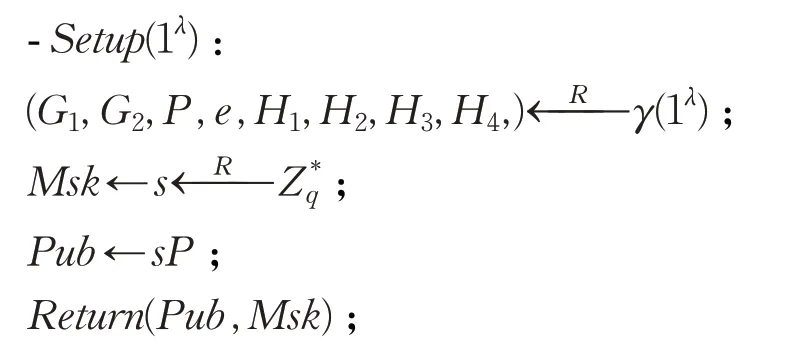
系统初始化：这一步在密钥生成中心KGC 执行。输入系统初始化参数λ，随机选取s∈；输出系统随机选取的椭圆曲线上加法群G1,G1=P，P是G1生成元，系统的主公钥Pub=sP和主私钥Msk=s。

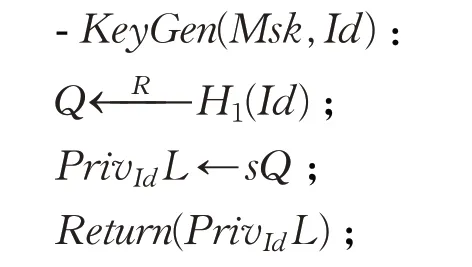
密钥生成：KGC运行算法KeyGen。输入系统主私钥用户身份Id；输出用户的初始私钥PrivIdL=sQ。

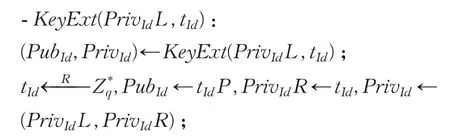
密钥扩展：用户Id在本地运行算法KeyExt。输入用户初始私钥PrivIdL，随机选取tId∈并于用户本地秘密保存；输出用户公钥PubId=tIdP，用户完整私钥PrivId←(sQ,tId)。这步由用户来完成，完整私钥存储于用户本地，用户公钥PubId通过安全方式发送给KGC，由KGC发布出去。

关键词加密：KGC运行算法PEKS。输入系统公共参数Pub，用户身份Id，公钥PubId和查询关键词w；输出查询关键词的密文C。预处理需要计算gr=查询关键词密文是一个四元组，C=rP,rQ,lP,(H4(t)||σ)⊕H2(rP,gr,lP)的计算式中“⊕”表示直和，其中σ∈{0 ,1}k是随机数，H1(w),H4(t)分别是对应的哈希函数，“||”表示连接。

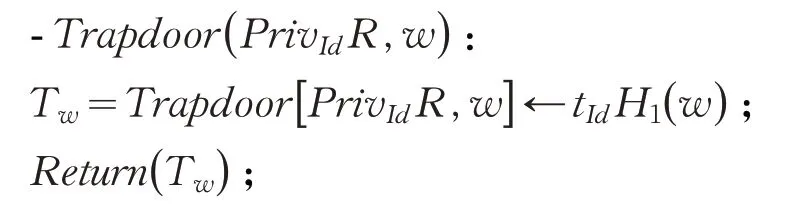
陷门生成：查询用户运行Trapdoor。输入用户私钥的秘密部分PrivId和查询关键词w；输出查询关键词的陷门Tw=tIdH1(w) 。

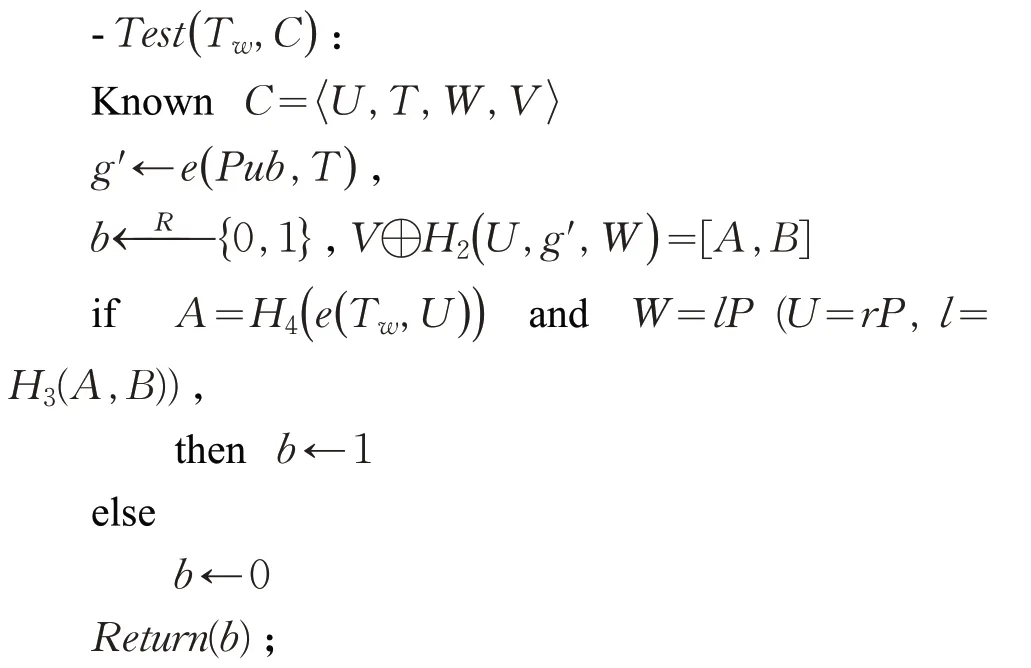
验证：服务器运行算法Test。输入查询关键词密文C和关键词w的陷门值Tw，输出判断值b。

具体计算过程如下。

首先计算：

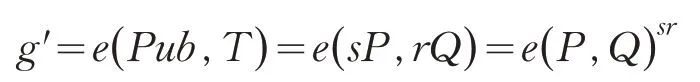
V⊕H2(U,g′,W)，计算结果的前n-k比特是A，后k比特是B。由A和B可计算l=H3(A,B)，接下来验证等式W=lP和A=H4(e(Tw,U))是否成立，输出“1”表示“关键词密文和关键词陷门对应同一查询关键词”；输出“0”表示“关键词密文和关键词陷门对应不同查询关键词”。此过程服务器无法获知查询关键词的明文。

本文构造的CL-PEKS不仅实现了对于加密关键词的可搜索性，由于引入无证书的技术，避免了基于身份的可搜索加密方案（IBEKS）中用户私钥完全暴露给KGC的风险。

4.2 CL-PEKS一致性分析

利用有限域椭圆曲线Weil pairing双线性性质：

4.3 CL-PEKS复杂度分析

这里分别比较无证书公钥密码算法CL-PKE[15]、基于身份的可搜索加密方案CL-IBEK4.1、关键词可搜索公钥加密方案PEKS[1]，如表1，三种密码方案在进行加密/（Crypt/PEKS）、解密/验证（Decrypt/Test）、陷门（Trapdoor）的计算过程中涉及的双线性对运算（P）、椭圆曲线群中的纯量乘法（M）、指数运算（E）、哈希函数（H）四种运算次数；以及公钥（Pub）、消息/关键词明文（M/w）、消息/关键词密文（Ciph）、关键词密文（Tw）的二进制表示比特数。这里假设哈希函数H2的输出二进制表示的比特数为n,g表示G1中点的二进制表示的比特数。

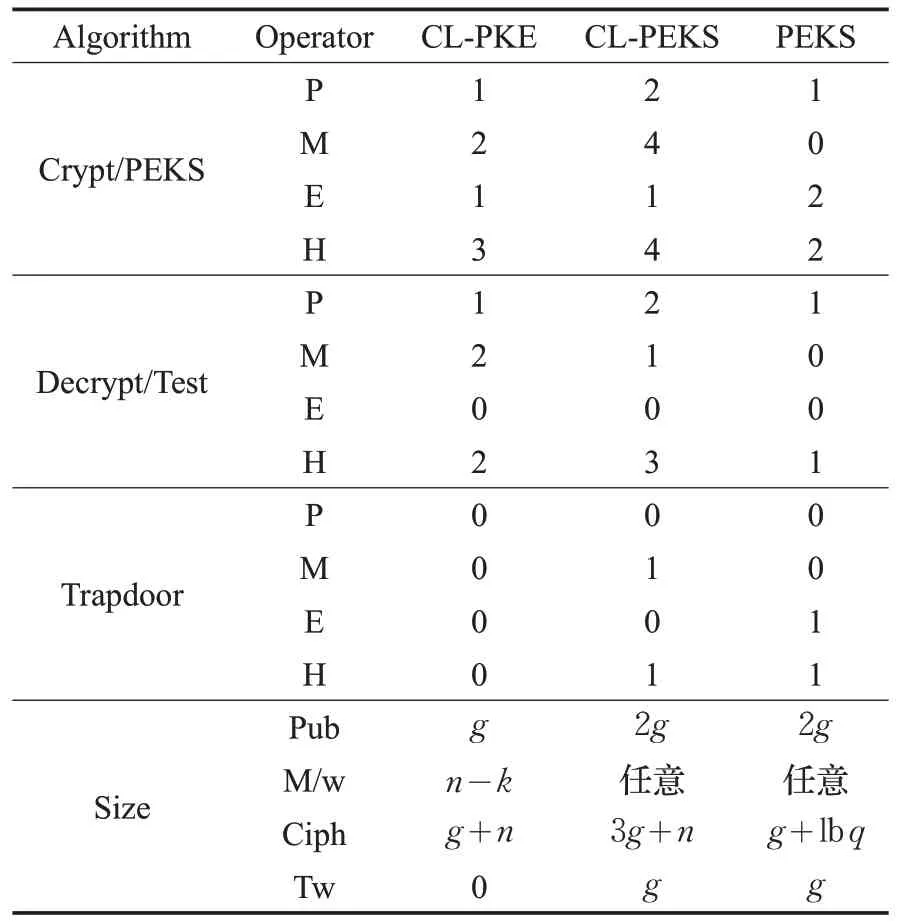
表1 CL-PEKS运算量统计表

这里将CL-PEKS4.1与CL-PKE[15]进行比较，可以看出CL-PEKS与CL-PKE的计算量基本相当，并且实现了无需证书的对加密关键词的可搜索功能，省去了CA认证环节，避免了密钥托管等问题。

5 结论

给出CL-PEKS 的定义、算法构造以及算法的计算一致性和算法复杂度分析。算法的安全性基于BDH和GDH 等密码学难题。因此，提出的CL-PEKS 方案具有对加密关键词的检索功能，解决了IBEKS方案中的密钥托管问题。CL-PEKS方案还仅仅只是一个基础的原型方案，随后还会继续深入探索该模型在随机预言机模型下的安全性等问题。