预应力混凝土连续刚构桥模糊综合评估法研究
王红伟,谢开仲
(1. 广西新发展交通集团有限公司,广西 南宁 530029;2. 广西大学 土木建筑工程学院,广西 南宁530004;3. 广西大学 防灾减灾与工程安全重点实验室,广西 南宁530004)
预应力混凝土(Prestressed Concrete,简称PC)连续刚构桥在荷载、外界腐蚀因素等影响下,会出现各种病害[1-3],威胁结构安全性[4-5],准确高效评估其状态具有重要意义[6]。目前,针对PC连续刚构桥的状态评估研究,监测数据的获取与存储[7]、新型监测设备与技术[8]的应用发展比较迅速,但监测数据的利用率不高[9],根据监测数据评估PC连续刚构桥的状态发展比较缓慢[10],亟需开展深入研究。国内学者提出了不同的方法和模型,例如王佶等[11-18]这些学者多是考虑多种因素影响,将层次分析法与某种具体理论结合起来,建立PC连续刚构桥的状态评估模型,并与实桥测试进行验证对比,评估体系比较明确,有力地促进了PC连续刚构桥状态评估技术的发展。但不同学者的评估体系指标、指标的评判标准、权重的处理方法以及考虑的因素等各有差异,由于PC连续刚构桥承载力影响因素多,关于PC连续刚构桥状态评估体系的指标构成以及指标的评判标准,目前工程界和学术界还没有统一的标准,有待深入开展研究。为此,本文在现有研究的基础上,针对PC连续刚构桥的结构和受力特点,提出基于层次分析法和模型综合评估方法相结合的PC连续刚构桥状态评估方法,建立了PC连续刚构桥的状态评估体系,确定了评估体系中各个指标的评判标准和权重,并采用实桥测试验证了方法的可行性。
1 状态评估体系建立
在前人研究工作基础上,对PC连续刚构桥状态评估影响因素进行筛简[19],建立了PC连续刚构桥的状态评估体系,见图1。
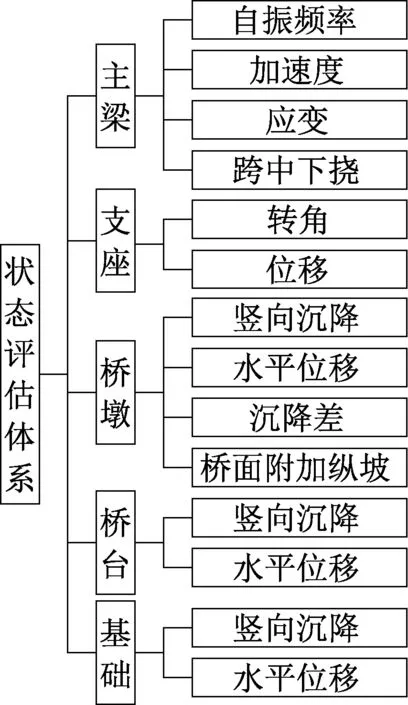
图1 PC连续刚构桥的状态评估体系
2 指标评判标准建立
在现行规范和前人研究工作的基础上,根据评估指标的状态及其对桥梁安全性的影响程度,将其分成优、良、中、差、危险共五种状态,并制定指标的评判标准。为了对比不同类型指标,将底层指标无量纲化处理,优、良、中、差和危险对应无量纲化分值分别为[0.8,1]、[0.6,0.8)、[0.4,0.6)、[0.2,0.4)和[0,0.2)。本文主要从上部结构、支座和下部结构三部分建立指标的评判标准。
2.1 上部结构
根据主梁的受力状态及其影响因素,将其评判指标分为跨中下挠、应变、自振频率和加速度四个部分,具体评估标准如下。
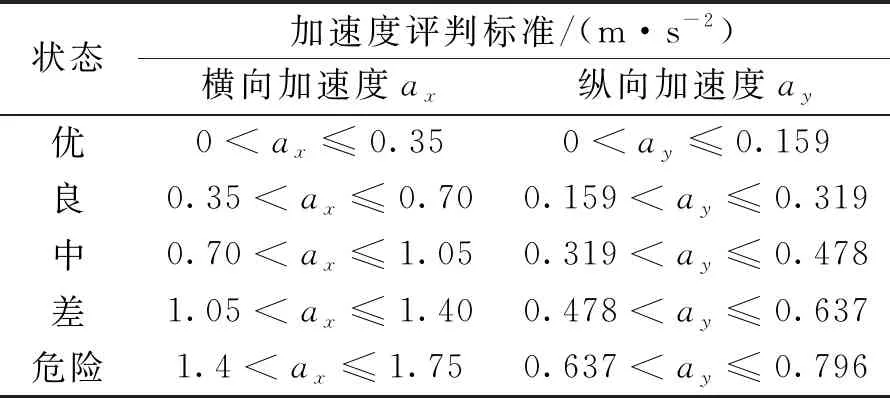
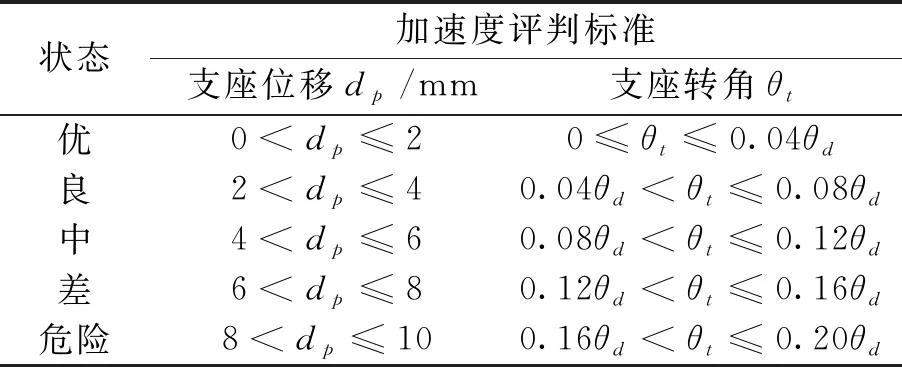
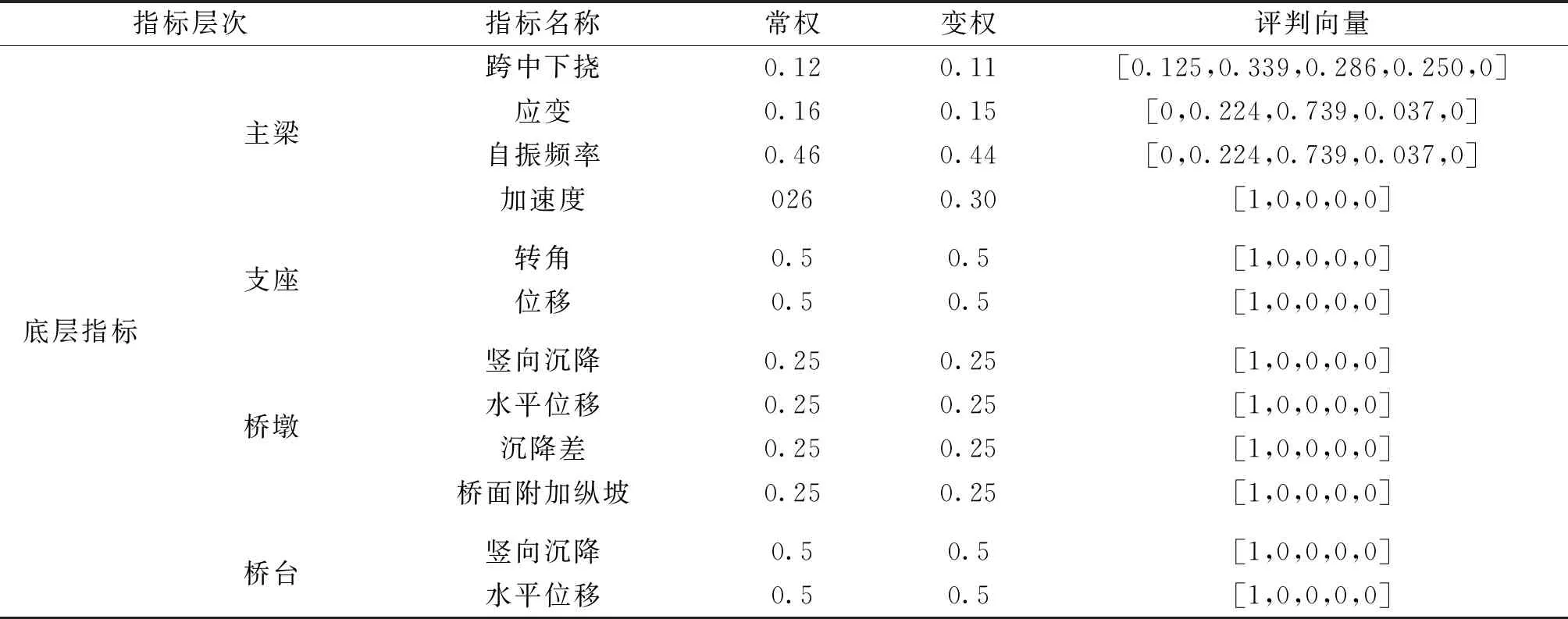
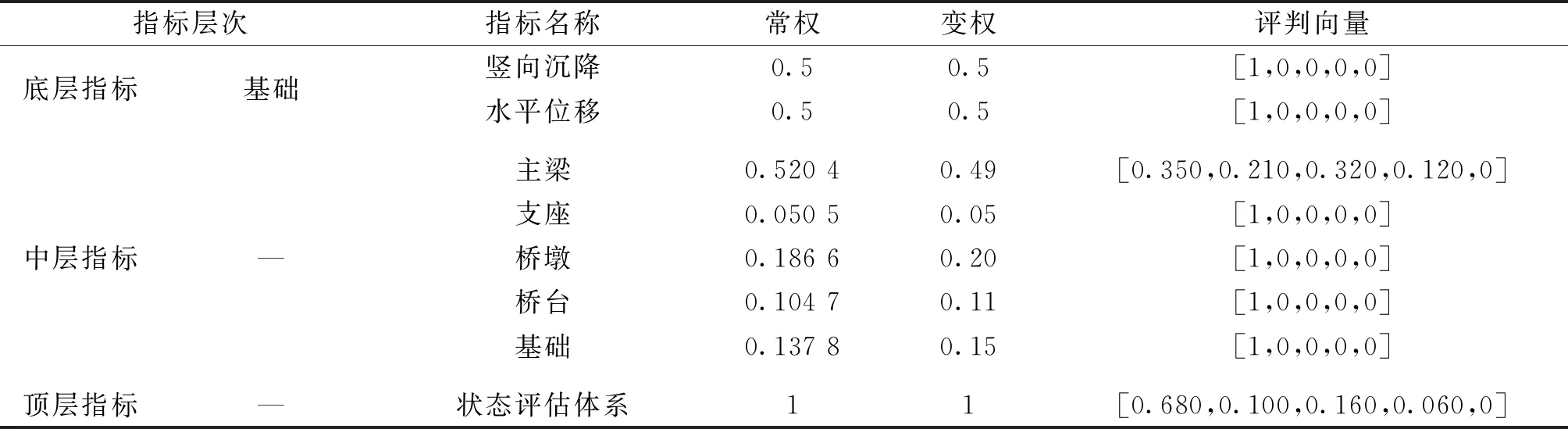
(1)跨中下挠。基于2011版桥梁技术状况评定标准,结构PC连续刚构桥的受力特性和病害特征,将跨中最大挠度和计算跨径分别记为Dmid(m)和L(m),优、良、中、差、危险分别对应评判标准为Dmid≤L/3 000、L/3 000 (2)应变。应变ε能够反映PC连续刚构桥的受力状态。混凝土开裂或压碎后可认为是退出工作状态,以ε达到材料拉压强度设计值和0分别作为危险和良好的上限,线性内插确定其它状态。 (3)自振频率。参照规范[20]将自振频率评估标准分为五个区间。 (4)加速度。加速度也是PC连续刚构桥的重要动力指标。基于2004版铁路桥梁检定规范和加拿大Ontario桥梁规范中加速度的限值规定,将横向和竖向加速度分别记为ax(m/s2)和ay(m/s2),横向和竖向加速度不同状态的评判标准见表1。 支座评判指标包含位移和转角两部分。将支座位移记为dp(mm),支座转角的设计值与实 表1 加速度的评判标准 测值分别记为θd和θt。基于现行桥梁技术状况评定标准和支座设计规范,结合支座的受力特性和病害特征,支座位移和转角不同状态的评判标准见表2。 表2 支座位移和转角的评判标准 包括桥墩、桥台和墩台基础三部分,基于现行的2011版公路桥梁技术状况评定标准,结合桥墩、桥台和基础的受力特性和病害特征,具体评判标准如下。 PC连续刚构桥状态影响因素多且复杂,这些因素的影响水平也处于模糊状态,利用模糊理论能够较好地解决PC连续刚构桥的状态评估。模糊理论在数学上已经比较成熟,包括集合定义、运算法则、主要算子和隶属函数等,此处不再详述。为了高效构建模糊集合和确定评估结果,基于指派法选择梯形和半梯形的隶属函数,见图2。应用模糊综合评估的步骤见图3。 图2 隶属函数 图3 模糊综合评估的主要步骤 利用模糊评估方法进行PC连续刚构桥状态评估时,首先采用层次分析法建立大跨度PC连续刚构桥的评估体系,其次确定指标评判标准和隶属函数,最后由下向上逐层评估,主要步骤见图4。 图4 PC刚构桥中模糊综合评估的主要步骤 (1)求解底层指标的常权。基于各指标相对重要性程度建立矩阵Bk,矩阵Bk中元素bij表示指标bi对指标bj的重要性程度,分为相同——1分、偏强——3分、较强——5分、强烈——7分和极端——9分,共计5个等级,且矩阵中元素满足bij>0,bii=1,bij×bji=1。 求解Bk的最大特征值λmax和对应特征向量Amax。 计算矩阵的CR值,检验矩阵的一致性,若CR<0.1,则权重值合理,若CR≥0.1,需调整bij值。 将Amax归一化可得指标常权值。 CR=(λmax-n)/[(n-1)×RI] (1) 式中:CR为随机一致性比率;RI为随机一致性指标;n为矩阵的阶数。 (2)求解底层指标的变权。针对常权存在的问题:个别危及桥梁安全性的局部严重损坏不能有效反映在整体评估结果中,引入变权公式(2)计算变权值。 ωj(v1,v2,…,vn)= (2) (3)求解中层指标的常权与变权。中层与底层指标的常权与变权求解方法同理,此处省略。 (1)求解底层指标的评判向量。基于底层指标评判标准,由底层指标的实测值和理论值可得底层指标分值,将底层指标分值代入隶属函数中可得底层指标评判向量,将底层指标评判向量组成评判矩阵,最后将评判矩阵按行归一,按列求和再归一,可得底层指标的评判向量。 (2)求解中层和顶层指标的评判向量。中层和顶层指标的评判向量均是通过判断矩阵与权重向量进行模糊运算M(·,⊕)获得。针对顶层指标的评判向量,采用加权平均法得出PC刚构桥总体得分和状态等级。 钦江三桥主桥为三跨PC连续刚构桥,采用双薄壁墩和明挖扩大基础。钦江三桥主桥立面布置示意图见图5。 图5 钦江三桥主桥立面布置示意图 采用荷载试验方法针对钦江三桥开展静载和动载试验,基于静载和动载试验数据的分析,结果表明钦江三桥的静力和动力性能均满足规范要求,桥梁性能处于优秀等级。 基于钦江三桥的荷载试验数据,采用文中提出的PC连续刚构桥状态评估方法,对钦江三桥的健康状态进行评估,具体结果见表3。由加权平均原则可得钦江三桥状态为优(0.88分),与荷载试验结果一致。 表3 钦江三桥健康状态评估结果 表3(续) 1)采用层次分析法建立的PC连续刚构桥状态评估体系和指标评判标准能够有效地反映PC连续刚构桥的受力特点和结构状态。 2)提出的PC连续刚构桥模糊综合评估方法以及指标权重和评判向量的计算方法,能够有效地计算和获取PC连续刚构桥的健康状态。 3)采用提出的模糊综合评估方法对钦江三桥进行状态评估,结果表明钦江三桥的得分为0.88,健康状态为“优秀”,与荷载试验结果相符。2.2 支座
2.3 下部结构
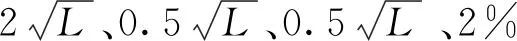
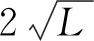
3 模糊综合评估法
3.1 模糊综合评估步骤
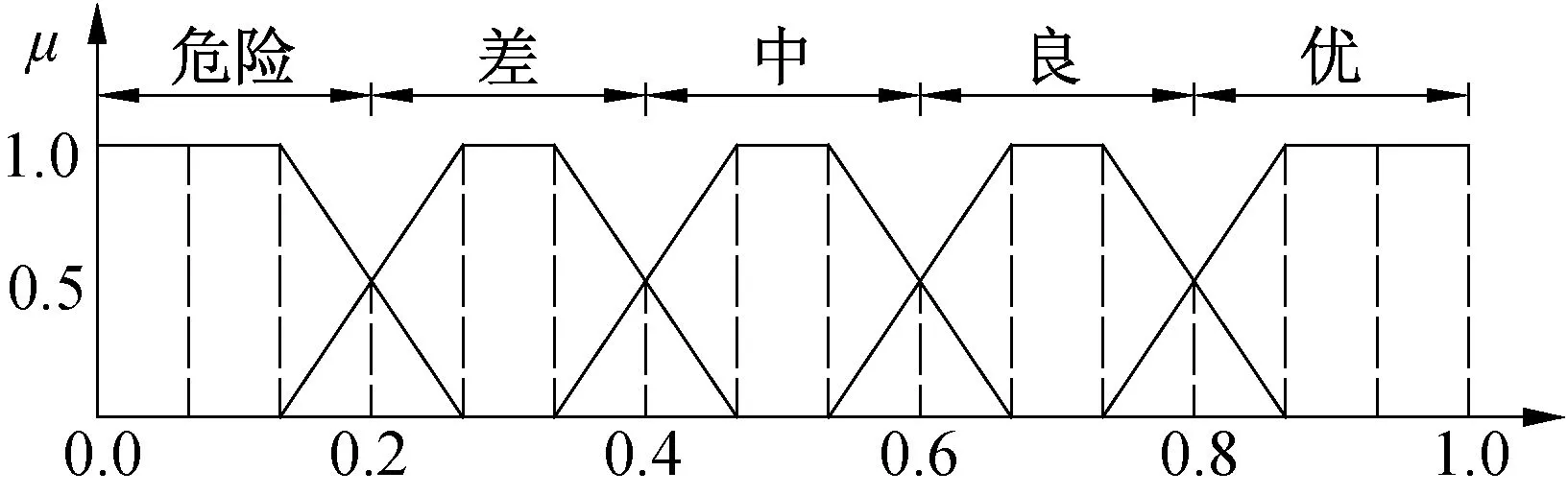
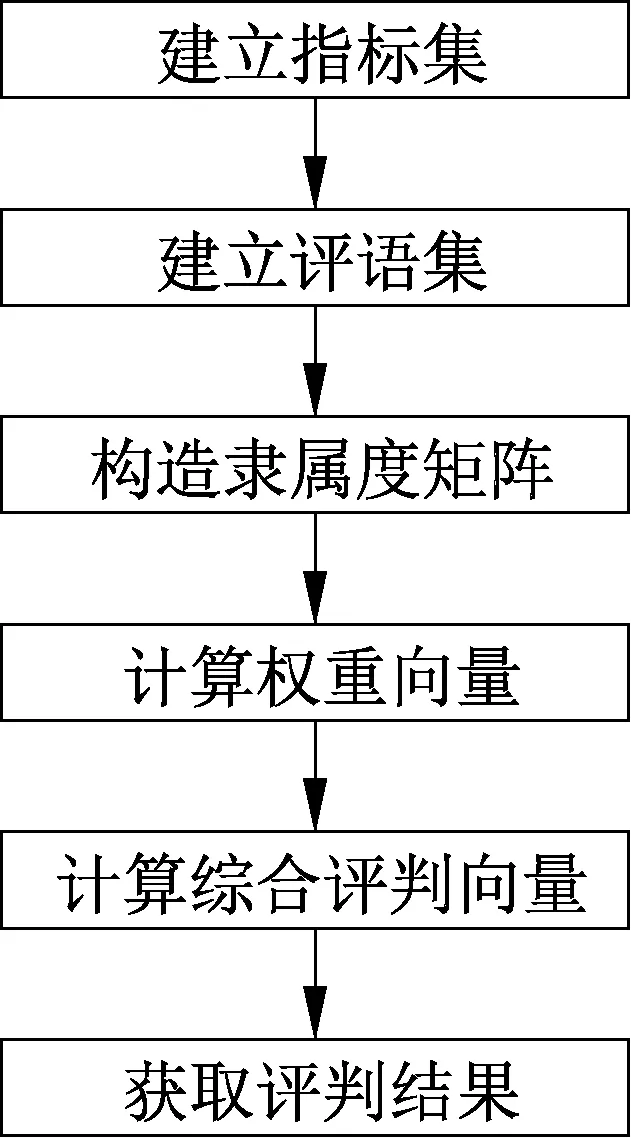
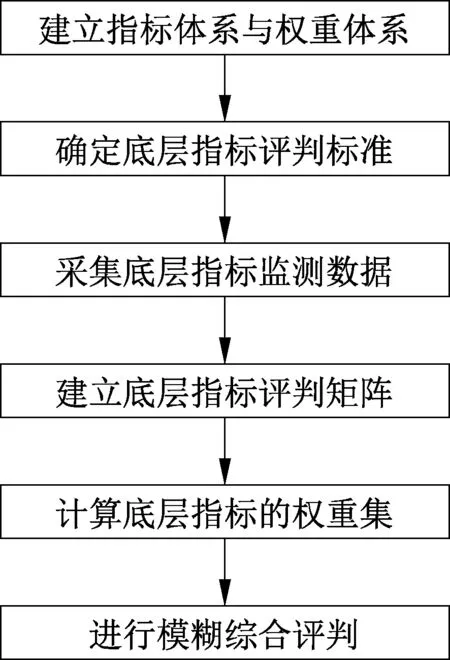
3.2 状态评估体系指标权重的求解
3.3 状态评估体系指标评判向量的求解
4 工程实例
4.1 工程概况

4.2 状态评估结果
5 结论

